Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Агашина М.А. 1 Фищев С.Б. 1 Лепилин А.В. 2 Дмитриенко С.В. 3 Балахничев Д.Н. 1 Орова И.В. 1 Севастьянов А.В. 1

---

1 ФГБОУ ВО «Санкт-Петербургский государственный педиатрический университет» Минздрава РФ

2 ФГБОУ ВО «Саратовский государственный медицинский университет им. И.В. Разумовского» Минздрава РФ

3 Пятигорский медико-фармацевтический институт – филиал ФГБОУ ВО «Волгоградский государственный медицинский университет» Минздрава РФ

Статья в формате PDF

0 KB

1. Бердин В.В., Севастьянов А.В., Фищев С.Б., Дмитриенко Д.С., Лепилин А.В. К вопросу определения размеров зубных дуг в сагиттальном и трансверзальном направлениях. // Стоматология детского возраста и профилактика. – 2013. – Т. ХII – № 3(46). – С. 43–45.

2. Романовская А.П. Антропометрический метод оценки гармонии лица // Проблемы, достижения и перспективы развития медико-биологических наук и практического здравоохранения. – Труды КГМУ. – 2002. – Том 138, ч. 1. – С. 167–170.

3. Севастьянов С.Б., Фищев И.В., Орлова и др. Определение расположения постоянных зубов в зависимости от размера на ортопантомограммах.. // Стоматология детского возраста и профилактика. – 2014. – Т. ХIII – № 4 (51). – С. 48–50.

4. Фищев С.Б., Севастьянов А.В., Дмитриенко Д.С., Бердин В.В., Лепилин А.В. Основные линейные параметры зубочелюстных дуг при нормодонтизме постоянных зубов. // Стоматология детского возраста и профилактика. – 2012. – Т. ХI – № 3(42). – С. 38–42.

5. Фищев С.Б., Севастьянов А.В., Орлова И.В., Королёв А.И., Багомаев Т.С. Эффективность компьютерного моделирования результатов лечения пациентов с дефектами зубных рядов в сочетании с с дистальной окклюзией. // Стоматология детского возраста и профилактика. – 2015. – Т. XIV. – № 1 (52). – С. 23–28.

6. Bolton W.A. The clinical application of a tooth-size analysis. // Am. J. Orthod., 1962. – № 48. – Р. 504–529.

7. Gesch D., Kirbschus A., Gedrange T. Do bivariate and multivariate cephalometric analyses lead to different results concerning the skeletal cause of postnormal occlusion? // Funct Orthod. 2005 Summer-Fall;22(2):6-8, 10, 12-13.

8. Poosti M., Jalali T. Tooth size and arch dimension in uncrowded versus crowded Class I malocclusions. // J. Contemp. Dent. Pract. – 2007. – № 8(3). – Р. 45–52.

9. Potter R.H., Nance W.E. A twin study on dental dimension. I, Discordance, asymmetry and mirror imagery // Am. J. Phys. Antropol. – 1976. – № 44. – P. 391–395.

10. Potter R.H., Nance W.E. A twin study on dental dimension. II, Independent genetic determinants // Am. J. Phys. Antropol. – 1976. – № 44. – P. 397–412.

11. Tanaka M.M., Johnson L.E. The prediction of the size of unerupted canins and premolars in a contemporary orthodontic population. JADA 88: 798-801. – 1974.

В работе определена взаимосвязь линейных параметров зубной дуги нижней челюсти. Представлены ориентиры для определения зубной дуги нижней челюсти, а также обоснование определения размеров зубной дуги нижней челюсти.

Основным фактором, определяющим положение зубов в зубном ряду является соответствие размеров зубов параметрам зубных дуг [1, 3, 4, 10].

Особое внимание в клинической практике уделяется форме и размерам зубных дуг [6, 7]. Основным параметром зубной дуги является ее длина. Анализ лонгитудинальной длины зубных рядов был предложен Nance (1947). При этом длина зубной дуги (от дистальной поверхности первого постоянного моляра до дистальной поверхности антимера) соответствует мезиально-дистальным диаметрам коронок зубов, составляющих зубной ряд [8, 9]. В последнее время широко используется метод Bolton (1962), в основе которого лежит анализ соответствия между12 верхними и нижними зубами, рассчитанные по предложенным формулам [5]. В последнее время многие специалисты указывают на объективность применения метода Болтона, для анализа взаимоотношений между параметрами зубных дуг и размерами зубов [2, 7, 11].

Параметры зубных дуг определяются в различных направлениях. В трансверсальном направлении предложены методы Пона, Линдер-Харта. В сагиттальном направлении – метод Коркхауза. Равенство сегментов зубных дуг было отмечено Герлах [2]. Идеальная модель зубных рядов, по мнению специалистов, имеет следующие признаки: плотные окклюзионные контакты зубов; отсутствие ротации зубов; специфическая инклинация и ангуляция зубов; ровная окклюзионная плоскость и избыток свободного пространства [4].

Для формирования зубных рядов большое значение имеет мезиально-дистальный диаметр коронок зубов. Мезиально-дистальный диаметр коронок определяется преимущественно генетическими факторами. Этот параметр является стабильным и практически, с возрастом не изменяется. В то же время апикальная и альвеолярная части челюстных костей адаптивна и компенсаторная по своей природе [4].

Анализ формы и размеров зубных дуг нередко проводят по методу Хаулея-Гербера-Гербста [2]. Однако основным ориентиром для построения геометрически-графической репродукции авторы рекомендуют использовать сумму мезиально-дистальных диаметров медиального, латерального резцов и клыка верхней челюсти. В то же время отмечена вариабельность размеров латеральных резцов, вплоть до их полной редукции.

Заслуживает внимание изучение размеров зубных дуг по геометрически-графической репродукции с использованием бета-функции по формуле S. Braun, 1998:

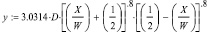
где D – глубина зубной дуги, W – ширина зубной дуги в области вторых моляров, X – ширина зубных дуг на исследуемом уровне, Y – глубина зубной дуги на исследуемом уровне (рис. 1).

Данная методика позволяет определить размеры в любом участке верхней зубной дуги. Однако для ее построения необходимо знать ширину и глубину зубной дуги в области вторых постоянных моляров. К тому же в данной методике не нашли отражения такие параметры как длина зубной дуги и размеры зубов, составляющих зубной ряд.

Все вышеизложенное предопределило цель настоящего исследования, а именно определение параметров зубных дуг нижней челюсти по размерам зубов, составляющих зубной ряд.

Лонгитудинальную длину зубных рядов определяли по методу Nance, как сумму мезиально-дистальных диаметров от второго моляра нижней челюсти до медиального резца. Зубы мудрости не включали в измерения, как наиболее вариабельные. Несмотря на то, что, по мнению Potter R.H. (1976) индивидуальные размеры противоположных квадрантов одной зубной дуги имеют довольно высокий коэффициент корреляции (0,9), встречаются односторонние аномалии размеров зубов (макро- и микродонтизм ), которые могут изменять форму и размеры зубных дуг, что имеет важное значение при определении симметричности обеих половин зубной дуги. В связи с этим нами предложено измерять зубную дугу (L) в отдельности для правой (d) и левой (s) половин зубной дуги нижней челюсти. При нормодонтизме постоянных зубов Ld = Ls и зеркально соответствовали друг другу (рис. 2).

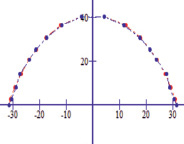
Рис. 1. Геометрически графическая репродукция зубной дуги, построенная с учетом бета-функции

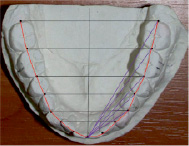
Рис. 2. Фотография модели нижней челюсти с нанесенными реперными линиями для определения основных параметров

Длину зубной дуги считали основным параметром для определения глубины (D), ширины (W) и фронтального диагонального размера (F) зубной дуги. Опытным путем определена константа для определения фронтального диагонального размера зубной дуги для жевательных зубов (KFж), которая составляла 1,1, для клыков (KFк) – 1,06 и для латеральных резцов нижней челюсти (KFр) – 1,03 Таким образом, фронтальная диагональ, соединяющая точки зубной дуги, соответствующие расположению медиальной поверхности медиального резца нижней челюсти и середине дистальной поверхности второго постоянного моляра, равнялась отношению длины зубной дуги (Ld или Ls), к константе фронтального диагонального размера зубной дуги (KFж).

Ширина зубной дуги между вторыми молярами коррелировала с длиной зубной дуги. Опытным путем определена константа для определения ширины зубной дуги между вторыми постоянными молярами (KW), которая составляла 2,07.

Зная размеры фронтальной диагонали и ширину дуги, глубина зубной дуги (D) рассчитывалась по формуле:

D = √F² – (W/2)².

При нормодонтизме и соответствии размеров зубных дуг (полу дуг) верхней челюсти левой и правой размеры полученных дуг зеркально соответствовали друг другу.

Полученные данные легли в основу определения параметров зубной дуги в любой исследуемой точке (х).

Во-первых, определяли длину фронтальной диагонали. Для жевательных зубов она определялась по формуле:

F_x = L_x / (KF_ж).

Для клыков:

F_x = L_x / (KF_к).

Глубину зубной дуги в искомой точке определяли по формуле:

D_x = D – (F – F_x).

Ширину зубной дуги в искомой точке (Wx) определяли по формуле:

W_x = v F_x ² – D_x ².

Ширину зубной дуги в искомой точке (Wx) рекомендуем рассчитывать с учетом известных параметров, а именно, в зависимости от длины и глубины зубной дуги в области вторых постоянных моляров.

Ширину зубной дуги в искомой точке (Wx) для моляров и премоляров определяли по формуле:

W_x = v (L_x / 1,1)2 – (D – L + L_x)².

Ширину зубной дуги в искомой точке (Wx) для клыков определяли по формуле:

W_x = v (L_x / 1,06)2 – (D – L + L_x)².

Ширину зубной дуги в искомой точке (Wx) для латеральных нижних резцов определяли по формуле:

W_x = v (L_x / 1,03)2 – (D – L + L_x)²,

где D – глубина зубной дуги до вторых моляров;

L – длина зубной дуги до вторых моляров;

L_x – длина зубной дуги до искомой точки.

Для удобства измерений нами предложено использовать компьютерные программы для анализа размеров зубной дуги верхней челюсти в различных ее участках, что имеет значение для диагностики и выборе методов ортодонтического лечения.

Библиографическая ссылка