В периодических изданиях тема «Четырехугольники» встречается часто. Содержание научно-методической литературы последних трех лет раскрывает преимущественно вопросы решения и построения четырехугольников [1, 2]. Достаточное количество статей (например, [3]) посвящается вопросам конструирования уроков различных типов, посвященных изучению видов четырехугольников. Анализируя различные научно-методические статьи [1–3], заключаем, что в последнее время авторы все чаще обращаются к данному содержанию в аспекте подготовки обучающихся к итоговым экзаменам. В статье В.Б. Дроздова [2] приводятся выводы известных формул для вписанных четырёхугольников и трапеций. В работе С.М. Тахаева [1] проведен анализ четырёхугольников различных типов, которые можно построить в произвольном треугольнике.
Цель исследования: разработать методику введения темы «Четырехугольники» на материале геометрии восьмого класса, осуществить подбор практических заданий для закрепления основных умений, связанных с данной темой школьного курса.
Материалы и методы исследования
Содержание данного раздела «Четырехугольники» можно условно поделить на три крупных смысловых блока: 1) введение понятия «четырехугольник», выпуклые и невыпуклые многоугольники; 2) изучение видов четырехугольников; 3) систематизация и значение темы «четырехугольники». Дадим характеристику каждому блоку.
1. Введение понятия «четырехугольник», выпуклые и невыпуклые многоугольники. Тема «Четырехугольники» по содержанию достаточно простая. Однако сложность для обучающихся представляет большое количество новых понятий, свойств и признаков различных видов четырехугольников. Для устранения путаницы между свойствами и признаками отдельных видов четырехугольников, помимо стандартной систематизации и обобщения знаний перед школьниками, необходимо раскрыть сущность понятий «свойство» и «признак», дать их структуру. Можно предложить следующие задания.
Задание 1 [4]. Что такое свойство? Назовите правила его построения.
Свойство – высказывание, которое содержит в себе необходимое условие принадлежности объекта к данному виду.
«Если объект является ______________, то___________».
Например, если четырехугольник является параллелограммом, то его диагонали пересекаются в одной точке.
Задание 2 [4]. Что такое признак? Назовите правила его построения.
Признак – утверждение, содержащее в себе достаточное условие, по которому можно отнести объект в данному виду.
«Если ___________________, то объект является_____________».
Например, если у четырехугольника диагонали пересекаются в одной точке, то этот четырехугольник параллелограмм).
Тема «четырехугольник» является традиционной для школьного курса геометрии (8 класс), однако в разных учебниках пособиях можно встретить как разную последовательность изучения элементов темы, так и трактовку самого понятия «четырехугольник». Так, в учебнике по геометрии под редакцией Л.С. Атанасяна [5] и др. и в учебнике А.В. Погорелова [6] четырехугольник вводится как каркас фигуры. Например, «четырехугольник – фигура, состоящая их четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три точки не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться» [6, с. 81].
В других учебниках (например, [7]), под четырехугольником понимается часть плоскости, ограниченная замкнутой линией их четырех звеньев, вместе с границей.
Понятие «выпуклый многоугольник» Л.С. Атанасян вводит в теме «Четырехугольник», а А.В. Погарелов в теме «Многоугольники» (9 класс). Определение четырехугольника в учебнике А.В. Погорелова уже содержит в себе условие выпуклости. Объяснение материала о выпуклых многоугольниках можно начать с задания.
Задание 3. Изобразите выпуклый и невыпуклый многоугольник (рис. 1).
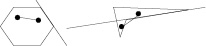
Рис. 1. Выпуклый и невыпуклый многоугольники
Обучающиеся сравнивают рисунки и подходят к характеристическому свойству:
1) выпуклый многоугольник лежит по одну сторону от любой прямой, содержащей сторону [5];
2) две любые внутренние точки многоугольника соединяются отрезком, внутри этого многоугольника [6].
После изучения понятия многоугольника, его сторон, вершин, диагоналей; внутренней и внешней областей, определения выпуклого многоугольника, ученикам можно предложить выполнить следующие задания.
Задание 5. Среди фигур, изображенных на рисунке, укажите те, которые являются:
а) многоугольниками,
б) выпуклыми многоугольниками,
в) невыпуклыми многоугольниками.
|
1
|
2
|
3
|
4
|
|
5
|
6
|
7
|
8
|
Рис. 2. Многоугольники
Начертите:
1 вариант – выпуклый пятиугольник ABCDE.
2 вариант – выпуклый шестиугольник.
Запишите в тетрадях:
а) вершины многоугольника,
б) стороны многоугольника,
в) диагонали многоугольника,
г) вычислите сумму углов многоугольника.
Чему равна сумма углов десятиугольника (работа в группах)?
Чему равна сумма углов n-угольника (работа в группах)?
Логика изложения материала данной темы в разных учебниках может быть разной. В общем случае с позиции выстраивания единой линии можно начать изучение материала с рассмотрения понятия многоугольник, далее осуществить переход к понятиям выпуклого и невыпуклого многоугольников, затем обратиться к четырехугольнику как к одному из видов многоугольников. Далее, изучаются конкретные виды четырехугольников в следующей последовательности: параллелограмм, ромб, прямоугольник, квадрат, трапеция.
2. Изучение видов четырехугольников. Изучение четырехугольников следует начать с актуализации опыта школьников (обучающиеся к этому знают прямоугольник и квадрат). Доказательства большинства теорем данного раздела проводятся с опорой на признаки равенства треугольников, которые используются при решении задач в совокупности с применением новых теоретических фактов. Учитель должен требовать, чтобы в каждом определении ученик указывал род и видовой признак, тем самым добиваясь ясного понимания соподчинения понятий.
Перед уроком, посвященным изучению темы «Параллелограмм», обучающимся можно предложить следующую задачу в качестве домашнего задания (табл. 1).
Таблица 1
Задание 6
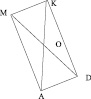
|
На рисунке отрезки АК и МD пересекаются в точке О, их общей середине. Их концы последовательно соединены отрезками. 1. Укажите равные треугольники, равные углы. Каково взаимное расположение противоположных сторон образовавшегося треугольника? 2. Какие свойства этого четырехугольника вы можете установить? |
|
|
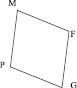
Изображены четырехугольники, противоположные стороны которых параллельны. На рис. а угол М равен 400. Определите углы этого четырехугольника. Чему равна их сумма? Какова связь противоположных углов этого четырехугольника? На рис. б и в назовите равные углы, равные треугольники, равные отрезки. Какие свойства нарисованных четырехугольников вы можете сформулировать в виде утверждений «Если_______, то________». |
а)
б)
в) |
Таблица 2
Свойства и признаки параллелограмма
|
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны |
|
|
Свойства |
Признаки |
|
1. В параллелограмме противоположные стороны равны и параллельны |
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм |
|
2. В параллелограмме противоположные стороны равны и противоположные углы равны |
2. Если в четырехугольнике противоположные стороны попарно параллельны, то четырехугольник – параллелограмм |
|
3. Диагонали параллелограмма точкой пересечения делятся пополам |
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то четырехугольник – параллелограмм |
Работая с такими заданиями, ученики в сотрудничестве с учителем получают необходимые факты, учитель подводит итоги обсуждения полученных результатов и делает обобщения. Такой подход позволяет опираться на субъектный опыт ученика при изучении геометрии.
Понятие параллелограмма вводится индуктивным путем. При отработке свойств и признаков параллелограмма необходимо дать ученикам полный их перечень. Можно предложить следующую таблицу (табл. 2).
Введение понятия «ромб» и определения ромба идет также индуктивным путем.
Сначала при изображении ромба диагонали не прорисовываются. Идет отработка понятия посредством видоизменения положения ромба. После этого ученикам дается способ построения ромба. Далее учитель дает следующее замечание: «Поскольку ромб – параллелограмм, то его свойства переходят ромбу». Можно предложить ученикам записать эти свойства самостоятельно дома. Затем изучается свойство ромба: Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Признаки выводятся и доказываются аналогично. Специально следует остановиться на признаке: «Если у четырехугольника стороны равны, то он является ромбом», так он не отмечен в учебнике как признак.
Для того чтобы подвести учеников к тому, что определение ромба в учебнике дано некорректно, ученикам предлагается задача: Дан параллелограмм, у которого две смежные стороны равны. Доказать, что это ромб». После этого возвращаются к определению, и выясняется, что достаточно потребовать равенства двух смежных сторон. При решении задач необходимо следить за четкой аргументацией со ссылками на соответствующие свойства и признаки.
Работа по изучению прямоугольника и квадрата выстраивается аналогично методике, предложенной в изучении ромба. В учебнике А.В. Погарелова [6] квадрат определяется через прямоугольник, а при помощи задачи выясняется что, квадрат – частный случай ромба. Выясняется, что к квадрату подходят все свойства ромба и прямоугольника.
В 8-м классе трапеция изучается поверхностно, так как еще не изучена тема «Подобие». Поэтому при изучении трапеции доказывается только одно свойство: сумма углов, прилежащих к одной стороне трапеции, равна 1800.
После изучения темы «Подобие» следует вернуться к теме «Трапеция» и доказать некоторые ее свойства. В сильных классах доказывается теорема: прямая, проходящая через точку пересечения диагоналей и точку пересечения боковых сторон, делит основание пополам [5].
Задачи на использование свойств и признаков различных видов четырехугольников даются в теме «Координаты и векторы». Типы таких задач:
1. Известны координаты трех вершин параллелограмма. Найти координаты четвертой вершины.
2. Доказать, что четырехугольник вершинами которого является точки с заданными координатами, является параллелограммом.
3. Систематизация и значение темы «четырехугольники». Совместно с учащимися при изучении темы следует провести классификацию четырехугольников, показав, что в зависимости от оснований классификации возможны различные определения квадрата – как ромба с прямыми углами или как прямоугольника с равными сторонами. Обязательно следует обратить внимание школьников на избыточность определений частных видов параллелограмма и уточнить эти определения. Целесообразно показать, что на основании признаков могут быть сформулированы иные определения фигур, например параллелограмма как выпуклого четырехугольника, у которого равны противоположные стороны.
Таблица 3
Обобщение и систематизация темы «Четырехугольники»
|
трапеция |
параллелограмм |
ромб |
прямоугольник |
квадрат |
|
Сумма углов прилежащих к боковым сторонам равна 1800 |
+ |
+ |
+ |
+ |
|
АО:ОС=ДО:ВО |
присутствует |
- |
+ |
+ |
|
– |
АО=СО и ВО=ДО |
+ |
+ |
+ |
|
– |
Противоположные стороны и углы попарно равны |
+ |
+ |
+ |
|
– |
отсутствует |
Диагонали взаимно перпендикулярны |
+ |
+ |
|
– |
– |
Диагонали являются биссектрисами углов |
– |
+ |
|
– |
– |
– |
Диагонали равны |
+ |
Систематизация знаний осуществляется внутри каждого пункта. В конце темы можно провести работу по обобщению и систематизации всей темы. Можно построить таблицу [4] (табл. 3).
В математических классах вводится понятие дельтоида – четырехугольника с двумя парами смежных равных сторон, получаемого их двух равнобедренных треугольников с равными основаниями путем совмещения оснований. Следует отметить, что это особый вид многоугольников, который может быть выпуклым и невыпуклым.
Результаты исследования и их обсуждение
В МОУ «Гимназия № 1» г. Соликамска была проведена экспериментальная проба по изучению темы «Четырехугольники» в аспекте рассмотренной методики. С обучающимися было проведено 14 уроков по геометрии, работа велась по учебнику геометрии под редакцией Л.С. Атанасяна [5]. В классе обучается 24 человека. За тематическую контрольную работу по теме «Четырехугольники» 7 обучающихся получили оценку «отлично», 12 обучающихся – «хорошо», 5 обучающихся – «удовлетворительно». Оценки, полученные обучающимися за контрольную работу, оказались выше, чем усредненные оценки общей успеваемости каждого обучающегося в отдельности.
Выводы
Методика, представленная в данной статье, эффективна для формирования умений, связанных с решением четырехугольников. Особое значение при обучению содержанию, связанному с четырехугольниками, нужно уделить понятиям признака и свойства, а также приемам обобщения и систематизации.
Библиографическая ссылка
Безусова Т.А. МЕТОДИКА ИЗУЧЕНИЯ ЧЕТЫРЕХУГОЛЬНИКОВ И ИХ СВОЙСТВ И ПРИЗНАКОВ // Международный журнал экспериментального образования. 2019. № 3. С. 22-26;URL: https://expeducation.ru/ru/article/view?id=11864 (дата обращения: 18.11.2025).