При проведении психолого-педагогических исследований важная роль отводится математическим методам моделирования процессов и обработки экспериментальных данных. К таким методам следует отнести, прежде всего, так называемые, вероятностно-статистические методы исследования. Это связано с тем, что на поведение как отдельного человека в процессе его деятельности, так и человека в коллективе существенное влияние оказывает множество случайных факторов. Случайность не позволяет описывать явления в рамках детерминированных моделей, т. к. проявляется, как недостаточная регулярность в массовых явлениях и, следовательно, не дает возможность с достоверностью предсказывать наступление определенных событий. Однако при изучении таких явлений обнаруживаются определенные закономерности. Нерегулярность, свойственная случайным событиям, при большом количестве испытаний, как правило, компенсируется появлением статистической закономерности, стабилизацией частот наступлений случайных событий. Следовательно, данные случайные события имеют определенную вероятность. Существуют два принципиально различающихся вероятностно-статистических метода психолого-педагогических исследований: классический и неклассический. Проведем сравнительный анализ этих методов.
Классический вероятностно-статистический метод. В основе классического вероятностно-статистического метода исследования лежат теория вероятностей и математическая статистика. Данный метод применяется при изучении массовых явлений случайного характера, он включает несколько этапов, основные из которых следующие.
1. Построение вероятностной модели реальности, исходя из анализа статистических данных (определение закона распределения случайной величины). Естественно, что закономерности массовых случайных явлений выражаются тем более отчетливо, чем больше объем статистического материала. Выборочные данные, полученные при проведении эксперимента, всегда ограничены и носят, строго говоря, случайный характер. В связи с этим важная роль отводится обобщению закономерностей, полученных на выборке, и распространению их на всю генеральную совокупность объектов. С целью решения этой задачи принимается определенная гипотеза о характере статистической закономерности, которая проявляется в исследуемом явлении, например, гипотеза о том, что исследуемое явление подчиняется закону нормального распределения. Такая гипотеза носит название нулевой гипотезы, которая может оказаться ошибочной, поэтому наряду с нулевой гипотезой еще выдвигается и альтернативная или конкурирующая гипотеза. Проверка того насколько полученные экспериментальные данные соответствуют той или иной статистической гипотезе осуществляется с помощью так называемых непараметрических статистических критериев или критериев согласия. В настоящее время широко используются критерии согласия Колмогорова, Смирнова, омега-квадрат и др. [3]. Основная идея этих критериев состоит в измерении расстояния между функцией эмпирического распределения и функцией полностью известного теоретического распределения. Методология проверки статистической гипотезы строго разработана и изложена в большом количестве работ по математической статистике.
2. Проведение необходимых расчетов математическими средствами в рамках вероятностной модели. В соответствии с установленной вероятностной моделью явления проводятся вычисления характеристических параметров, например, таких как математическое ожидание или среднее значение, дисперсия, стандартное отклонение, мода, медиана, показатель асимметрии и др.
3. Интерпретация вероятностно-статистических выводов применительно к реальной ситуации.
В настоящее время классический вероятностно-статистический метод хорошо разработан и широко используется при проведении исследований в различных областях естественных, технических и общественных наук. Подробное описание сути данного метода и его применения к решению конкретных задач можно найти в большом количестве литературных источников, например в [1, 3].
Неклассический вероятностно-статистический метод. Неклассический вероятно-статистический метод исследований отличается от классического тем, что он применяется не только к массовым, но и к отдельным событиям, имеющим принципиально случайный характер. Данный метод может быть эффективно использован при анализе поведения индивида в процессе выполнения той или иной деятельности, например, в процессе усвоения знаний учащимся [4]. Особенности неклассического вероятностно-статистического метода психолого-педагогических исследований рассмотрим на примере поведения учащихся в процессе усвоения знаний.
Впервые вероятностно-статистическая модель поведения учащихся в процессе усвоения знаний была предложена в работе [5]. Дальнейшее развитие этой модели было сделано в работе [6]. Учение как вид деятельности, цель которого приобретение человеком знаний, умений и навыков, зависит от уровня развития сознания учащегося. В структуру сознания входят такие познавательные процессы, как ощущение, восприятие, память, мышление, воображение. Анализ этих процессов [6, 9] показывает, что им присущи элементы случайности, обусловленные случайным характером психического и соматического состояний индивида, а также физиологическим, психологическим и информационным шумами при работе головного мозга. Последнее привело при описании процессов мышления к отказу от использования модели детерминистской динамической системы в пользу модели случайной динамической системы [10]. Это означает, что детерминизм сознания реализуется через случайность. Отсюда можно заключить, что знания человека, являющиеся фактически продуктом сознания, также имеют случайный характер, и, следовательно, для описания поведения каждого отдельного учащегося в процессе усвоения знаний может быть использован вероятностно-статистический метод.
В соответствии с этим методом учащийся идентифицируется функцией распределения (плотностью вероятности), определяющей вероятность нахождения его в единичной области информационного пространства. В процессе обучения функция распределения, с которой идентифицируется учащийся, эволюционируя, движется в информационном пространстве. Каждый учащийся обладает индивидуальными свойствами и допускается независимая локализация (пространственная и кинематическая) индивидов друг относительно друга.
На основе закона сохранения вероятности записывается система дифференциальных уравнений, представляющих собой уравнения непрерывности, которые связывают изменение плотности вероятности за единицу времени в фазовом пространстве (пространстве координат, скоростей и ускорений различных порядков) с дивергенцией потока плотности вероятности в рассматриваемом фазовом пространстве. В [4] проведен анализ аналитических решений ряда уравнений непрерывности (функций распределения), характеризующих поведение отдельных учащихся в процессе обучения.
При проведении экспериментальных исследований поведения учащихся в процессе усвоения знаний используется вероятностно-статистическое шкалирование [7], в соответствии с которым шкала измерений представляет собой упорядоченную систему <A; Ly, F, G; f, M>, где A – некоторое вполне упорядоченное множество объектов (индивидов), обладающих интересующими нас признаками (эмпирическая система с отношениями); Ly – функциональное пространство (пространство функций распределения) с отношениями; F – операция гомоморфного отображения A в подсистему Ly; G – группа допустимых преобразований; f – операция отображения функций распределения из подсистемы Ly на числовые системы с отношениями n-мерного пространства M. Вероятностно-статистическое шкалирование применяется для нахождения и обработки экспериментальных функций распределения и включает три этапа.
1. Нахождение экспериментальных функций распределения по результатам контрольного мероприятия, например, экзамена. Типичный вид индивидуальных функций распределения, найденных при использовании двадцатибалльной шкалы, представлен на рис. 1. Методика нахождения таких функций описана в [7].
2. Отображение функций распределения на числовое пространство. С этой целью проводится расчет моментов индивидуальных функций распределения. На практике, как правило, достаточно ограничиться определением моментов первого порядка (математического ожидания), второго порядка (дисперсии) и третьего порядка, характеризующего асимметрию функции распределения.
3. Ранжирование учащихся по уровню знаний на основе сравнения моментов различных порядков их индивидуальных функций распределения.
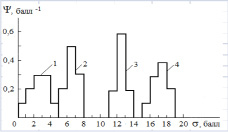
Рис. 1. Типичный вид индивидуальных функций распределения студентов, получивших на экзамене по общей физике различные оценки [7]: 1 – традиционная оценка «2»; 2 – традиционная оценка «3»; 3 – традиционная оценка «4»; 4 – традиционная оценка «5»
На основе аддитивности индивидуальных функций распределения в [8] найдены экспериментальные функции распределения для потока студентов (рис. 2).
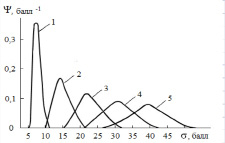
Рис. 2. Эволюция полной функции распределения потока студентов, аппроксимированной гладкими линиями [8]: 1 – после первого курса; 2 – после второго курса; 3 – после третьего курса; 4 – после четвертого курса; 5 – после пятого курса
Анализ данных, представленных на рис. 2, показывает, что по мере продвижения в информационном пространстве функции распределения расплываются. Это происходит вследствие того, что математические ожидания функций распределения индивидов движутся с разными скоростями, а сами функции расплываются из-за дисперсии. Дальнейший анализ данных функций распределения может быть проведен в рамках классического вероятностно-статистического метода.
Обсуждение результатов. Анализ классического и неклассического вероятностно-статистических методов психолого-педагогических исследований показал, что между ними имеется существенное отличие. Оно, как это можно понять из сказанного выше, заключается в том, что классический метод применим лишь к анализу массовых событий, а неклассический метод применим как к анализу массовых, так и одиночных событий. В связи с этим классический метод может быть условно назван массовым вероятностно-статистическим методом (МВСМ), а неклассический метод – индивидуальным вероятностно-статистическим методом (ИВСМ). В 4] показано, что ни один из классических методов оценки знаний учащихся в рамках вероятностно-статистической модели индивида не может быть применен для этих целей.
Отличительные особенности методов МВСМ и ИВСМ рассмотрим на примере измерения полноты знаний учащихся. С этой целью проведем мысленный эксперимент. Предположим, что имеется большое количество абсолютно одинаковых по психическим и физическим характеристикам учащихся, имеющих одинаковую предысторию, и пусть они, не взаимодействуя друг с другом, одновременно участвуют в одном и том же познавательном процессе, испытывая абсолютно одинаковое строго детерминированное воздействие. Тогда в соответствии с классическими представлениями об объектах измерения все учащиеся должны были бы получить одинаковые оценки полноты знаний с любой заданной точностью измерений. Однако в реальности при достаточно большой точности измерений оценки полноты знаний учащихся будут различаться [7]. Объяснить такой результат измерений в рамках МВСМ не представляется возможным, т. к. исходно предполагается, что воздействие на абсолютно одинаковых невзаимодействующих между собой учащихся имеет строго детерминированный характер. Классический вероятностно-статистический метод не учитывает того, что детерминизм процесса познания реализуется через случайность, внутренне присущую каждому познающему окружающий мир индивиду.
Случайный характер поведения учащегося в процессе усвоения знаний учитывает ИВСМ. Применение индивидуального вероятностно-статистического метода для анализа поведения рассматриваемого идеализированного коллектива учащихся показало бы, что указать точно положение каждого учащегося в информационном пространстве нельзя, можно лишь говорить вероятности нахождения его в той или иной области информационного пространства. Фактически каждый учащийся идентифицируется индивидуальной функцией распределения, причем ее параметры, такие как математическое ожидание, дисперсия и др., индивидуальны для каждого учащегося. Это означает, что индивидуальные функции распределения будут находиться в разных областях информационного пространства. Причина такого поведения учащихся заключается в случайном характере процесса познания.
Однако в ряде случаев результаты исследований, добытые в рамках МВСМ, могут быть интерпретированы и в рамках ИВСМ. Предположим, что преподаватель при оценке знаний учащегося использует пятибалльную шкалу измерений. В этом случае погрешность в оценке знаний составляет ±0,5 балла. Следовательно, когда учащемуся выставляется оценка, например, 4 балла, это означает, что его знания находятся в промежутке от 3,5 баллов до 4,5 баллов. Фактически положение индивида в информационном пространстве в данном случае определяется прямоугольной функцией распределения, ширина которой равна погрешности измерения ±0,5 балла, а оценка является математическим ожиданием. Эта погрешность настолько большая, что не позволяет наблюдать истинный вид функции распределения. Однако, несмотря на столь грубую аппроксимацию функции распределения, изучение ее эволюции позволяет получить важную информацию, как о поведении отдельного индивида, так и коллектива учащихся в целом [4].
На результат измерения полноты знаний учащегося непосредственно или опосредовано влияет сознание преподавателя (измерителя), которому также свойственна случайность. В процессе педагогических измерений фактически имеет место взаимодействие двух случайных динамических систем, идентифицирующих поведение учащегося и преподавателя в данном процессе. В [8] рассмотрено взаимодействие студенческой подсистемы с профессорско-преподавательской подсистемой и показано, что скорость движения математического ожидания индивидуальных функций распределения студентов в информационном пространстве пропорциональна функции воздействия профессорско-преподавательского коллектива и обратно пропорциональна функции инертности, характеризующей неподатливость изменению положения математического ожидания в пространстве (аналог закона Аристотеля в механике).
В настоящее время, несмотря на значительные достижения в разработке теоретических и практических основ измерений при проведении психолого-педагогических исследований, проблема измерений в целом еще далека от решения. Это связано, прежде всего, с тем, что до сих пор не имеется достаточной информации о влиянии сознания на процесс измерения. Аналогичная ситуация сложилась и при решении проблемы измерений в квантовой механике. Так, в работе [2] при рассмотрении концептуальных проблем квантовой теории измерений говорится о том, что разрешить некоторые парадоксы измерений в квантовой механике «… вряд ли возможно без непосредственного включения сознания наблюдателя в теоретическое описание квантового измерения». Далее говорится, что «… непротиворечивым является предположение о том, что сознание может сделать вероятным некоторое событие, даже если по законам физики (квантовой механики) вероятность этого события мала. Сделаем важное уточнение формулировки: сознание данного наблюдателя может сделать вероятным, что он увидит это событие».
Выводы
1. Неклассический (индивидуальный) вероятностно-статистический метод психолого-педагогических исследований в отличие от классического (массового) вероятностно-статистического метода применим не только для анализа поведения больших коллективов учащихся в процессе усвоения ими знаний, но и каждого отдельно взятого учащегося.
2. ИВСМ учитывает вероятностно-статистический характер поведения учащихся в процессе обучения и позволяет тонко ранжировать их по полноте знаний.
3. Успехи на пути решения проблемы измерений при проведении психолого-педагогических исследований будут во многом зависеть от достижений в понимании сути сознания человека и его влияния на процесс измерений.
Библиографическая ссылка
Романов В.П., Соколова Н.А. СРАВНИТЕЛЬНЫЙ АНАЛИЗ КЛАССИЧЕСКОГО И НЕКЛАССИЧЕСКОГО ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКИХ МЕТОДОВ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ИССЛЕДОВАНИЙ // Международный журнал экспериментального образования. 2013. № 10-1. С. 42-46;URL: https://expeducation.ru/ru/article/view?id=4118 (дата обращения: 15.02.2026).

