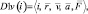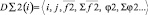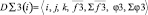Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Voronova L.I. 1, 2 Trunov A.S. 1 Voronov V.I. 1, 2

---

1 Russian State University for the Humanities

2 National Research University Higher School of Economics

Статья в формате PDF

990 KB

1. Brown W.M., Kohlmeyer A., Plimpton S.J., Tharrington A.N. Implementing molecular dynamics on hybrid high performance computers – Particle-particle particle-mesh // Computer Physics Communications. – Vol. 183(3). – 2012. – P. 449–459.

2. Harvey M.J., De Fabritiis G. An implementation of the smooth particle mesh Ewald method on GPU hardware // Journal of Chemical Theory and Computation. – Vol. 5 (9). – 2009. – P. 2371–2377.

3. Jha P.K., Sknepnek, R., Guerrero-García, G.I., Olvera De La Cruz, M. A graphics processing unit implementation of coulomb interaction in molecular dynamics // Journal of Chemical Theory and Computation. – Vol. 6(10). – 2010. – P. 3058–3065.

4. Le Grand S., Götz A.W., Walker R.C. SPFP: Speed without compromise – A mixed precision model for GPU accelerated molecular dynamics simulations // Computer Physics Communications. – Vol. 184(2). – 2013. – P. 374–380.

5. Peter, E., Pande, V.S. Efficient nonbonded interactions for molecular dynamics on a graphics processing unit // Journal of Computational Chemistry Vol. 31(6). – 2010. – P. 1268–1272.

6. Research-Information System (RIS) «MD-SLAG-MELT»: http://www.nano-md-simulation.com.

7. Voronova L.I., Grigorieva M.A. Information model of physical-chemical melt properties developing for the research complex MD_SLAGMELT”// Interbranch information service. – 2011. – № 2. – Р. 30–36.

8. Voronova L.I., Grigorieva M.A., Voronov V.I. Nanostruсture computer modeling methods development for multicomponent slag melts // Fundamental researches. – 2011. – № 8 (part 3). – Р. 617–622. http://www.rae.ru/fs/?section = content&op = show_article&article_id = 7981162.

9. Voronova L.I.,.Grigorjeva M.A., Voronov V.I., Trunov A.S. Computer simulation of the polymerizable oxide melts nanostructure using the descriptor-graph model // Materials Science and Metallurgy Engineering. – 2013. – № 1. – P. 1–12. DOI:10.12691/msme-1-1-1 http://pubs.sciepub.com/msme/1/1/1/#12.

10. Voronova L.I., Grigorjeva M.A., Voronov V.I., Trunov A.S. The program complex «MD-SLAG-MELT» modeling nanostructure and properties of multicomponent melts // Melts. – 2013. – № 2. – Р. 1–14.

11. Voronova L.I., Trunov A.S. The parallel algorithm optimization for distributed molecular-dynamic modeling system // Interindustry information service (IIS). – 2011. – № 3. – Р. 1–12. http://infogoz.vimi.ru/Izdanie/MIC_03_11.htm#chaper1.

12. Voronova L.I., Trunov A.S. Subsystem of distributed molecular dynamics simulation information research system «MD-SLAG-MELT». – Certificate of state registration of computer program № 2012615017, 5.06.2012.

The model of distributed calculators makes it possible a parallel calculation of the correlated N-particle system with a complex multi-particle interaction (long-range ionic and short-range repulsive, two- and three-particle covalent interactions) with MPI and CUDA technologies. The computational model is based on the mathematical model of heterogeneous descriptors developed by the authors, that allows shift the focus from the describing the physical interactions in the system to the description of data flow between the descriptors. The results of computer experiments, which compare the time of the simulation on the cluster of 16 calculators and GPU NVIDIA are given. The model of distributed calculators was being tested with the software package of RIS «MD-SLAG-MELT»[1].

Nowadays, computer modeling (CM) is widely used in various fields of modern science. In particular, in physical chemistry we can study the properties and structure of materials and their relationships.

Molecular-dynamic (MD), Monte-Carlo and quantum-chemical methods are applied there and allow to define different sets of properties. The molecular-dynamics method allows to define the whole complex of properties (structural, thermodynamic, transport) and to investigate the interrelations of nanostructure and physical-chemical properties [1–5].

The size of the simulated system for MD modeling is extremely important. A significant increase in the size of the system provides the practical relevance of the results. The calculation of the systems with 105–107 particles requires a large amount of time and computer resources and it makes impossible carrying out CM without high-performance computing [6, 7]. To solve this problem, the authors have developed a model of distributed calculators based on distributed computing methods for correlated N-particle system [8–10].

Physical phenomena that are adequately described by the classical and quasiclassical theory can be simulated (using models of particles) by molecular dynamics method. The term «model of particles» is the general one for a class of computing models in which the discrete description of the physical phenomena includes cooperating particles. Each modeling particle has a set of constant and variable attributes.

In this case molecular-dynamic simulation represents the numerical solution of the Cauchy’s boundary task, which means that the initial system state in a bounded region of space (calculation area) is specified at the time t = 0 and the boundary conditions are reserved on it. Modeling is tracking the time evolution of this configuration. The main part of calculation is the cycle on a time step in which the state of physical system changes on time for a small step Δt.

The current condition of the physical system is defined by the attributes of the final ensemble of particles, and the evolution of the system is defined by the interaction laws of these particles. The most of the molecular-dynamics systems relates to the class of long-range potentials, or considering only short-range covalent interactions.

The subject of this work is an investigation of the polymerizing systems with multi-particle interactions which means uniting some types of interactions – two-particle contribution (long-range ionic and short-range repulsive) and multi-particle ones (two and three-particle covalent interactions). The description of this class of models is given in Table 1 [10].

The ionic model is a part of ionic-covalent model though for modeling ionic connections it can be used only independently. In the ionic model (IM) potential functions are built for the ion system. The IM includes models of short-range repulsive and long-range Coulomb interaction. The last one is calculated by the Ewald method or the fast multipole method.

The ionic-covalent model is more realistic to describe the interactions in the polymerizing systems. The model is based on the polymer theory of the slags, which suggests the presence of small non-destructive structural groups (elementary structure groups – ESG), which form the structural grid in the polymerizing melts.

Table 1

The interparticle interaction models are used in the information research system «MD-Slag-Melt» [10]

The ICM unites the ionic model, the models of two- and three-particle covalent interaction in the elementary structure groups, the three-particle covalent interaction for bridge bonds, the environmental effects for the network forming atoms-oxygen bounds inside the ESG from the nearest neighbors outside ESG.

The features of the above mentioned physicochemical models require the development of a mathematical model that allows realizing high-performance computing for correlated systems with complex interactions containing 105–107 particles.

For solution the authors have developed a model of heterogeneous descriptors for distributed MD simulation of the correlated system of N-particles.

The basic elements of the model are the object and the descriptor, which provide the possibility of calculations distribution without detail specification of all interactions between the particles

We define an object as a set of particles descriptions and relations between them for the system in the initial state, which is built by specific rules and provides the possibility of the system decomposition for distributing and parallel calculations.

The objects are initialized by means of heterogeneous descriptors which contain polytypic elements of the description of the allocated object which is necessary for the distribution of calculations.

Thus, the system is a set of the objects characterized by heterogeneous descriptors the calculation of which can be distributed on separate calculators, combining results on a certain scheme.

On the basis of physicochemical models and the analysis of the program code of a local MD application, the authors have constructed a set of descriptors allowing to share the application code into independent blocks between calculators. The descriptors can be divided into two classes: one-particle descriptors and aggregators (two – and three-particle descriptors).

Both classes of descriptors include the possibility of parallel computing on different calculators. However, if the one-particle descriptors can be distributed on the calculators independently, then the aggregators (containing the elements describing the cross relations of different orders between one-particle descriptors and/or aggregators) are «dependant» on the one-particle descriptor. The aggregators are computed on the same computer with a «parental» one-particle descriptor.

The notation of local molecular-dynamic model in model of descriptors for distribution MD simulating is given in Table 2.

Thus, the set of objects and their relationship between them are devided into different types of subset according to heterogeneous descriptor.

More detailed characteristic of descriptors elements are given below.

{D1(i)} – the class of one-particle descriptors assuming distribution. It is expedient to divide this descriptor into two subset.

{D1s(i)} – a subset of the descriptors, containing constant scalar attributes of particles. Here D1s(i) = <I, σ q, m, tip,>, where i – particle number, tip – particle type, m – weight, q – charge, σ – rigid sphere radius.

{D1v(i)} – a subset of the descriptors containing variable vector attributes of particles. Here

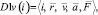
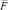where – radius vector; – speed; – acceleration; – full force effecting on an i-particle at a given timestep.

{D∑(i)} – the class of heterogeneous descriptors providing creation of different orders relations between descriptors of different types. Some elements of the descriptors in the class are the storage, so these descriptors are called aggregators.

Three types of subset aggregators are defined by the authors.

1. {D∑2(i)} – a subset of the two-particle aggregators containing scalar and vector elements. They provide the calculation of cross relations, on the basis of one-particle descriptors, and also contain scalar and vector stores. The aggregators depend on one-particle descriptors (called «brunches»). Data for calculation are received from «parental» descriptor. The aggregator realizes consequent calculation of all pair relations between fixed i- object and others to form storages.

Table 2

Distributed descriptor model of molecular-dynamic modeling N-particle correlation system

Here

,

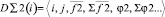where i, j – particles numbers; 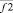– force acting between i and j particles; φ2 – two-particle potential; 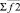– the vector storage including different types of contributions to two-particle force effecting on an i-particle; Σφ2 – the scalar storage containing values of different power contributions to total two-particle energy.

2. {D∑3(i)} – a subset of three-particle aggregators which build third order cross relations on the basis of one-particle descriptors. Each aggregator contains the variable vector and scalar elements which are calculated on special algorithms, providing formation of limited selections of particles (elementary groups) from all range of numbers. The aggregators calculate the relations between triplets of particles within these selections. Like two-particle aggregators it contains scalar and vector stores being brunches in relation to a pair of one-partial descriptors.

Here

,

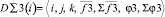where i, j, k – triplets of particles from elementary groups; 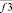– three-particle interaction; φ3 – three- particle potential; 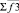– the vector storage including different types of contributions to the three- particle force acting on an i-particle; Σφ3 – the scalar storage containing values of different power contributions to total three- particle energy.

3. {D(Property)} – aggregators subset containing elements, describing macroscopic properties of the system, based on two- particle and three- particle aggregators. Here

D (Property) = <T, P, E, C, γV, αP, ,bT, χa, msda, h, x, l>,

where a – type of particles; T – temperature; P – pressure; the С – heat capacity; E – energy; γV – coefficient of thermal pressure; αP – coefficient of thermal expansion, bT – isothermal compressibility; χa – velocity autocorrelation function; msda – mean square displacement; Da – diffusion coefficient; h, x, l – viscosity factor, coefficient of conductivity and thermal conductivity. These aggregators cannot be distributed.

The method of heterogeneous descriptors make it possible to transfer the accent from physical interactional in the system to information description of data flows redistribution between descriptors and use this approach to form computing model of redistributed calculation on the bases of heterogeneous descriptors.

The model of distributed calculators is based on a master-slave methodology. The master controls the slaves, separates a set of particles into subsets which are transferred to the slaves for calculation. The master receives data from the slaves and processes the results. The slaves calculate the N-particle system on the CPU or the GPU, using MPI and CUDA technologies.

The model of distributed calculators is given in Fig. 1.

The model assumes the implementation of distributed computing a heterogeneous computing environment. The calculators have different performance and type, such as the GPU and CPU [11].

On the first step of modeling the all set of particles is transmitted to every calculator. The master generates a subset of particles that will be transferred to the calculators for processing. At run time of work, each slave receives data from the master about the calculated subset of the particle. The slave provides interactions calculation describing descriptors D∑2(i) и D∑3(i), associated with the i particle, according to a given scheme. When each slave completes the calculation, it passes the results to master which gathers and processes data.

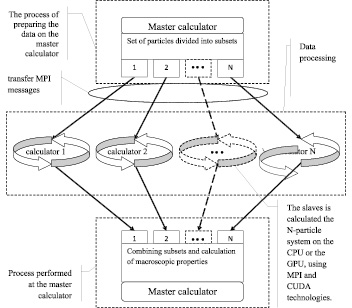
Fig. 1. The model of distributed calculators using the CUDA and MPI technologies

The most pressing is to ensure parallel calculation of objects characterized by the descriptors D∑2(i), since the implementation of this part simulation has the largest computating time (a quadratic dependence on the number of particles N2). Flowchart of the calculators work based on the model of heterogeneous descriptors is given in Fig. 2.

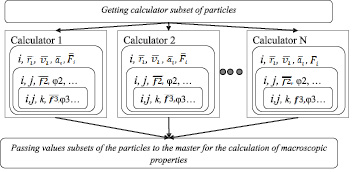
Fig. 2. Flowchart of the calculators work based on the model of heterogeneous descriptors

The formal description of parallel calculation correlated N-particle system using CUDA and MPI, is given in Fig. 3 and 4 in the form of pseudo-code.

To make parallel calculation of correlated N-particle system using the technology MPI calculators are placed in communication field of MPI_COMM_WORLD. Each calculator is given a unique number, stored in the variable rank. Data on the calculators quantity are stored in a variable size.

MPI_BCAST function (a variable containing the information of the quantity of descriptors in a subset, quantity of values containing in the variable, variable type, transmitter, communication area, error number) sends to each calculator the number of descriptors for further combining. The calculators independently determine their own subset of the descriptors, using variables StrSml and FshSml. The variables correspond to the start and final value of the subset descriptors and set computing field for calculator.

Fig. 3. Pseudocode parallel calculation of correlated N-particle system with MPI technology

After completion of computing calculators call the function MPI_GATHER (new values of elements of a subset descriptors {Dlv(i)}, number of values, data type, variable for the gather subsets of descriptors on the master, variable contains number of descriptor elements, variable type, communication area, error number) that sends a subset of the one-particle descriptors {Dlv(i)}to the master for their combining.

The calculation of the correlated N-particle system at CUDA is divided into two parts. In sequential part there are set of variables(memory GPU). In the GPU memory values of the elements of one-particle descriptors are placed. The subsets of descriptors distributed between processor threads and when the parallel calculation is completed the new values of the elements {Dlv(i)} are combined in RAM on the master.

Descriptions are distributed between threads in parallel part. Then each thread conducts its independent calculation and stores the data in memory GPU.

To estimate the efficiency of the distributed calculators model a number of experiments are carried out. The spared time for modeling using MPI and CUDA technologies are compared. Descriptors are filled with test values of the elements. For the model using MPI technology organized cluster containing 16 calculators. Testing of the model using CUDA technology was carried out on the processor GForce GTS 450. The results of computer simulations to model distributed calculators are given in Table 3.

According to the results of the simulation the least time is observed at the calculation of the system GPU GTS 450. At the calculation using MPI technology it is not possible to achieve the acceleration equal to the number of processors because frequent calls to slow speed RAM. In the code on the GPU provides accommodation of variables in a quick shared and constant memory, which reduces the simulation time.

The model of heterogeneous descriptors allows to create a computing model, which is used MPI and CUDA technology for GPU and CPU and allows to obtain experimental results of practical value.

Fig. 4. Pseudocode parallel calculation of correlated N-particle system with CUDA technology

Table 3

The results of computer simulations to model distributed calculators

The model of distributed calculators was being tested win the software package of RIS «MD-SLAG-MELT» [1], [12].

The study was supported by The Ministry of education and science of Russian Federation, project 14.132.21.1792.

The work was submitted to the International Scientific Conference «Modern high technologies» Spain-France, July 27 - on August 3, 2013, came to the editorial office оn 24.07.2013.

Библиографическая ссылка