Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Айдосов А.А. 1 Айдосов Г.А. 1 Нарбаева С.М. 1

---

1 «Научно-исследовательский институт математики и механики» РГП на ПХВ «Казахский национальный университет им. аль-Фараби» Министерства образования и науки Республики Казахстан

Статья в формате PDF

3335 KB

1. Айдосов А.А., Айдосов Г.А. Теоретические основы прогнозирования природных процессов и экологической обстановки окружающей среды. Книга 1, Теоретические основы прогнозирования атмосферных процессов и экологической обстановки окружающей среды. – Алматы: Изд-во «Қазақ университеті», 2000. – 290 с.

2. Айдосов А.А., Айдосов Г.А., Заурбеков Н.С. Моделирование распространения вредных веществ в нижнем слое атмосферы со свободной верхней границей воздушной массы и оценка экологической обстановки окружающей среды.// Промышленность Казахстана. – Алматы. – 2007. – № 1(40). – С. 68–70.

3. Нигматулин Р.И. Методы механики сплошной среды для описания многофазных смесей // ПММ. – 1970. – Т. 34, № 6. – С. 1097–1112.

4. Айдосов А.А., Дюсенова Ж.А., Айдосов Г.А., Кожаметов С.Н. Исследование состояния воздушного бассейна с учетом взаимодействия природно-климатических условий и техногенных факторов // Труды 7-ой Международной научно-практической конференции. – Алматы, том II. – 2005. – С. 283–289.

5. Бакирбаев Б., Керимкул Ж. Численная модель турбулентной диффузии примесей в пограничном слое атмосферы // Природопользование и проблемы антропосферы: Вестн. ТарГУ им. М.Х.Дулати. – Тараз, 2001. – № 4. – С. 123–130.

6. Палюх Б.В., Ветров А.Н. Использование методов математического моделирования в системе мониторинга безопасности городского хозяйства // Научная конференция, посвященная 70-летию со дня рождения академика В.А. Мельникова. – М.: Научный Фонд «Первая Исследовательская Лаборатория имени академика В.А. Мельникова», 1999. – С. 203–204.

7. Perminov V. Mathematical modeling of crown forest fire initiation // Lecture Notes in Computer Science, Vol. 2667, 2003. – P. 549–557.

8. Берлянд М.Е. К теории турбулентной диффузии. – Тр. ГГО, вып.138, С.31-37. 1963 г.

9. Я.Б.Попов. Статистические методы анализа и контроля качества и надежности. – М.: Светское радио, 1962.

10. Банин А.П. Эффективность мероприятий по оценке природных ресурсов. – М.: Стройиздат, 1979. – 88 с.

11. Miyakoda K., Rosati A. One-way nested grid models: The interface condition and the numerical accuracy // Mon. Weather Review. –1977. – Vol. 105. – P. 1092–1107.

12. Гришин А.М. Математические модели лесных пожаров и новые способы борьбы с ними. Новосибирск: Наука, 1992.

Газообразные и конденсированные продукты выбрасываются в окружающую среду в результате работы промышленных предприятий и автотранспорта, например, оксиды углерода, азота и серы, альдегиды, бензапирен, свинец и др. В приземном слое в процессе фотохимических реакций образуются озон и другие, опасные для здоровья человека и состояния растительного и животного мира токсиканты. При определенных метеорологических условиях даже незначительные выбросы загрязняющих веществ могут создавать неблагополучную экологическую обстановку в населенных пунктах. Еще большую опасность представляет природные и техногенные катастрофы, в результате которых возможно крупномасштабное загрязнение природной среды. Возникновение пожаров на значительных территориях, в том числе лесных, может привести к таким явлениям, как огненный шторм и «ядерная зима». Кроме того, в последнее время становятся актуальными проблемы, связанные с защитой водной среды от загрязнения.

А экспериментальное, промышленные и полупромышленные, а так же натурные изучение вышеуказанных явлений условиями является очень дорогостоящим, а в отдельных случаях не представляется возможным проводить полное физическое моделирование, представляют интерес теоретические методы исследования – методы математического моделирования. В этом случае объект изучения не само явление, а его математическая модель, которая может представлять собой систему дифференциальных уравнений в частных производных с соответствующими начальными и граничными условиями.

В рамках данной проблемы один из наиболее сложных и наименее разработанных (в том числе и в методическом плане) вопросов связан с исследованиями по изучению изменений компонентов природной среды, методами математического моделирования в условиях различного рода техногенных загрязнений. Эти исследования являются одним из важных этапов экологической программы, они вскрывают особенности воздействия антропогенной нагрузки на среду обитания.

В данной работе рассматривается математическое моделирование, использующее детерминированный подход, со следующими этапами/1-12/:

1. Физический анализ изучаемого явления и создание физической модели объекта.

2. Определение реакционных свойств среды, коэффициентов переноса и структурных параметров среды и вывод основной системы уравнений с соответствующими начальными и граничными условиями.

3. Выбор метода численного или аналитического метода решения поставленной краевой задачи.

4. Получение дискретного аналога для соответствующей системы уравнений, если предполагается численное решение.

5. Выбор метода получения решения для дискретного аналога.

6. Разработка программы расчета для вычислительной машины. Тестовые проверки программы расчета. Получение численного решения системы дифференциальных уравнений.

7. Сравнение полученных результатов с известными экспериментальными данными, их физическая интерпретация. Параметрическое изучение исследуемого объекта.

Главное требование к математической модели – согласованность полученных результатов численного анализа с данными натурного наблюдения и экспериментальных исследований. Для выполнения этого достаточного условия необходимо, чтобы:

• в математической модели выполнялись фундаментальные законы сохранения массы, энергии и импульса;
• математическая модель правильно отражала сущность изучаемого явления.

Для исследования вышеупомянутых сложных явлений перспективно использование понятий и методов механики сплошных многофазных многокомпонентных многоскорост-ных реагирующих сред.

Таким образом, с помощью построенной математической модели (в приземном слое атмосферы, в водной среде и т.д) можно исследовать динамику распространения загрязнения под влиянием различных внешних условий (температуры воздуха, скорости ветра, температурной стратификации в атмосфере и т.д.), а также параметров источника загрязнения. Сравнивая полученные данные с установленными предельно – допустимыми концентрациями (ПДК), можно проанализировать уровни загрязнения по различным компонентам в различные моменты времени и предложить пути снижения концентрации загрязнений воздушного бассейна. Процесс переноса моделируется смешанной краевой задачей математической физики и включает уравнение переноса с учетом турбулентной диффузии. При постановке задачи граничные условия задаются на самом нижнем слое z = 0 и на самом верхнем слое z = h3, рассматриваются условия сопряжения на границах разделения слоев.

Моделирование региональных атмосферных процессов реализуется с учетом того, что поля метеорологических величин в ограниченной области формируются под влиянием макромасштабных циркуляций атмосферы. Поэтому ограниченная область решения рассматривается как часть некоторого целого, и нестационарные краевые условия на ее боковых границах формулируются на основе данных, полученных для окаймляющей области. Кроме этого, при численном решении задач прогноза состояния атмосферы для ограниченной территории появляется необходимость сгущать сетку для достижения требуемой точности решения задачи в местах больших градиентов зависимых функций.

Слой почвы можно разделить на три части: поверхность почвы, являющейся границей двух сред; слой суточных колебаний температуры (~1 м); слой годовых колебаний температуры (~10 м). Толщина выделенных в почве слоев зависит от свойств почвы.

Неизвестных функций в уравнениях гидродинамики турбулентной атмосферы и диффузии примесей представим в виде суммы: Y(t, x, y, z) = 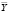(t) + Y′(t, x, y, z), где 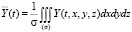– среднее значение функции в блоке (σ – объем блока), а Y′(t, x, y, z) – отклонение от среднего внутри блока. И затем усредним уравнения гидродинамики турбулентной атмосферы и диффузии примесей по объему блока σ, используя свойства операции осреднения: 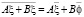, , 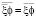, , 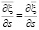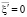где: x, j – функции независимых переменных x, y, z, t; A, B – постоянные; s – любая из этих независимых переменных.

Записав уравнения гидродинамики турбулентной атмосферы и диффузии примесей используя методов механики сплошных многофазных многокомпонентных многоскорост-ных реагирующих сред для каждого блока модели с учетом взаимодействия между блоками и присоединив к ним уравнения переноса веществ и радиации, получим систему уравнений блочной модели локального процесса:

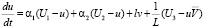, (i = 1, 2, 3);

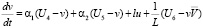, (i = 1, 2, 3);

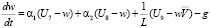, (i = 1, 2, 3); (1)

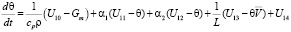, (i = 1, 2, 3);

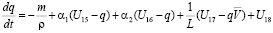, (i = 1, 2, 3);

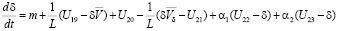, (i = 1, 2, 3);

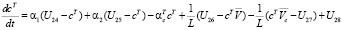, (i = 1, 2, 3);

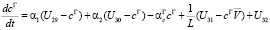, (i = 1, 2, 3);

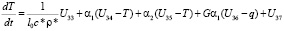, (i = 0);

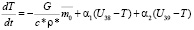, (i = -1, -2);

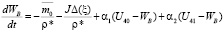, (i = -1, -2);

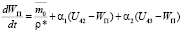, (i = -1, -2);

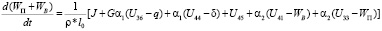, (i = 0).

Скорость фазовых переходов влаги m в случае термодинамического процесса в воздухе, насыщенном водяным паром, определяется формулой:

,

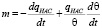где

, ;

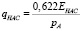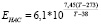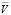 – скорость ветра; , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

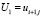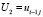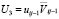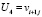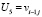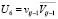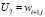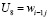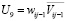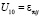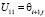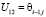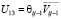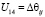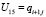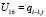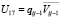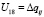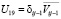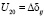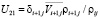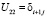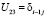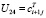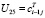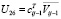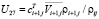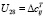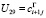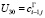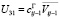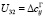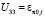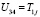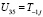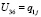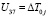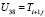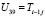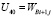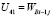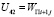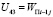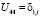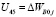где: 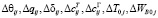– антропогенные добавки в слои модели; i – номер блока по вертикали; j – номер блока по горизонтали; i-1 – номер соседнего блока снизу; i+1 – номер соседнего блока сверху; j-1 – номер блока, из которого дует ветер; j+1 – номер следующего блока по воздушному потоку, , .

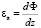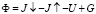Следовательно, в предлагаемой блочной модели локального процесса довольно просто с математической точки зрения записана основная система уравнений, но вследствие схематизации процессов появились дополнительные коэффициенты, при поиске которых максимально используются известные физические закономерности и выражающие теоретические, полуэмпирические и эмпирические формулы. От определения этих коэффициентов во многом будет зависеть степень приближения модели к действительности.

Определим коэффициенты двух блоков («Диффузия» и «Радиация») первого варианта модели. Расчетные модели для 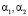определяются непосредственно из системы уравнения:

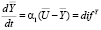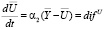;, фиксируя время 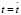[4]:

.

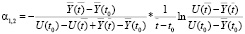Для определения 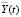привлечется непрерывная модель диффузии.

Параметры rk, ak, hk, pk, ek, для чистой влажной атмосферы можно рассчитать с помощью следующих формул полученных [2]:

,

,

,

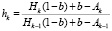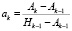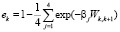где

,

, ,

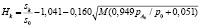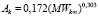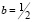где: s0 – поток прямой радиации на верхней границе атмосферы (солнечная постоянная); sk – поток прямой радиации на уровне с давлением; pAk, p0 – давление у поверхности земли; M = f(h0) – число оптических масс атмосферы, где h0 – высота Солнца; Ak – функция поглощения прямой солнечной радиации водяным паром; Wk? – содержание водяного пара в столбе единичного сечения с основаниями k, ∞ (в г/см2): 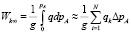, где: ek – функция поглощения длинноволнового излучения водяным паром; Wk,h + 1 – содержания водяного пара в столбе единичного сечения с основаниями k, k+1; β1 = 0,166, β2 = 2,60, β3 = 36,2, β4 = 114.

Вычислительный эксперимент реализации на ЭВМ численных расчетных моделей переноса и диффузии примеси в пограничном слое атмосферы и по его результатам построение геоэкологической карты загрязненности орографии местности на примере Карачаганакского нефтегазоконденсатного месторождения.

Моделировался суточный ход температуры в одной ячейке модели в летний, безоблачный, безветренный день для широты 55,7° и склонения Солнца 23,4°. Поверхность считалась достаточно увлажненной (q0 = qНАС (Т0)) с коэффициентом отражения (альбедо) r = 0,2. Твердые и газообразные примеси не учитывались. Задавалось начальное состояние:

Т_-1 = 287, Т₀ = 283, q₁ =285, q₂ =282, q₃ =260, q₁ = 0,0054, q₂ = 0,0045, q₃ = 0,0014.

Система уравнений (1) интегрировалась методом Рунге-Кутта с шагом по времени t = 1 ч. Результаты расчетов сравнивались с данными экспедиционных наблюдений.

Экстренные дополнительные источники загрязнение природных сред

Основные причины аварий на объектах магистральных трубопроводов представлены на рис. 4.

Объемы аварийных утечек на магистральном трубопроводном транспорте нефти в 1999–2001 гг. составили соответственно 1332, 512 и 1530 м3.

Из-за внешних воздействий на нефтепроводах происходит более 5 % аварий от общего их числа, а по наносимому ущербу они занимают первое место (рис. 4).

Рис. 1. Авария на нефтегазовом комплексе

Рис. 2. Авария на трубопроводе сопровождение с пожаром

Рис. 3. Пожар на нефтяной скважине

Рис. 4. Разлив нефти из-за трещин на трубопроводе

Произведен вычислительный эксперимент реализации расчетных моделей переноса и диффузии примеси в пограничном слое атмосферы и по его результатам построение геоэкологической карты загрязненности орографии местности в конвективных условиях и в инверсионных условиях. Распространение примесей в устойчивых атмосферных условиях, проводилось для двух вариантов: в первом случае скорость ветра в приземном слое выбрана равная 2 м/с , а во втором – 4 м/с.

Время расчета, соответствовало периоду полного продувание района месторождения, имеющего протяженность порядка 40 км.

Библиографическая ссылка