Не без влияния геополитических коллизий в энергетике осенью 2014 года все СМИ обрушили на мировую общественность поток рекламы холодного термоядерного синтеза Андреа Росси, например сайт http://ari.ru/news/2014/10/18/verificirovan-reaktor-holodnogo-termoyadernogo-sinteza-andrea-rossi » НОВОСТИ » Верифицирован реактор холодного термоядерного синтеза Андреа Росси. Эти «НОВОСТИ» воскресили прежние сайты, например: http://newsland.com/news/detail/id/818079/ и др., что 28 октября 2011 года продана первая установка холодного термоядерного синтеза. Вместе с этим, здесь можно вспомнить, что после многочисленных публикаций в научно-популярных журналах «Техника-Молодёжи» №7/1989, №8/1989, №8/1991, «Изобретатель и Рационализатор» №2/1990, №3/1991 и др. о зарубежных и отечественных разработках по этой проблеме научное издательство УРО РАН в 2003 году выпустило в свет брошюру «Взаимопревращения химических элементов», В.Ф. Балакирев, В.В. Крымский, Б.В. Болотов и др. Под ред. В.Ф. Балакирева. Екатеринбург: УРО РАН, 2003. 64 с.[1], из аннотации в которой цитирую: «…Приведены пять способов воздействия, дающих качественно похожие результаты. Процессы превращения сопровождаются выделением энергии. Общий характер воздействия разных способов связан с большими импульсными токами и импульсными полями. В основном представлены два вида сред, которые подвергаются воздействию: расплавы металлов и водные среды…», при этом обращая внимание на последние, подчёркнутые слова.
I. Магнитодинамическое введение
В попытках выйти из своих противоречий классическая электродинамика вводит надуманный векторный потенциал, подчиняя его произвольным требованиям
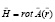 (1)
(1)
и
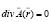 , (2)
, (2)
которые к желаемым результатам не привели. Релятивистская физика, пытаясь рассматривать магнитное и электрическое поля в четырёхмерном пространстве, в своих дифференциальных преобразованиях применяет к ним так называемый четырёх – вектор, получая результаты:
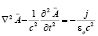 (3)
(3)
и 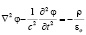 , (4)
, (4)
которые по прежнему означают раздельные магнитное и электрическое поля, так и не выйдя из тупиков и парадоксов классической электродинамики [3]. Другими словами, классическая электродинамика в действительности была основана не на четырёх уравнениях Максвелла:
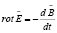 , (5)
, (5)
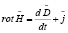 , (6)
, (6)
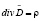 , (7)
, (7)
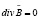 , (8)
, (8)
а на трех аксиомах, поэтому могла решать лишь плоские задачи, то есть для нее оказалось невозможным решение задач в трехмерном пространстве («электромагнитный парадокс», взаимодействие тороидальных обмоток, взаимодействие длинных соленоидов и др.). Магнитодинамика [2] заменила неадекватную аксиому (8) на адекватную и оказалась способной успешно решать трехмерные задачи на основе четырех адекватных аксиом. После замены в фундаментальной системе уравнений классической электродинамики неадэкватного положения, что
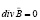 , (8)
, (8)
которое означает отсутствие источников магнитного поля, на соответствующий действительности принцип, что
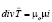 , (9) [3]
, (9) [3]
оказалось возможным не только снять «электромагнитный парадокс», но и решить многие теоретические проблемы электродинамики и практические задачи электротехники [3]. Таким образом, принимая за начало узловых этапов эволюции электродинамики даты фундаментальных открытий и изобретений из её истории, можно графически представить эволюцию электродинамики в полном соответствии с S-образным законом эволюции систем на рис. 1.
При этом невозможно проходить мимо удручающего факта, что суммарный эффект всех тех многих тысяч исследований пока равен нулю, так как на основе этих расчётов и проектов практика строит всё новые и новые, всё более гигантские монстры экспериментальных установок типа «ТОКАМАКОВ», «СТЕЛЛАТОРОВ», «ГИБРИДЕРОВ» и т.п., но с подозрительным постоянством всякий раз надежды экспериментаторов не оправдываются, принуждая распорядителей кредитов на многомиллиардные расходы по сооружению этих монстров публиковать в академической прессе (ПОИСК и др.) дежурные «оптимистические» отчёты, уподобляясь тем изобретателям «вечного двигателя», которым просто «не хватило мелочи», чтобы их колесо не останавливалось. Вместе с тем, так как два элемента тока взаимодействуют между собой по прямой линии подобно электрическим зарядам, то их взаимодействие можно характеризовать величиной магнитного натяжения:
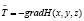 . (10)
. (10)
Другими словами, естественно положить в основу определения силовой характеристики магнитного поля величину и направление магнитной силы между токами согласно закону Ампера
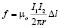 , (11)
, (11)
то есть для поля вокруг I1:
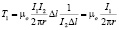 (12)
(12)
и для поля вокруг I2:
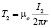 . (13)
. (13)
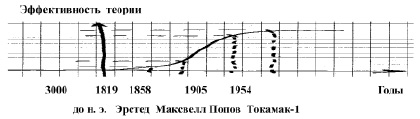
Рис. 1
II-1. Поле магнитного натяжения
Так как численное значение этой новой вектор – функции 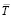 оказывается согласно выражениям (12) и (13) равным значению, которое ранее нами присваивалось величине напряженности магнитного поля по закону Био-Савара-Лапласа [2], то теперь магнитную напряженность H придется считать в соответствии с определением (10) скалярной величиной. Здесь уместно вспомнить, что по закону Био-Савара-Лапласа мы позволяли себе математический произвол, так как находя вектор
оказывается согласно выражениям (12) и (13) равным значению, которое ранее нами присваивалось величине напряженности магнитного поля по закону Био-Савара-Лапласа [2], то теперь магнитную напряженность H придется считать в соответствии с определением (10) скалярной величиной. Здесь уместно вспомнить, что по закону Био-Савара-Лапласа мы позволяли себе математический произвол, так как находя вектор 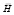 как векторное произведение векторов
как векторное произведение векторов 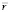 и
и 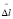 , должны были в соответствии с математическим определением векторного произведения исходить из их точки пересечения, но допускали «исключение из правила», «позволяя» вектору
, должны были в соответствии с математическим определением векторного произведения исходить из их точки пересечения, но допускали «исключение из правила», «позволяя» вектору 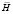 быть лишь ортогональным плоскости, образованной векторами – сомножителями
быть лишь ортогональным плоскости, образованной векторами – сомножителями 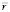 и
и 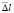 .
.
Раскроем определение (10):
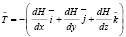 , (14)
, (14)
и для упрощения вычислений направим ток I по прямому проводу вдоль оси Z, тогда
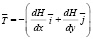 . (15)
. (15)
Для статического поля вектор – функции (1) самоочевидно соотношение 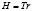 (16), которое полностью аналогично выражению для электростатического поля:
(16), которое полностью аналогично выражению для электростатического поля:
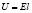 . (17)
. (17)
Симметричность геометрии магнитостатического и электростатического полей с этих позиций выявляется и в сравнении полей прямого провода с током по выражениям (12) и (13) с полем равномерно заряженной нити, величина которого может быть выражена аналогичной формулой
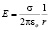 . (18)
. (18)
Ясно, что имея два провода с токами противоположного направления, получим геометрическую картину общего для них магнитного поля натяжением 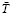 как на рис. 2.
как на рис. 2.
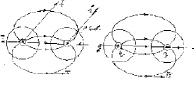
Рис. 2
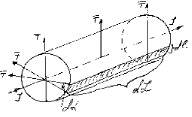
Рис. 3
Здесь отчетливо видно, что роль магнитного «монополя» в действительности выполняет электрический ток, создающий данное поле известная геометрическая картина электростатического поля как на рис. 2 представляется теперь мгновенным значением в результате сечения магнитного поля натяжением 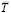 плоскостью, перпендикулярной токам, при соответствующей замене линий
плоскостью, перпендикулярной токам, при соответствующей замене линий 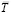 на линии
на линии 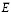 , а линий H на линии
, а линий H на линии 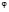 .
.
II-2. Уравнения поля
Разумеется, введение новой векторной функции 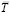 магнитного поля на основании реального направления магнитных сил вместе с адекватным отображением геометрии поля приводит к соответствующим изменениям вида уравнений Максвелла. Определяя величину потока магнитного натяжения
магнитного поля на основании реального направления магнитных сил вместе с адекватным отображением геометрии поля приводит к соответствующим изменениям вида уравнений Максвелла. Определяя величину потока магнитного натяжения 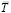 вокруг провода с током через замкнутую поверхность вокруг этого провода, представим элементарный поток
вокруг провода с током через замкнутую поверхность вокруг этого провода, представим элементарный поток
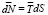 , (19)
, (19)
где dS – элемент поверхности около провода с токомкак на рис.3.
Так как dS = dL dl и dl = r dα, то вычисления дают:
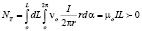 ; (20)
; (20)
Таким образом, поле магнитного натяжения 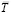 вокруг провода с током есть поле потенциальное, его силовая характеристика
вокруг провода с током есть поле потенциальное, его силовая характеристика 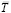 направлена по силам взаимодействия токов, создающих данное поле
направлена по силам взаимодействия токов, создающих данное поле 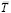 . При полной осевой симметрии магнитного натяжения
. При полной осевой симметрии магнитного натяжения 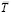 вокруг тока
вокруг тока 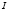 по прямому проводу вдоль оси Z очевидно:
по прямому проводу вдоль оси Z очевидно:
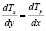 , (21)
, (21)
откуда сразу следует, что
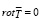 . (22)
. (22)
по аналогии с определением
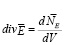 , (23)
, (23)
найдем и
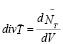 , (24)
, (24)
где NТ = 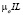 . (I-20).
. (I-20).
Рассмотрим случай стационарного тока I = Const
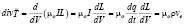 .(25)
.(25)
Так как 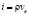 , то можно записать
, то можно записать
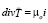 . (26)
. (26)
Сводя полученные результаты по (22) и (26) с известными уравнениями Максвелла для стационарного тока, получим систему
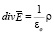 , (27)
, (27)
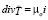 , (28)
, (28)
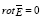 , (29)
, (29)
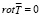 . (30)
. (30)
В случае статики, когда заряды неподвижны, уравнение (28) вырождается в уравнение (27), а уравнение (30) вырождается в уравнение (29), сводя таким образом систему уравнений к двум известным уравнениям электростатического поля как частного случая поля электромагнитного, что полностью соответствует действительности.
II-3. Электромагнитные силы
В силу наших определений (11) и (13) запишем
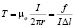 , (31)
, (31)
откуда легко видеть, что нахождение сил взаимодействия токов сводится к их вычислению по заданным токам в проводниках в известных полях магнитного натяжения 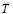 . Поэтому вопрос о взаимодействии проводников с токами сводится к нахождению их полей магнитного натяжения
. Поэтому вопрос о взаимодействии проводников с токами сводится к нахождению их полей магнитного натяжения 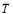 :
:
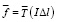 . (32)
. (32)
Так, например, силы действия сторон изогнутого провода с током друг на друга можно теперь представить как на рис. 4, из которого с очевидностью вытекает геометрическое соотношение для сил в поле магнитного натяжения 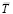 :
:
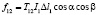 (33)
(33)
и 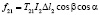 . (34)
. (34)
Но так как для данного случая самоочевидными являются тождества: I1ºI2 и T1ºT2, то из этого обстоятельства непосредственно следует вывод, что силы (33) и (34) друг друга взаимно компенсируют, так как
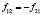 . (35)
. (35)
Поэтому в действительности на изогнутый провод с током действует лишь распрямляющая сила по (33) и (34), но нет никакой силы тяги для такой системы, что непосредственно снимает «электромагнитный парадокс». Аналогичные соображения относительно скрещенных проводов с токами приводят нас к выводу об их стремлении принять положение в одной плоскости, как это и происходит в действительности, что и показано на рис. 5.
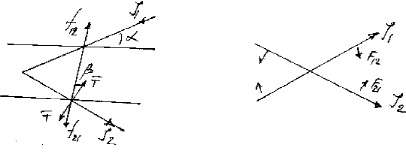
Рис. 4 Рис. 5
II-4. Практические рекомендации на основе магнитодинамики
В качестве иллюстраций возможностей изложенных выводов для оптимизации электромеханических систем здесь кратко отметим из десятков изобретений на их основе несколько наиболее практичных технических решений:
Как выяснилось, объективно-историческая ошибка в направлении силовой характеристики электромагнитного взаимодействия токов, привнесенная опытами Х. Эрстеда и вошедшая в фундаментальную систему уравнений Максвелла значительно затруднила технические решения в электротехнике. Действительно, самоочевидный вывод магнитодинамики об электромагнитной индукции при изменении магнитного натяжения вблизи проводника с изменением тока во времени:
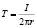 , (35)
, (35)
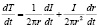 . (36)
. (36)
К сказанному по выражениям для ЭДС электромагнитной индукции (36) можно добавить, что величина ЭДС состоит из двух частей:
ЭДС=ЭДС1+ЭДС2, (37)
где
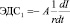 , (38)
, (38)
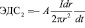 . (39)
. (39)
Ясно, что ЭДС1 возникает вследствие изменения тока I со временем, а ЭДС1 возникает в результате взаимодействия вторичного тока I2 с первичным I1 при изменении расстояния между ними. Данное обстоятельство, выраженное в зависимости (39) необходимо отметить здесь особенно. Дело в том, что с позиций классической электродинамики эта функциональная зависимость не является самоочевидной, а нами выше она выявлена уже по заранее эмпирически известному выводу (38). Но зависимость
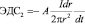
означает принципиальную возможность создания сверхвысоких напряжений в непосредственной близости от первичных проводников с переменными токами. Так, например, электролиты, проводимость которых на 5 – 6 порядков меньше проводимости металлических проводников, традиционной электротехникой не рассматриваются в качестве возможных электрических цепей. Вместе с тем, из выражения (39) непосредственно следует, что при погружении первичной обмотки в электролит возможно образовать в нем значительные токи и, следовательно, вызвать заметные электромагнитные (см. патенты РФ№2041779, №2026768 и др.) электромеханические(см. патенты РФ № 1424998, №1574906 и др.) или электрохимические (см. патенты РФ№2147555, № 2197550 и др.) эффекты. Отдельное пояснение здесь надо сделать относительно плотности тока, индуцированного обмоткой в электролите, которое иллюстрируется на рис. 6 и рис. 7. на рис. 6 показан разрез погруженной в электролит обмотки с выводами Н и К, подключенных к источнику переменного тока, в результате чего сам электролит вокруг обмотки представляет собой вторичный кольцевой (короткозамкнутый) виток проводника сечением S, в котором индуцируется вторичный ток плотностью i, зависящий от расстояния до первичной обмотки, как это показано на рис. 7. Другими словами, принципиально возможен подвод электромагнитной энергии магнитодинамическим способом в заданную область сплошной среды. Этот вывод и продемонстрирован ниже на изобретениях автора.
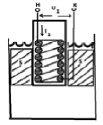
Рис. 6
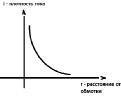
Рис. 7
III. Кольцевой магнито-динамический электролизёр автора по патенту №2197550 РФ на устройство для выплавки алюминия
Между тем, на основе магнитодинамики [3] можно предложить ряд установок не только для переплавки алюминия по патенту №2197550 РФ [4], но и для производства алюминиевых труб по патенту № 2026768 РФ [5] и др. Устройство и работа магнито-динамического электролизёра по патенту №2197550 РФ [4] представлена на рис. 8 и рис. 9, на которых представлены разрез электролизера вертикальной плоскостью и сечение по А-А. Цифровыми позициями на – указанных рисунках обозначены: 1-цилиндрический корпус магнитопровода, 2 – осевой стержень магнитопровода, 3 и 4 – дисковые верхний и нижний основания магнитопровода, 5 и 6 – цилиндрические обмотки из трубчатого провода, 7 – жаростойкая электро- и термоизоляция, 8, 9 и 10 – патрубки-каналы для загрузки и извлечения компонентов и продуктов выплавки алюминия. Действительно, при включении электропитания обмоток индуктора в металле на дне ванны индуцируются короткозамкнутые контуры электрического тока, энергия которых выделяется в виде теплоты, расплавляя металл и поддерживая заданную рабочую температуру расплава, в котором под действием электротока протекают электрохимические реакции до образования сплава заданных состава и свойств.
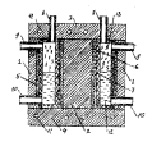
Рис. 8 (рис. IV-1 по [3])
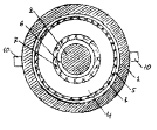
Рис. 9 (рис.IV-2 по [3])
IV. Проточный магнитодинамический электролизёр автора по патенту № 2147555 РФ на магнитодинамический аппарат для производства гидроксида натрия электрохимическим способом на переменном токе
Заявленной технической задачей, на решение которой направлено данное изобретение, является производство гидроксида натрия электрохимическим способом на переменном токе при полной механизации и автоматизации технологического процесса получения гидроксида натрия. на рис. 1. показана технологическая схема магнитодинамического аппарата для производства гидроксида натрия электрохимическим способом на переменном токе. Магнитодинамический аппарат для производства гидроксида натрия электрохимическим способом на переменном токе [6] включает в себя систему магнитодинамических электролизеров 1, приемник соляной кислоты 2, приемник каустической соды 3, накопитель соляной кислоты 4, трубопроводную магистраль с коллектором подвода рассола поваренной соли 5 к магнитодинамическим электролизерам 1, трубопроводную магистраль 6 с коллектором для сбора и отвода хлора и водорода из магнитодинамических электролизеров 1 в приемник соляной кислоты 2, трубопроводная магистраль 7 для отвода соляной кислоты в накопитель 4 с выводным патрубком 8, трубопроводная магистраль с коллектором 9 для отвода каустической соды из магнитодинамических электролизеров 1 в приемник 3 с выводным патрубком 10, линия электропередачи тока переменного 11 от блока электропитания 12 к магнитодинамическим электролизерам 1. на рис. 2. показан разрез магнитодинамического электролизера вертикальной плоскостью. Магнитодинамический электролизер 1 состоит из металлического тупикового стакана 13, электрически соединенного с металлическим проточным стаканом 14 токоотводящими лепестками 15. Стакан 14 вместе с коаксиально размещенным в нем стаканом 13 укреплены с помощью отбортовки 16 болтовыми креплениями 17 к электроизолирующей крышке 18. Входной трубчатый проводник 19 укреплен коаксиально внутри стакана 13 с помощью токоотводящих лепестков 20, приваренных к болтовому соединению 21 проводника 19 со стаканом 13. Вывод стакана 14 и трубчатый проводник 19 снабжены кольцевыми хомутами с клеммами 22 и 23 для подсоединения линии электропитания электролизера. Вывод стакана 14 и ввод трубчатого проводника 19 снабжены штуцерами 24 и 25 для присоединения гидролиний согласно технологической схеме. В крышке 18 выполнен трубопроводный вывод 26 для газообразных хлора и водорода. Герметизация элетролизера обеспечивается прокладкой 27 между отбортовкой 16 стакана 14 и крышкой 18. Количество электролизеров 1 в аппарате по конкретному условию эксплуатации может быть произвольным и определяется заданной производительностью аппарата. Количество тупиковых стаканов 13 и проточных стаканов 14 в каждом электролизере 1 может быть произвольным и определяется по конкретным условиям эксплуатации заданной концентрации каустической соды на выходе из аппарата. Габаритные размеры стаканов 13, 14 и трубчатого проводника 19 и толщина их стенок определяется заданной мощностью аппарата по конкретным условиям эксплуатации и ничем не ограничены.
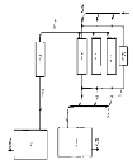
Рис. 10 (фиг.1 по [6])
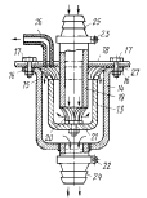
Рис. 11 (фиг. 2 по [6])
Устройство магнитодинамического электролизера по описанию обеспечивает электрическое соединение коаксиальных стаканов 13 и 14 и трубчатого проводника 19 между собой согласно по магнитному полю и последовательно по гидропотоку обрабатываемого рассола. Под воздействием переменных электротоков термодинамическое равновесие в растворе электролита нарушается, так как дополнительно к ионам диссоциированной поваренной соли образуются вследствие электролиза воды ее ионы водорода и гидроксидной группы.
V. Выводы
1. Вывод магнитодинамики о зависимости ЭДС от (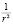 ) позволяет осуществлять подвод электромагнитной энергии в область сплошных сред.
) позволяет осуществлять подвод электромагнитной энергии в область сплошных сред.
2. Кольцевой магнитодинамический электролизёр по патенту РФ №2197550 обеспечивает возможность подведения электромагнитной энергии в область расплава.
3. Проточный магнитодинамический электролизёр по патенту РФ № 2147555 Обеспечивает возможность подведения электромагнитной энергии в область раствора.
Библиографическая ссылка
Вертинский П.А. К МАГНИТОДИНАМИКЕ УСТРОЙСТВА И РАБОТЫ УСТАНОВОК ХОЛОДНОГО ТЕРМОЯДЕРНОГО СИНТЕЗА // Международный журнал экспериментального образования. 2015. № 2-3. С. 452-458;URL: https://expeducation.ru/ru/article/view?id=6762 (дата обращения: 01.01.2026).

