Ошибки, допускаемые обучающимися при решении логарифмических уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера. об этих и других ошибках пойдет речь в этой статье.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних коней.
Рассмотрим на конкретных примерах ошибки подобного рода, но прежде обращаем внимание читателя на следующую мысль: не бойтесь приобрести посторонние корни, их можно отбросить путем проверки, бойтесь потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
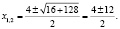
x1 = –4; x2 = 8.
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение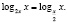 
Область определения исходного уравнения задается системой
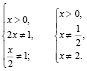
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
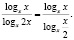
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению. Остановимся в связи с этим на примере.
Решить уравнение
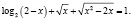
Найдем область определения этого уравнения, для чего решим систему неравенств:
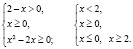
Откуда имеем x = 0. Проверим непосредственной подстановкой, является ли число x = 0 корнем исходного уравнения
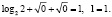
Ответ: x = 0.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Подтвердим сказанное следующим примером.
Решить уравнение
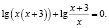
Приведем ошибочное решение этого уравнения:
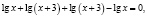
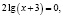
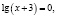
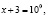
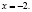
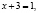х = –2.
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Проанализируем, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению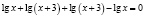 
эти же выражения могут быть только положительными. Следовательно, произошло сужение области определения, что и привело к потере корней.
Чтобы избежать потери корня, можно поступить следующим образом: перейдем в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Покажем это на примере.
Решить неравенство
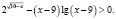
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
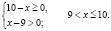
Для всех x из промежутка (9;10] выражение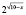 
имеет положительные значения (значения показательной функции всегда положительны).
Для всех x из промежутка (9;10] выражение x – 9 имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение (– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x∈ (9;10]. Заметим, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
Решить уравнение
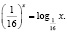
Наш опыт показывает, что учащиеся, решая это уравнение графически (заметим, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
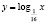и 
−
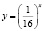это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень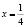 
и третий корень 
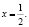Убедиться в справедливости сказанного можно непосредственной подстановкой чисел 
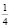и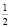 
в заданное уравнение.
Заметим, что уравнения вида logax = ax при 0 < a < e-e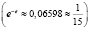 
всегда имеют три действительных корня.
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции разномонотонны (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Покажем типичные ошибки такого рода.
а) Решить уравнение xx = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
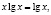
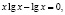
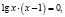
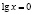или 
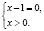
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее мы потеряли два корня уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
б) Решить уравнение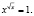 
Как и в предыдущем случае, мы имеем показательно-степенную функцию, а значит x > 0, x ≠ 1.
Для решения исходного уравнения прологарифмируем его обе части по любому основанию, например, по основанию 10: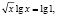 
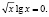
Учитывая, что произведение двух множителей равно нулю тогда, когда хотя бы один из них равен нулю, а другой при этом имеет смысл, мы имеем совокупность двух систем:
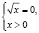или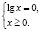 
Первая система не имеет решения; из второй системы мы получаем x = 1. Учитывая наложенные ранее ограничения, число x = 1 не должно являться корнем исходного уравнения, хотя непосредственной подстановкой мы убеждаемся в том, что это не так.
7. Рассмотрим некоторые ошибки, связанные с понятием сложной функции вида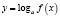 
. Ошибку покажем на таком примере.
Определить вид монотонности функции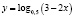 
.
Наша практика показывает, что абсолютное большинство учащихся определяют монотонность в данном случае лишь по основанию логарифма, а так как 0 < 0,5 < 1, то отсюда следует ошибочный вывод – функция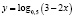 
убывает.
Нет! Эта функция возрастающая.
Условно для функции вида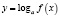 
можно записать:
– Возрастающая (Убывающая) = Убывающая;
– Возрастающая (Возрастающая) = Возрастающая;
– Убывающая (Убывающая) = Возрастающая;
– Убывающая (Возрастающая) = Убывающая;
8. Решите уравнение
.
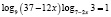Это задание взято из третьей части ЕГЭ, которое оценивается баллами (максимальный балл – 4).
Приведем решение, которое содержит ошибки, а значит за него не будет выставлен максимальный балл.
Сводим логарифмы к основанию 3. Уравнение примет вид
.
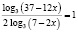Отсюда
,
.
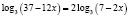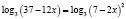Потенцируя, получаем
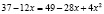или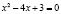 
,
х1 = 1, х2 = 3.
Выполним проверку, чтобы выявить посторонние корни
x = 1:
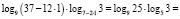
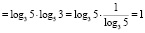, 1 = 1,
значит х = 1 – корень исходного уравнения.
х = 3:
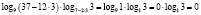, 0 ≠ 1,
значит х = 3 корнем исходного уравнения не является.
Поясним, почему это решение содержит ошибки. Суть ошибки в том, что запись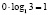 
, содержит две грубые ошибки. Первая ошибка: запись 
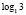вообще не имеет смысла. Вторая ошибка: не верно, что произведение двух сомножителей, один из которых 0, обязательно будет нулем. Ноль будет в том и только в том случае, если один множитель – 0, а второй множитель имеет смысл. Здесь же, как раз, второй множитель смысла не имеет.
9. Вернемся к уже прокомментированной выше ошибке, но при этом приведем и новые рассуждения.
При решении логарифмических уравнений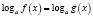 
переходят к уравнению 
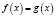. Каждый корень первого уравнения является корнем и второго уравнения. Обратное, вообще говоря, неверно, поэтому, переходя от уравнения 
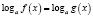к уравнению 
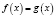, необходимо в конце проверить корни последнего подстановкой в исходное уравнение. Вместо проверки корней целесообразно заменять уравнение 
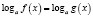равносильной системой
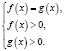
Если при решении логарифмического уравнения выражения
, 
, 
,
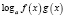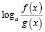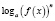где n – четное число, преобразовываются соответственно по формулам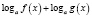 
, 
, 
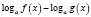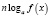, то, так как во многих случаях при этом сужается область определения уравнения, возможна потеря некоторых его корней. Поэтому указанные формулы целесообразно применять в следующем виде:
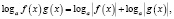
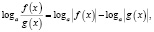
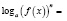
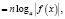
n – четное число.
Обратно, если при решении логарифмического уравнения выражения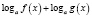 
, 
, 
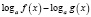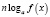, где n – четное число, преобразовываются соответственно в выражения
, 
, 
,
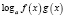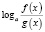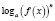то область определения уравнения может расшириться, в силу чего возможно приобретение посторонних корней. Помня об этом, в подобных ситуациях необходимо следить за равносильностью преобразований и, если область определения уравнения расширяется, делать проверку получаемых корней.
10. При решении логарифмических неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше, на стадии нахождения корней рациональной функции, получившейся в левой части неравенства. Этого делать не следует.
11. Приведем пример еще одной ошибки, связанной с решением неравенств.
Решите неравенство
.
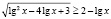Приведем ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
,
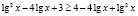откуда получаем неверное числовое неравенство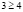 
, что позволяет сделать вывод: заданное неравенство не имеет решений.
Однако полученный вывод неверен, например, при х = 1000 имеем
, 
, 
.
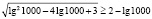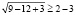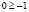Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Приведем правильное решение. Найдем область определения исходного неравенства. Она задается системой
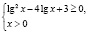или 
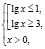
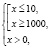откуда 
.
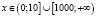Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а)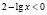 
, откуда х > 100. С учетом области определения исходного неравенства имеем промежуток 
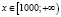. Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что 
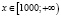– решение заданного неравенства.
б)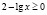 
, откуда 
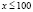. С учетом области определения исходного неравенства имеем промежуток 
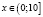. Для всех х из промежутка 
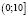имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь: 
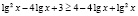, откуда 
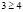. Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка 
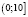решениями исходного неравенства не являются.
Ответ: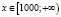 
.
12. Типичная ошибка при решении логарифмических уравнений, неравенств и их систем состоит в том, что неверно преобразовываются логарифмические выражения, входящие в них.
13. Часто допускаются ошибки при решении систем уравнений, в том числе и систем логарифмических уравнений, методом деления одного уравнения системы на другое.
Приведем пример такой ошибки, для чего указанным методом решим систему
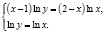
Разделив первое уравнение системы на второе, будем иметь
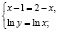
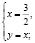
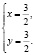
Но легко видеть, что и пара (1;1), которая удовлетворяет области определения системы уравнений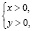 
также является решением системы. Действительно, подставляя х = 1 и у = 1 в исходную систему, имеем
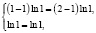откуда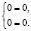 
Поясним, почему произошла потеря решения системы.
Если задана система двух уравнений с двумя неизвестными
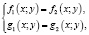
из которой мы получаем
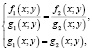
то вторая система уравнений будет следствием первой системы уравнений (значит содержит все решения первой системы) в том и только в том случае, когда нет ни одной пары (х; у), при которой бы функци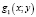и 
и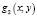 
одновременно обращались бы в ноль.
Как мы видим, такая пара (1; 1) в данном случае нашлась, потому-то и произошла потеря решения.
Более глубокий анализ этих и других ошибок читатель найдет в наших работах [2, 3, 4, 5].
Библиографическая ссылка
Далингер В.А. ТИПИЧНЫЕ ОШИБКИ УЧАЩИХСЯ ПРИ РЕШЕНИИ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ, НЕРАВЕНСТВ И ИХ СИСТЕМ И ПУТИ ИХ ПРЕДУПРЕЖДЕНИЯ // Международный журнал экспериментального образования. – 2015. – № 4-2. – С. 445-450;URL: https://expeducation.ru/ru/article/view?id=7437 (дата обращения: 20.04.2024).