Построение математических моделей многомассовых крутильных колебательных систем с сосредоточенными массами, к которым приводятся многие расчетные схемы технологических машин, связано с созданием общих динамических моделей системы и локальных моделей исполнительных или передаточных кулачково-рычажных механизмов с нелинейными функциями положения. К многомассовым крутильно-колебательным системам относятся системы с сосредоточенными параметрами, соединенными между собой упругими безмассовыми участками валов. Эти системы могут быть цепные, а также разветвленные с постоянными и периодически изменяемыми параметрами [I]. При составлении динамической модели исходят из предположений, что инерционные свойства системы отображаются массами mij или Jij сосредоточенными в сечениях, которые соединены без инерционными, упруго-диссипативными связями с жесткостью cij. Движение такой многомассовой крутильной системы описывается системой уравнений вида
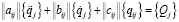 . (1)
. (1)
Здесь 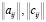 – матрицы инерционных и квазиупругих коэффициентов, qi – обобщенные координаты,
– матрицы инерционных и квазиупругих коэффициентов, qi – обобщенные координаты, 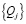 – матрицы обобщенных сил.
– матрицы обобщенных сил.
Инерционные коэффициенты aij каждого приводимого к общему валу механизма зависят от значений, приведенных к ним моментов инерции, отдельных механизмов, т.е. 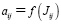 . Значения приведенных моментов инерции
. Значения приведенных моментов инерции 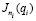 определяются методом приведения масс из условия равенства кинетических энергий для каждого положения приводимого механизма, определяемого обобщенной координатой qi звена приведения. При построении математической модели таких систем возникает необходимость, связанная с утомительным экспериментально-расчетным вычислением приведенных инерционных параметров многих передаточных и исполнительных механизмов. В быстроходных машинных агрегатах используются шарнирно-рычажные механизмы с существенно упругими звеньями. Процесс закручивания упругих валов или сжатия пружин осуществляется за счет передаточных механизмов под действием движущего момента со стороны двигателя. Процесс разрядки происходит под действием потенциальных энергии закрученных валов или сжатых пружин. При этом движение таких исполнительных механизмов с упругими звеньями не зависит от вращения главного вала машинного агрегата (механизмы независимого движения). Часто, приводимые к сечениям общей модели машин, передаточные или исполнительные механизмы представляют систему с одной степенью свободы с жесткими звеньями. Движение такого механизма описываются уравнением:
определяются методом приведения масс из условия равенства кинетических энергий для каждого положения приводимого механизма, определяемого обобщенной координатой qi звена приведения. При построении математической модели таких систем возникает необходимость, связанная с утомительным экспериментально-расчетным вычислением приведенных инерционных параметров многих передаточных и исполнительных механизмов. В быстроходных машинных агрегатах используются шарнирно-рычажные механизмы с существенно упругими звеньями. Процесс закручивания упругих валов или сжатия пружин осуществляется за счет передаточных механизмов под действием движущего момента со стороны двигателя. Процесс разрядки происходит под действием потенциальных энергии закрученных валов или сжатых пружин. При этом движение таких исполнительных механизмов с упругими звеньями не зависит от вращения главного вала машинного агрегата (механизмы независимого движения). Часто, приводимые к сечениям общей модели машин, передаточные или исполнительные механизмы представляют систему с одной степенью свободы с жесткими звеньями. Движение такого механизма описываются уравнением:
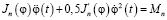 , (2)
, (2)
где j – угол поворота звена приведения.
В задачах динамического анализа и синтеза механизмов обычно исходят из идеальной модели машины, т.е. пренебрегают динамическими ошибками. Оценка динамических ошибок, определение неравномерности вращения ведущих звеньев, определение соотношений между массами и силами, обеспечивающих заданный режим движения, является одним из основных задач динамического анализа и синтеза. Для их решения используются более сложные модели машины, учитывающие упругости звеньев, характеристики двигателей и т.д.
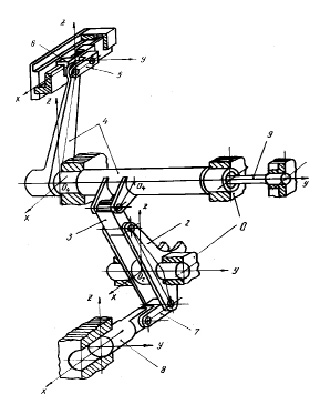
Рис. 1. Общий вид и конструкция боевого механизма станков-автоматов типа СТБ
Примером механизма независимого действия, в данной работе, является боевой механизм ткацкого станка-автомата типа СТБ предназначенный для прокладывания уточной нити. Движение гонков микрочелнока (рис. 1) осуществляется за счет потенциальной энергии закрученного торсионного вала 9, который закручивается на 300-320 посредством кулачкового механизма через трехплечий рычаг 2. В систему введено демпфирующее устройство 8, в виде масляного катаракта. В быстроходных машинных агрегатах используется шарнирно-рычажные механизмы с существенно-упругими звеньями. Процесс закручивания валов или сжатие пружин осуществляется за счет передаточных механизмов под действием движущего момента со стороны двигателя. Процесс разрядки происходит под действием потенциальных энергии закрученных валов или сжатых пружин. При этом движение таких исполнительных механизмов с упругими звеньями независимо от вращения главного вала машинного агрегата (механизмы независимого движения). Если при решении прямой задачи динамики механизмов в первом приближении можно предполагать, что все звенья абсолютно жесткие, которые дают достаточную для практики информацию об изменении параметров, то в решение второй задачи – динамического проектирования, нельзя не учитывать упругие свойства звеньев, силы трения, зазоры в кинематических парах и другие нелинейные характеристики механизма. Однако возникает необходимость решения и обратной задачи, когда заданы кинематические характеристики движения машины и необходимо найти оптимальные значения масс, моментов инерции, а следовательно и размеров звеньев, при которых механизмы нагружаемые заданными силами, осуществляли бы заданный закон движения.
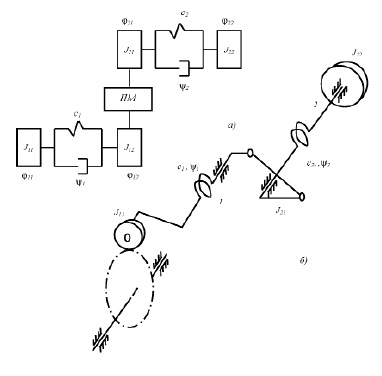
Рис. 2. Динамическая модель кулачково-рычажного механизма с упругими звеньями
На рис. 2. представлена динамическая модель кулачково-рычажного механизма с упругими звеньями, где Jij, ci, ϕi – постоянные моменты инерции звеньев, коэффициенты жесткости и диссипации; ПМ – передаточная функция.
Для механизмов с существенно упругими звеньями, т.е. для механизмов независимого движения предлагаем аналитический метод определения инерционных коэффициентов динамической модели машин с использованием уравнений движения отдельных приводимых к общему валу механизмов вида (2). Значения приведенных моментов сил могут быть определены известными методами для каждого приводимого механизма. Законы движения, без учета колебательных явлений, динамических ошибок входных звеньев отдельных механизмов определяются из характеристики двигателя и функции положения. Использованные уравнения движения исполнительных механизмов для определения приведенного момента инерции при построении общей динамической модели сложной машины удобно при изучении движения так называемых механизмов независимого действия. Такие механизмы, у которых основное движение осуществляется за счет моментов упругих сил закрученных валов или сжатых пружин, часто встречаются в текстильных машинах [2]. Действительно уравнение (2) может быть рассмотрено относительно функции 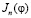 как линейное дифференциальное уравнение первого порядка с коэффициентами
как линейное дифференциальное уравнение первого порядка с коэффициентами 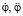 [3]. Например, движение механизма боя станка СТБ – автомата бесчелночных станков [2], в процессе зарядки (закручивания) торсионного вала, можно описывать уравнением:
[3]. Например, движение механизма боя станка СТБ – автомата бесчелночных станков [2], в процессе зарядки (закручивания) торсионного вала, можно описывать уравнением:
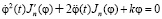 , (3)
, (3)
где 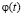 – угол поворота упругого вала, который определятся функцией положения механизма и характеристикой двигателя.
– угол поворота упругого вала, который определятся функцией положения механизма и характеристикой двигателя.
Закручивание упругих валов и сжатие упругих пружин, в быстроходных механизмах, осуществляется в течение сравнительно большего времени, чем времени разрядки упругих элементов. Движения исполнительных механизмов с конечно-деформируемыми звеньями, например, вал закручивается на 30-320, пружины сжимаются на 30-40 мм, определяются номинальной скоростью вращения главного вала машинного агрегата и функцией положения. Решив уравнение (3) при известных начальных условиях можно определить значения приведенного момента инерции механизма для каждого положения системы.
Действительно, дифференциальное уравнение первого порядка относительно приведенного момента инерции исполнительного механизма имеет вид:
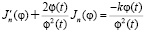 , (4)
, (4)
Решение уравнения (4) при 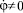 имеет вид:
имеет вид:
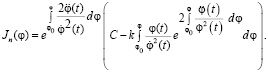
Вычисляя отдельно интеграл:
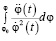 (5)
(5)
получим:
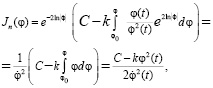 (6)
(6)
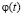 – определяется через функции положения между главным валом машинного агрегата и входным звеном исполнительного механизма с упругим звеном.
– определяется через функции положения между главным валом машинного агрегата и входным звеном исполнительного механизма с упругим звеном.
Постоянная интегрирования С и коэффициент K зависят от моментов инерции звеньев и движущих сил.
Поскольку положение механизма в процессе разрядки (раскручивания) под действием закрученного упругого вала соответствует его положению при зарядке, полученные значения приведенного момента инерции определяют инерционные характеристики системы при моделировании ее движения в процессе разрядки.
Таким образом, использование уравнения движения исполнительных и передаточных механизмов с существенно упругими звеньями позволяет автоматизировать построение математической модели многомассовых механических систем [4].
Библиографическая ссылка
Уалиев З.Г., Уалиев Г., Уалиева И.М. ДИНАМИКА МЕХАНИЗМОВ С СУЩЕСТВЕННО УПРУГИМ ЗВЕНОМ // Международный журнал экспериментального образования. 2015. № 8-3. С. 327-331;URL: https://expeducation.ru/ru/article/view?id=8134 (дата обращения: 18.11.2025).

