Известно, что распределение намагниченности по объему образца из магнитомягкого материала сложной формы, например в процессе работы электротехнического изделия постоянного тока [1] на его основе, часто бывает неоднородным. Неоднородности намагничивания способствует не только сложная форма, но и наличие внутренних дефектов, например инородных включений. Существующие подходы анализа работы электротехнических изделий постоянного тока не позволяют получить полную информацию о магнитном состоянии всех частей магнитомягкого материала и, следовательно, достоверно диагностировать работу изделия [2, 3]. Таким образом, важной становится задача нахождения распределения намагниченности по объему образца из магнитомягкого материала. Для решения поставленной задачи предлагается использовать выражение для магнитостатики, определяющее связь между вектором намагниченности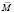 
и напряженностью 
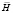созданного им поля в некоторой точке Q [4]:
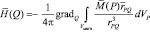, (1)
где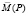 
– вектор намагниченности вещества в элементе объема образца dVP; dVP – элемент объема, содержащий точку P; 
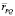– радиус-вектор, направленный от элемента объема образца P к точке наблюдения Q, причем модуль вектора 
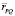равен:
,
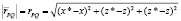где x*, y*, z* – координаты точки наблюдения Q; x, y, z – координаты элемента объема образца dVP.
Для численного решения уравнения (1) объем образца разбивается на n элементарных объемов, в пределах каждого из которых намагниченность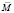 
с некоторым приближением можно считать постоянной. Зная напряженность внешнего магнитного поля в n различных точках, можно перейти от уравнения (1) к системе из 3n алгебраических уравнений вида:
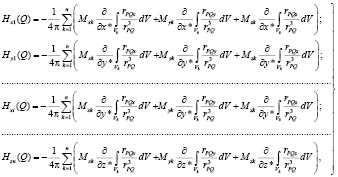(2)
где Hxi(Q), Hyi(Q), Hzi(Q) – соответственно проекции на оси напряженности внешнего магнитного поля в точке Q (x*, y*, z*); Mxk, Myk, Mzk – проекции намагниченности k-го элементарного объема образца; rPQx, rPQy, rPQz – проекции радиус-вектора, направленного от центра k-го элемента в точку наблюдения; i – номер точки наблюдения; k – номер элементарного объема, по которому выполняется интегрирование.
Таким образом, задача определения распределения намагниченности магнитомягкого материала в составе конкретного электротехнического изделия может быть решена путем составления и расчета системы уравнений (2). При этом, первоначально должна быть определена форма элементарных объемов, на которые разбивается образец, их количество, координаты измерительных преобразователей. Решение данных вопросов может быть сведено к классической оптимизационной задаче. Для ее решения предлагается использовать метод градиентного спуска [5], в котором факторами будут являться указанные выше параметры (форма элементарных объемов, их количество и координаты измерительных преобразователей), а функцией цели – минимум погрешности определения распределения намагниченности при минимуме числа элементарных объемов, на который разбивается образец. Проведение физических экспериментов для нахождения оптимальных параметров в данном случае не рекомендуется использовать, так как погрешность измерения значений напряженности магнитного поля с помощью существующих средств (для магнитных измерений составляет в основном не менее 5 %) будет вносить дополнительную неоднозначность решения системы уравнений (2). Для проведения экспериментов рекомендуется использование моделей электротехнических изделий, построенных на базе метода конечных элементов [6, 7].
Статья подготовлена по результатам работ, полученным в ходе выполнения проекта № СП-4108.2015.1, реализуемого в рамках программы «Стипендии Президента Российской Федерации молодым ученым и аспирантам, осуществляющим перспективные научные исследования и разработки по приоритетным направлениям модернизации российской экономики» на 2015-2017 гг.
Библиографическая ссылка
Шайхутдинов Д.В. ОПРЕДЕЛЕНИЕ РАСПРЕДЕЛЕНИЯ НАМАГНИЧЕННОСТИ ВНУТРИ ОБРАЗЦОВ ИЗ МАГНИТОМЯГКОГО МАТЕРИАЛА СЛОЖНОЙ ФОРМЫ ПО ЭКСПЕРИМЕНТАЛЬНО ОПРЕДЕЛЕННОЙ КАРТИНЕ ВНЕШНЕГО ПОЛЯ // Международный журнал экспериментального образования. – 2015. – № 11-1. – С. 37-38;URL: https://expeducation.ru/ru/article/view?id=8285 (дата обращения: 23.11.2024).