Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Мусаев В.К. 1

---

1 МГМУ

Приводится информация о моделировании нестационарных волн напряжений в деформируемых областях с помощью метода конечных элементов в перемещениях. Задачи решаются методом сквозного счета, без выделения разрывов. То есть применяется однородный алгоритм. За основные неизвестные в узле конечного элемента приняты два упругих перемещения и две скорости упругих перемещений. Основные соотношения метода конечных элементов в перемещениях по пространственным координатам получены с помощью принципа возможных перемещений, то есть с помощью метода динамического равновесия внутренних и внешних сил. Для аппроксимации по пространственным координатам применяются треугольные конечные элементы с линейной аппроксимацией упругих перемещений и прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. Для аппроксимации по временной координате применяются линейные конечные элементы с двумя узловыми точками с линейной аппроксимацией перемещений. При разработке комплекса программ использовался алгоритмический язык Фортран-90. Применяется квазирегулярный подход при аппроксимации исследуемой области. Рассмотрены следующие задачи. Рассматривается задача о воздействии плоской продольной упругой волны на свободное круглое отверстие. Рассматривается задача о воздействии плоской продольной упругой волны на свободное квадратное отверстие. Рассматривается задача о воздействии плоской продольной упругой волны на вырез треугольного профиля. Рассматривается задача о воздействии плоской продольной упругой волны на подкрепленное круглое отверстие. Рассматривается задача о воздействии плоской продольной упругой волны на подкрепленное квадратное отверстие.

Статья в формате PDF

2285 KB

динамика сплошных сред

распространение волн

волновая теория

полуплоскость

алгоритмический язык Фортран-90

численный метод

алгоритм

комплекс программ

конечные элементы первого порядка

условия на фронте плоской волны

импульсное воздействие

функция Хевисайда

напряжения на фронте плоской волны

свободное круглое отверстие

свободное квадратное отверстие

подкрепленное круглое отверстие

подкрепленное квадратное отверстие

вырез треугольного профиля

1. Мусаев В.К. Решение задачи дифракции и распространения упругих волн методом конечных элементов // Строительная механика и расчет сооружений. – 1990. – № 4. – С. 74–78.

2. Мусаев В.К. Численное моделирование динамического напряженного состояния сооружений уравнениями двумерной теории упругости и пластичности. Автореферат диссертации на соискание ученой степени доктора технических наук по специальности 01.02.04. – М.: Совинтервод, 1993. – 46 с.

3. Мусаев В.К. Численное решение волновых задач теории упругости и пластичности // Вестник Российского университета дружбы народов. Серия прикладная математика и информатика. – 1997. – № 1. – С. 87–110.

4. Мусаев В.К. Об оценке достоверности и точности численного решения нестационарных динамических задач // Вестник Российского университета дружбы народов. Серия проблемы комплексной безопасности. – 2007. – № 3. – С. 48–60.

5. Мусаев В.К. Оценка достоверности и точности результатов вычислительного эксперимента при решении задач нестационарной волновой теории упругости // Научный журнал проблем комплексной безопасности. – 2009. – № 1. – С. 55–80.

6. Мусаев В.К. О достоверности результатов математического моделирования нестационарных волн напряжений в объектах сложной формы // Строительная механика инженерных конструкций и сооружений. – 2014. – № 3. – С. 71–76.

7. Мусаев В.К. О достоверности компьютерного моделирования нестационарных упругих волн напряжений в деформируемых телах сложной формы // Международный журнал прикладных и фундаментальных исследований. –2014. – № 11. – С. 10–14.

8. Мусаев В.К. Моделирование нестационарных упругих волн напряжений в деформируемых областях с помощью метода конечных элементов в перемещениях // Современные наукоемкие технологии. – 2014. – № 12 (1). – С. 28–32.

9. Мусаев В.К. Оценка точности и достоверности численного моделирования при решении задач об отражении и интерференции нестационарных упругих волн напряжений // Успехи современного естествознания. – 2015. – № 1 (часть 7). – С. 1184–1187.

10. Мусаев В.К. Численное решение задачи о распространении нестационарных упругих волн напряжений в подкрепленном круглом отверстии // Современные наукоемкие технологии. – 2015. – № 2. – С. 93–97.

В настоящее время активно применяются численные методы для решения различных задач в области распространения волн напряжений в строительных объектах при нестационарных сейсмических воздействиях. Рассматриваемые физические процессы решаются с помощью методов математического моделирования, который в настоящее время является одним из мощных инструментов исследования.

Некоторые результаты в области целого комплекса проблем волнового воздействия на сооружения с окружающей средой рассмотрены в следующих работах [1–10].

Для решения краевой задачи используется метод конечных элементов в перемещениях. Задачи решаются методом сквозного счета, без выделения разрывов (однородный алгоритм). Решение двумерной плоской динамической задачи теории упругости с начальными и граничными условиями осуществляем с помощью метода конечных элементов в перемещениях. Для решения поставленной задачи используем метод конечных элементов в перемещениях. Основные соотношения метода конечных элементов получены с помощью принципа возможных перемещений. Чтобы выполнить динамический расчет методом конечных элементов, нужно иметь матрицу жесткости и матрицу инерции конечного элемента.

Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для некоторого тела, записываем приближенное значение уравнения движения в теории упругости

, ,

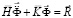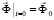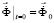, (1)

где 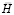– матрица инерции; 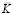– матрица жесткости; 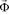– вектор узловых упругих перемещений; 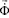– вектор узловых упругих скоростей перемещений; 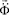– вектор узловых упругих ускорений; 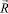– вектор узловых упругих внешних сил.

Соотношение (1) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.

Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями привели к линейной задаче Коши (1).

Рассмотрим интегрирование системы линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.

Для интегрирования уравнения (1) конечноэлементным вариантом метода Галеркина приведем его к следующему виду

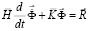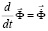, . (2)

Интегрируя по временной координате соотношение (2) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек

,

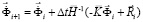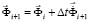, (3)

где 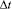– шаг по временной переменной.

Шаг по временной переменной 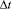определяем из следующего соотношения

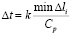, (4)

где 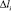– длина стороны конечного элемента; C_p – скорость распространения продольной волны.

Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной схемы.

На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных динамических воздействиях на сооружения.

Некоторая информация о достоверности разработанного численного метода, алгоритма и комплекса программ приведена в следующих работах [1–7, 9–10].

1. Рассматривается задача о воздействии плоской продольной упругой волны на свободное круглое отверстие. Начальные условия приняты нулевыми.

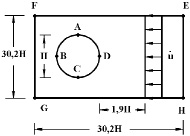
Рис. 1. Постановка задачи для свободного круглого отверстия

В сечении на расстоянии 1,9Н (рис. 1) при 0 ≤ n ≤ 10 (n = t/∆t) скорость упругого перемещения изменяется линейно от 0 до P (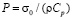 ( 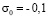МПа)), а при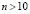 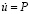. Контур круглого отверстия АBCD предполагается свободным от нагрузок при t > 0. Граничные условия для контура EFGH при t > 0 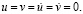Отраженные волны от контура EFGH не доходят до исследуемых точек при 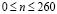. Расчеты проведены при следующих исходных данных: H = 0,18 м; ∆t = 0,407·10^-5 c; E = 0,36·104 MПа; n = 0,36; r = 0,122·104 кг/м³; С_r = 1841 м/с. Исследуемая расчетная область имеет 1536 узловых точек. Контур круглого отверстия аппроксимирован 28 узловыми точками.

2. Рассматривается задача о воздействии плоской продольной упругой волны на свободное квадратное отверстие. Начальные условия приняты нулевыми.

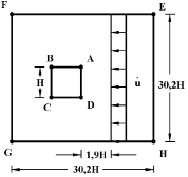
Рис. 2. Постановка задачи для свободного квадратного отверстия

В сечении на расстоянии 1,9H (рис. 2) при 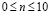скорость упругого перемещений изменяется линейно от 0 до Р, а при n > 10 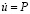( (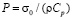 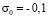МПа)). Контур квадратного отверстия АBCD предполагается свободным от нагрузок при t > 0. Граничные условия для контура EFGH при t > 0 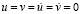. Отраженные волны от контура EFGH не доходят до исследуемых точек при 0 ≤ n ≤ 200. Исследуемая расчетная область имеет 1337 узловых точек.

3. Рассматривается задача о воздействии плоской продольной упругой волны на вырез треугольного профиля. Начальные условия приняты нулевыми. В сечении на расстоянии 1,8H (рис. 3) при 0 ≤ n ≤ 10 скорость упругого перемещения изменяется линейно от 0 до Р, а при n > 10 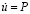((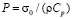 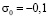МПа (–1 кгс/см²))). Контур выреза ABCDEF (кроме точки B) предполагается свободным от нагрузок при t > 0. Граничные условия для контура FGHA при 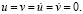Отраженные волны от контура FGHA не доходят до исследуемых точек при 0 ≤ n ≤ 200. Исследуемая расчетная область имеет 1464 узловых точек.

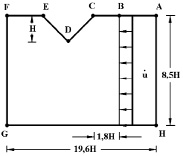
Рис. 3. Постановка задачи для выреза треугольного профиля

4. Рассматривается задача о воздействии плоской продольной упругой волны на подкрепленное круглое отверстие. Начальные условия приняты нулевыми. В сечении на расстоянии 1,6H (рис. 4) при 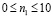(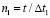) скорость упругого перемещения 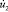изменяется линейно от 0 до 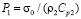, а при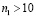 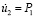( 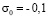МПа). Внутренний контур подкрепленного отверстия ABCD предполагается свободным от нагрузок при t > 0. На границе подкрепления и среды EFGH приняты условия непрерывности перемещений. Граничные условия для контура IJKL при t > 0 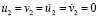. Отраженные волны от контура IJKL не доходят до исследуемых точек при .

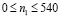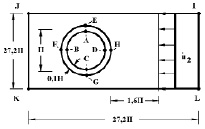
Рис. 4. Постановка задачи для подкрепленного круглого отверстия

Расчеты проведены при следующих исходных данных: H = 0,2 м; ∆t₁ = 0,186·10^-5 c; E₁= 0,72·10⁵ MПа; ν₁= 0,3; ρ₁= 0,275·10⁴ кг/м³; С_p1 = 5364 м/с; ∆t₂ = 0,407·10^-5 c; E₂ = 0,36·10⁴ MПа; ν₂ = 0,36; ρ₂ = 0,122 · 10⁴ кг/м³; С_p2 = 1841 м/с (…1 – подкрепление; …2 – среда).

Исследуемая расчетная область имеет 1536 узловых точек. Внутренний контур подкрепления аппроксимирован 28 узловыми точками. По толщине подкрепление аппроксимировано двумя узловыми точками.

5. Рассматривается задача о воздействии плоской продольной упругой волны на подкрепленное квадратное отверстие.

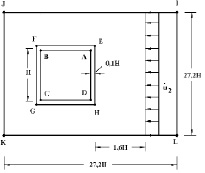
Рис. 5. Постановка задачи для подкрепленного квадратного отверстия

Начальные условия приняты нулевыми. В сечении на расстоянии 1,6H (рис. 5) при 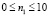скорость упругого перемещения 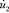изменяется линейно от 0 до 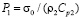, а при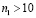 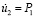( 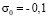МПа). Внутренний контур подкрепленного квадратного отверстия АBCD предполагается свободным от нагрузок при t > 0. На границе подкрепления и среды EFGH приняты условия непрерывности перемещений. Граничные условия для контура IJKL при t > 0 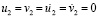. Отраженные волны от контура IJKL не доходят до исследуемых точек при 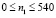. Исследуемая расчетная область имеет 1337 узловых точек.

Проведенные исследования позволяют сделать следующие выводы:

Рассмотрена постановка задачи о воздействии плоской продольной упругой волны на свободное круглое отверстие.

Рассмотрена постановка задачи о воздействии плоской продольной упругой волны на свободное квадратное отверстие.

Рассмотрена постановка задачи о воздействии плоской продольной упругой волны на вырез треугольного профиля.

Рассматривается постановка задачи о воздействии плоской продольной упругой волны на подкрепленное круглое отверстие.

Рассматривается постановка задачи о воздействии плоской продольной упругой волны на подкрепленное квадратное отверстие.

Методика, алгоритм, комплекс программ и результаты решенных задач рекомендуются для использования в научно-технических организациях, специализирующихся в области динамического расчета сооружений с окружающей средой.

Математическое моделирование позволяет учесть инженерные объекты при решении задач о безопасности территорий при нестационарных волновых сейсмических воздействиях.

Библиографическая ссылка