Тема «Интегральное исчисление функций нескольких переменных» занимает важное место в образовательном процессе в высшей школе. Она имеет большое значение, как в самой математике, так и широко используется при решении прикладных задач. При этом, чтобы сделать процесс математического моделирования изучаемых практических задач более наглядным и понятным оказываются полезными различные пакеты систем компьютерной математики, в частности, можно применить систему Maple.
Цель исследования. Рассмотреть возможности системы компьютерной математики Maple для вычисления кратных интегралов и решения прикладных задач.
Материал исследования. Рассмотрим несколько примеров, связанных с вычислением кратных интегралов или с их приложениями в геометрии, и покажем возможности решения данных заданий в системе Maple.
Пример 1. Вычислить интеграл
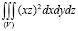 ,
,
где тело (V) ограничено поверхностями x = 2, y = 2x, y = 0, z = 0, z = xy.

Решение. Так как выполнение пространственных чертежей вручную весьма затруднительно, то воспользуемся компьютером для создания наглядного образа. Сначала попытаемся использовать одинаковый масштаб по осям координат:
> with(plots):
> with(student):
> A1:=plot3d([(2),(u),(v)],u=0..4,v=0..2*u,axes=normal):
> A2:=plot3d([(u),(2*u),(v)],u=0..2,v=0..(u^2)*2,axes=normal):
> A3:=plot3d([(u),(0),(v)],u=0..2,v=0..0,axes=normal):
> A4:=plot3d([(u),(v),(0)],u=0..2,v=0..2*u,axes=normal):
> A5:=plot3d([(u),(v),(u*v)],u=0..2,v=0..2*u,axes=normal):
> display({A1,A2,A3,A4,A5},labels=[x,y,z],scaling=constrained);
Как видно, этот подход не очень удачен. Поэтому для наглядности иллюстрации воспользуемся разным масштабом по осям координат:
> display({A1,A2,A3,A4,A5},labels=[x,y,z]);
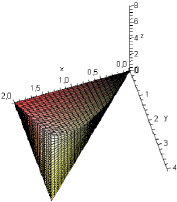
Область является правильной относительно всех осей. При проектировании тела на плоскость Оху получим:
> inequal({y<x*2,x=2,y=0},x=0..2,y=0..4,optionsfeasible=(color=green),optionsexcluded= (color=white),axes=normal,labels=[x,y],
scaling=CONSTRAINED);
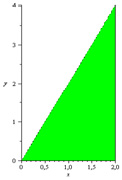
Исходный интеграл сводится к повторному:
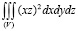 =
= 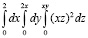 =
=
=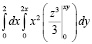 =
= 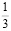
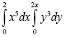 =
=
= 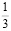
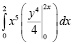 =
= 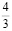
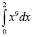 =
=
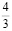
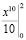 =
= 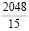 .
.
Вычисление интеграла в Maple происходит следующим образом:
> with(student):
> Tripleint((x*z)^2, z=0..x*y, y=0..2*x, x=0..2);
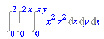
> value(%);
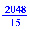
Пример 2. Вычислить объем прямого бруса, ограниченного сверху параболоидом 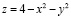 и имеющего основанием квадрат, ограниченный в плоскости Oxy прямыми x = ±1, y = ±1.
и имеющего основанием квадрат, ограниченный в плоскости Oxy прямыми x = ±1, y = ±1.
Решение. Прежде всего, делаем рисунок с помощью системы Maple:
> with(plots):
> with(student):
> A1:=plot3d([(u),(v),(4-u^2-v^2)], u=-1..1,v=-1..1,
axes=normal):
> A2:=plot3d([(u),(v),(0)],u=-1..1,v=-1..1,axes=normal):
> A3:=plot3d([(1),(u),(v)],u=-1..1, v=0..3-u^2,axes=normal):
> A4:=plot3d([(-1),(u),(v)],u=-1..1, v=0..3-u^2,axes=normal):
> A5:=plot3d([(u),(1),(v)],u=-1..1, v=0..3-u^2,axes=normal):
> A6:=plot3d([(u),(-1),(v)],u=-1..1, v=0..3-u^2,axes=normal):
> display({A1,A2,A3,A4,A5,A6}, labels=[x,y,z],scaling=constrained, view = [-1.5 .. 1.5, -1.5 .. 1.5, 0 .. 4.5]);
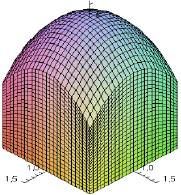
Так как основанием бруса служит квадрат со сторонами, параллельными координатным осям Ox и Oy, то пределы интегрирования по обеим переменным постоянны. Используя формулу
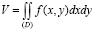 ,
,
получим:
V = 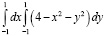 =
=
= 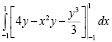 =
=
=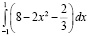 =
= 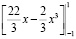 =
=
= 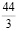 –
– 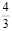 = 13
= 13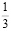 .
.
Вычисление интеграла в Maple выглядит следующим образом:
> with(student):
> Doubleint(4-x^2-y^2, y=-1..1, x=-1..1);
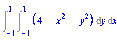
> value(%);
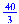
Пример 3. Вычислить площадь части поверхности 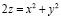 , вырезанной цилиндром
, вырезанной цилиндром 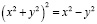 .
.
Решение. Контуром проекции вырезанной части на плоскость Оху является лемниската 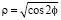 .
.
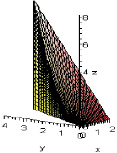
Построим общий вид пересекающихся поверхностей:
> with(plots):
> with(student):
> A1:=plot3d([(u),(v),((u^2+v^2)/2)], u=-4..4,v=-4..4,axes=normal):
> A2:=plot3d([(u),((1/2)*sqrt(-2-4*u^2+2*sqrt(8*u^2+1))),(v)], u=-1..1,v=-1..1,axes=normal):
> A3:=plot3d([(u),(-(1/2)*sqrt(-2-4*u^2+2*sqrt(8*u^2+1))),(v)],u=-1..1, v=-1..1,axes=normal):
> display({A1,A2,A3,A4,A5},labels=[x,y,z],scaling=constrained,view = [-1.5 .. 1.5, -1.5 .. 1.5, 0 .. 1]);
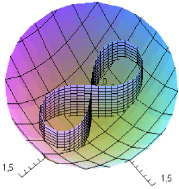
Построим вырезаемую цилиндром поверхность:
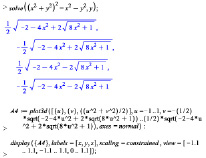
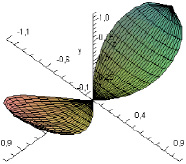
Цилиндр вырезает из параболоида два равных куска поверхности. Из уравнения параболоида
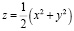
получим подынтегральную функцию, для которой
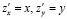 ,
,
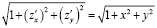 .
.
Следовательно,
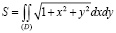 .
.
Преобразуем интеграл к полярным координатам 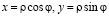 . Подынтегральная функция запишется в виде
. Подынтегральная функция запишется в виде
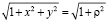 ,
,
а уравнение лемнискаты – в виде
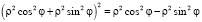 ,
,
или 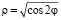 . Так как параболоид и цилиндр симметричны относительно плоскостей Охz, Oyz, то достаточно вычислить интеграл по одной четвертой части лемнискаты, расположенной в первой четверти плоскости Oxz:
. Так как параболоид и цилиндр симметричны относительно плоскостей Охz, Oyz, то достаточно вычислить интеграл по одной четвертой части лемнискаты, расположенной в первой четверти плоскости Oxz:
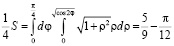 ,
,
откуда
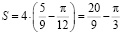 .
.
Вычисление интеграла в Maple:
> with(student):Doubleint(4*rho*sqrt(1+rho^2), rho=0..sqrt(cos(2*phi)), phi=0..Pi/4);
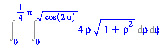
> value(%);
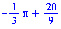
Заключение
Применение в учебном процессе не только «ручных», но и компьютерных вычислений делает процесс математического моделирования ситуации более наглядным и представимым для обучающихся (особенно в случае трёхмерного пространства); позволяет уменьшить трудоёмкость выкладок (что особенно важно при изучении курса высшей математики на непрофильных направлениях подготовки) и сравнить математический и компьютерный методы решения одной и той же математической проблемы (что полезно для студентов профильного уровня обучения).
Библиографическая ссылка
Шерстнева Н.А. ИСПОЛЬЗОВАНИЕ СИСТЕМЫ КОМПЬЮТЕРНОЙ МАТЕМАТИКИ MAPLE В УЧЕБНОМ ПРОЦЕССЕ // Международный журнал экспериментального образования. 2015. № 11-2. С. 231-234;URL: https://expeducation.ru/ru/article/view?id=8382 (дата обращения: 17.11.2025).

