Сегодня во всех сферах человеческой деятельности востребованы специалисты, обладающие не просто системой предметных знаний, а интеллектуально развитые личности, умеющие самостоятельно принимать ответственные решения в ситуации множественности выбора, способные находить инновационные решения в условиях неопределенности.
Все это требует развития такого важного интеллектуального качества как гибкость мышления. Гибкость мышления учащийся проявляет тогда, когда он [4]:
– предлагает несколько способов использования предмета, отличающихся от обычного;
– выражает много мыслей, идей или проблем;
– может перенести смысловое значение одного объекта на другой объект;
– легко может поменять один фокус зрения (подхода) на возможный другой;
– выдвигает множество идей и исследует их;
– думает о различных путях решения проблемы.
Гибкость мышления есть компонент креативного мышления.
Дж. Гилфорд с сотрудниками гипотетически выделили шестнадцать интеллектуальных способностей, характеризующих креативность. Среди них: семантическая гибкость (способность выявить основное свойство объекта и предложить новый способ его использования); образная адаптивная гибкость (способность изменить форму стимула таким образом, чтобы увидеть в нём новые признаки и возможности его использования); семантическая спонтанная гибкость (способность продуцировать разнообразные идеи в нерегламентированной ситуации).
Позже Дж. Гилфорд остановился на шести параметрах креативности (дивергентное мышление): способность к обнаружению и постановке проблем; «беглость мысли» (количество идей, возникающих в единицу времени); оригинальность (способность производить идеи, отличающиеся от общепринятых взглядов, отвечать на раздражители нестандартно); гибкость – способность продуцировать разнообразные идеи; способность решать проблемы, то есть к анализу и синтезу; способность усовершенствовать объект, добавляя детали.
Более подробный разговор о креативности мышления учащихся и о средствах его развития читатель найдет в нашей работе [3].
Дж. Гилфорд рассматривал креативность как общую творческую способность. И коль скоро гибкость мышления есть составляющая креативности, то ясно, что развивая гибкость мышления, мы развиваем творческое мышление.
К средствам развития гибкости мышления можно отнести: отказ в обучении от шаблона, стереотипа; решение задач различными методами и способами; доказательство теорем различными методами и способами и т. д.
Практика, а так же результаты научных исследований [1,2] показывают, что средством развития гибкости мышления так же является работа, связанная с обращением математической задачи.
Следуя О.М. Абрамовой [1], мы под обращением математической задачи будем понимать последовательное видоизменение ее путем извлечения из условия части или даже всех данных и включение их в требование задачи; при этом из него, соответственно, исключаются несколько или все найденные искомые и переводятся условие.
Обращенная задача станет обратной по отношению к исходной, если все ее требования и условия полностью поменяются местами.
Вводят специальную характеристику – меру обращенности задачи. Дадим пояснение.
Обозначим число элементов условия исходной задачи через Yк, а число искомых в ее требовании через Тm, число данных, перешедших после процесса обращения задачи в ее требования, примем за 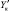 , а число искомых, включенных в ее условие, – за
, а число искомых, включенных в ее условие, – за 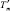 . Тогда, обозначив меру обращенности задачи через n, будем иметь формулу:
. Тогда, обозначив меру обращенности задачи через n, будем иметь формулу:
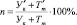
Если, например, в условии задачи содержится четыре элемента, а в требованиях задачи – два элемента, то потенциал обращения этой задачи будет считаться по формуле: Р = (2n – 1)(2k – 1), где n – число данных задачи; k – число ее искомых. В данном случае имеем Р = (24 – 1)(22 – 1) = 15∙3 = 45. То есть в результате обращения исходной задачи, возможно получить 45 обращенных задач (конечно, не все обращенные задачи получаются корректно поставленными).
Задача 1. Из населенного пункта А выехал велосипедист со скоростью 20 км/ч, а из пункта В навстречу ему в то же время выехал другой велосипедист со скорость 25 км/ч. Найти время их движения до места встречи, если расстояние АВ равно 135 км.
Решение
1) 20 + 25 = 45 км/ч – скорость сближения;
2) 135:45 = 3 ч – время встречи велосипедистов.
Приведем обращенные задачи к исходной задаче.
Задача 1.1
Из двух населенных пунктов А и В одновременно выехали навстречу друг другу велосипедисты. Скорость велосипедиста, вышедшего из пункта А, равна 20 км/ч. Найти скорость велосипедиста, вышедшего из пункта В, если велосипедисты встретились через 3 ч, а путь АВ равен 135 км.
Решение
1) 20∙3 = 60 км – путь, пройденный велосипедистом, вышедшим из пункта А, до места встречи;
2) 135 – 60 = 75 км – путь, пройденный вторым велосипедистом до места встречи;
3) 75:3 = 25 км/ч – скорость велосипедиста, вышедшего из пункта В.
Задача 1.2
Из двух населенных пунктов А и В одновременно выехали навстречу друг другу велосипедисты. Скорость велосипедиста, вышедшего из пункта В, равна 25 км/ч. Найти скорость велосипедиста, вышедшего из пункта А, если велосипедисты встретились через 3 ч, а путь АВ равен 135 км.
Решение
1) 25∙3 = 75 км – путь, пройденный велосипедистом, вышедшим из пункта В, до места встречи;
2) 135 – 75 = 60 км – путь, пройденный вторым велосипедистом до места встречи;
3) 60:3 = 20 км/ч – скорость велосипедиста, вышедшего из пункта А.
Задача 1.3
Из населенного пункта А выехал велосипедист со скоростью 20 км/ч, а из населенного пункта В в то же время навстречу ему выехал другой велосипедист, со скорость 25 км/ч. Найти расстояние АВ, если велосипедисты встретились через 3 ч.
Решение
1) 20∙3 = 60 км – путь, пройденный велосипедистом, вышедшим из пункта А, до места встречи;
2) 135 – 60 = 75 км – путь, пройденный вторым велосипедистом до места встречи;
3) 60 + 75 = 135 км – длина пути АВ.
Конечно, вначале должен сам учитель показывать, как составляются обращенные задачи, а уже затем предлагать учащимся выполнять это действие самостоятельно.
Библиографическая ссылка
Далингер В.А. РАБОТА ПО ОБРАЩЕНИЮ МАТЕМАТИЧЕСКИХ ЗАДАЧ КАК СРЕДСТВО РАЗВИТИЯ ГИБКОСТИ МЫШЛЕНИЯ УЧАЩИХСЯ // Международный журнал экспериментального образования. 2015. № 12-1. С. 18-19;URL: https://expeducation.ru/ru/article/view?id=8669 (дата обращения: 14.01.2026).

