При перемещении частицы по горизонтальной поверхности или по кривой линии, связи кинематических параметров установлены только в самой общей математической форме и в силу этого не нашли применения для инженерных расчетов перемещения частиц с рабочим органов в виде винтовой поверхности. Рассмотрим случай когда имеется транспортер с рабочим органом в виде винтовой поверхности и с образующими, перпендикулярными к оси рабочего органа. При этом будем считать, что образующая рабочего органа неподвижна, а винтовая поверхность вращается вокруг своей оси с постоянной угловой скоростью w.
Приложенными к частице силами будут: G=mg – сила тяжести, Н; N2 – нормальная реакция поверхности кольца, Н; N1 – нормальная реакция элемента винтовой поверхности, Н; f2N2 – сила трения частицы о поверхность кольца, Н; f1N1 – сила трения частицы о элемент винтовой поверхности, Н.
Направление сил за исключением силы трения частицы о поверхность кольца являются заданными. Причем вследствие того, что образующие винтовой поверхности перпендикулярны к его оси, реакция N1 и сила трения f1N1 во всех точках движения будут лежать в плоскостях, показанных на рисунке 2.
Для определения направления силы трения f2N2 необходимо знать положение касательной к траектории движения частицы по поверхности кольца рабочего органа, поскольку она направлена по этой касательной в сторону, обратную направлению скорости ее движения. Следовательно, направление данной силы трения будет меняться с изменением направления скорости движения частицы [1, 2]. Отнесем движущуюся частицу материала к осям координат x,z, приняв левую систему отсчета. Тогда дифференциальные уравнения движения частицы в проекциях на оси координат можно написать так (при условии, что N2>0 ). Приняв теперь во внимание, что 
, и подставив в уравнение значения и получим:
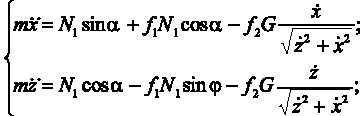(1)
где m – масса частицы, кг; 
– вторая производная от перемещения по оси x, м/с2; f1 – коэффициент трения частицы о элемент винтовой поверхности; a=const – угол наклона винтовой линии рабочего органа к плоскости поперечного сечения винтовой поверхности, град; f2 – коэффициент трения частицы о поверхность кольца; 
– первая производная от перемещения по оси x, м/с; 
– первая производная от перемещения по оси z, м/с; 
– вторая производная от перемещения по оси z, м/с2.
Библиографическая ссылка
Исаев Ю.М., Семашкин Н.М., Злобин В.А., Вечкуткин А.В. ДВИЖЕНИЕ ЧАСТИЦЫ МАТЕРИАЛА ПО ОБРАЗУЮЩЕЙ СПИРАЛЬНОГО ВИНТА // Международный журнал экспериментального образования. – 2015. – № 12-3. – С. 422-422;URL: https://expeducation.ru/ru/article/view?id=9151 (дата обращения: 22.12.2024).