При изучении любого раздела физики каждый преподаватель несомненно должен начать свою лекцию с того, что представляет собой этот раздел физики, границы его применимости, область действия, основные закономерности, взаимосвязь с другим разделом физики и т.д. Например классическая физики и релятивистская физика, чем они отличаются, какие законы действуют в том или другом разделе физики. Самое главное между этими разделами имеется такая область, когда скорости тел малы, тогда справедливы преобразования Г. Галилея при переходе от одной инерциальной системы отсчета к другой, когда скорости тел близки к скоростям света в вакууме, тогда справедливы преобразования Лоренца. В предельном случае, когда мы рассматриваем маленькие скорости, тогда преобразования Лоренца автоматически переходят к преобразованиям Галилея.
Вот такая взаимная связь разных разделов физики показывает справедливость обоих преобразований, эту область перехода одних законов в другую область называют квазиклассическим приближением. Такое квазиклассическое приближение можно привести также для квантовой механики и классической механики, для других разделов тоже можно показать аналогичный переход. Это квазиклассическое приближение показывает именно ту область границы перехода разных разделов физики.
Рассмотрение взаимосвязи разных разделов физики, также изучение условий переходов между этими разделами физики небходимо для многих учащихся и студентов. Во-первых, у обучающегося складывается конкретное представление например про курс квантовой механики и классической механики, также про их взаимосвязь, условий переходов между этими разделами физики.
Многим известно, что в последние годы проводились исследования на Большом Адронном Коллайдере, эти эксперименты скоро будут продолжены. Мы не будем подробно рассказывать об этих исследованиях, о задачах исследования, о проблемах с Большим Адронным Коллайдером и т.д., отметим только то, что одной из главных задач этих исследований является подтверждение Стандартной Модели в физике. Что означает Стандартная Модель?
В физике мы знаем что существуют четыре типа взаимодействий в природе, это сильное, слабое, электромагнитное, гравитационное взаимодействие. Сильное, слабое, электромагнитное взаимодействие объединяют в одну группу, так называемую Стандартную Модель. Именно подтверждение справедливости законов Стандартной Модели должны получить на Большом Адронном Коллайдере. Возможно и Стандартная Модель будет частично подтверждена, но будет как-то дополнена, появится определенный круг вопросов для физиков-теоретиков, для экспериментаторов,могут проявляться и некоторые свойства 4-мерного, N-мерного пространства и т.д.
Резюмируя можно сказать, что любая новая теория в предельном случае должна подтвердить справедливость старой теории, вот такой переход существует между квантовой и классической механикой, т.е. имеется между ними предельный переход – квазиклассическое приближение.
Известно, что теория квантовой механики в предельном случае всегда должна переходить в формулы классической механики, так как любая новая теория должна иметь общую граничную область со старой теорией. Например преобразования Лоренца в специальной теории относительности А. Эйнштейна в предельном случае когда скорости тел малы по сравнению со скоростью света в вакууме 
переходят в преобразования Г. Галилея.
Аналогично свету который имеет двойственную корпускулярно-волновую природу, также любая частица имеет такую же двойственную природу. Экспериментально доказано, что от любой частицы (например электрон, протон, нейтрон и т.д.) мы можем наблюдать дифракционную картину на экране. Исходя из этого, из многочисленных опытов по дифракции света от отдельных частиц Де-Бройль получил свою формулу которая связывает длину волны и импульс частицы 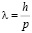[1].
. (1)
Данная формула показывает взаимосвязь корпускулярной и волновой природы любой частицы (р и l). Отсюда вытекает что частицы как и свет показывают характеристики корпускулы и волны. Всем известно, что свет имеет двойственную природу, в одних случаях он ведет себя как волна например явления дифракций света, интерференций света, поляризаций света, дисперсии света, в других явлениях свет ведет себя как корпускула, поток частиц это такие явления, как фотоэффект, эффект комптона, фотоны и другие явления. <
Нужно отметить, что имеются такие явления, где наблюдаются и волновые, и копускулярные свойства света, это проявляется например в опыте по определению давления света. По аналогии со светом у многих крупных ученых в начале двадцатого века возник такой вопрос возможно и элементарные частицы тоже имеют также двойственную природу. В таком случае и элементарным частицам должна быть присуща и корпускулярная природа, и волновая природа, по аналогии со светом- электромагнитной волной и потоком частиц. Здесь естественно возникает следующий вопрос: как в данном случае мы можем рассматривать электрон, это частица или волна?
В квантовой механике на этот вопрос есть конкретный ответ: электрон –это микрочастица, со специфическими свойствами, иногда она проявляет свои волновые свойства, иногда она проявляет свои корпускулярные свойства. Для обьяснения взаимосвязи между теориями квантовой механики и классической механики рассмотрим собственные значения энергии в бесконечно глубокой потенциальной яме, также выясним ее взаимосвязь с энергией в классическом случае. Энергия микрочастицы в бесконечно глубокой потенциальной яме определяется следующим выражением:
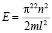. (2)
Данная формула показывает что собственные значения энергии принимают дискретные значения, они зависят от главного числа п. Значит значения энергии микрочастицы в глубокой потенциальной яме оказываются квантованными. Действительно формула (2) удовлетворяют принципу неопределенности Гейзенберга.
В справедливости и выполнения формулы (2) только для квантовой механики можно наглядно убедиться. Например если в данной формуле например масса микрочастицы будет много больше массы электрона, или ширина потенциальной ямы l будет больше размеров атома или ядра, или когда n стремится к бесконечности тогда данная формула автоматически теряет смысл.
Если главное квантовое число будет очень большое, тогда дискретность квантовых состояний перестает проявляться, при этом фактически происходит переход к непрерывному изменению энергии.
Эта формула определяет собственные значения энергии микрочастицы в потенциальной яме, она пригодна только для квантовой механики, т.е. явлений происходящих в микромире. Аналогично и квадрат волновой функции когда главное квантовое число стремится к бесконечности из квантомеханического распределения переходит в классическое распределение [1-3].
В квантовой механике есть такое понятие «заданное состояние системы». Состояние системы задано, если задана волновая функция, описывающая эту систему. Однако,мы ни при какихусловиях не можем непосредственно измерить саму волновую функцию. Физический смысл имеет лишь квадрат модуля ее, трактуемый, как соответствующая вероятность. Выход из этого кажущегося противоречия заключается в следующем:когда мы говорим, что задано состояние системы, то это означает, что задано значение определенной совокупности квантомеханических величин.Эта совокупность величин, задание которой полностью определяет состояние системы, называется полным набором квантомеханических величин.
В классической физике, чтобы задать состояние системы в какой-то момент времени, нам требовалось задать значения всех обобщенных импульсов и обобщенных координат в этот момент времени. Если классическая система имеет S степеней свободы, тогда требуется задать значения 2S переменных величин [4,5].
Теперь рассмотрим квазиклассическое приближение квантовой механики. Нужно отметить следующее обстоятельство, что при решении уравнения Шредингера мы не можем представить постоянную Планка равным нулю, так как в этом случае данное уравнение теряет смысл.
Поэтому мы волновую функцию представим через экспоненциальную функцию выраженную от функции S, разложим ее формально в ряд по степеням. Если дебройлевские длины волн частиц малы по сравнению с характеристическими размерами L, определяющими условия данной конкретной задачи, то свойства системы близки классическим. (По аналогии с тем, как волновая оптика переходит в геометрическую при стремлении длины волны к нулю) [1-3].
Рассмотрим движение микрочастицы по оси ох, тогда при решении уравнения Шредингера мы получаем для микрочастицы механическое действие S, которое определяется следующим выражением:
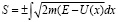. (3)
Эта формула представляет собой не что иное, как классический импульс частицы р(х), зависящий от координаты ох. Значит импульс частицы определяется следующим выражением:
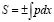; (4)
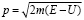, (5)
что соответствует классическому определению импульса. В данном случае, мы опускаем многие теоретические преобразования, так как хотим отдельно отметить именно предельный случай, когда формулы квантовой механики переходят в формулы классической механики.
Такой переход квазиклассического приближения выполняется тогда, когда мы при разложении механического действие S, берем только начальные два члена разложения этой функции. Одним словом условие квазиклассического приближения записывается следующим образом:
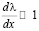. (6)
Отсюда можно сделать следующий главный вывод: для выполнения условия квазиклассичности длина волны микрочастицы( волны де Бройля) должна мало меняться на протяжении расстояний сравнимой с ее размерами. Ну а где это условие не выполняется, тогда квазиклассическое приближение в этих областях становится неприменимым.
Следующий главный вывод заключается в том, что при достаточно медленном изменении потенциальной энергии от точки к точке, когда на длине волны порядка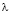 
не происходит заметного изменения импульса частицы справедливо выполняется квазиклассическое приближение [3,4].
Если импульс частицы становится мала, тогда квазиклассическое приближение становится непригодным. Например это приближение неприменимо вблизи точек поворота, тогда вблизи этих точек по законам классической механики, частица остановилась бы, и стала бы двигаться в обратном направлении. Эти точки поворота соответствуют случаю, когда
,
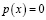импульс равен нулю, значит,
Е=U(х).
Когда импульс стремится к нулю
,
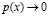де-Бройлевская длина волны стремится к бесконечности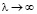 
[3,4].
Библиографическая ссылка
Абекова Ж.А., Оралбаев А.Б., Айдарбеков Н., Баубекова М.К. МЕТОДОЛОГИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ПРИ РАССМОТРЕНИИ ОСНОВНЫХ ВОПРОСОВ МИКРОМИРА // Международный журнал экспериментального образования. – 2016. – № 4-1. – С. 12-15;URL: https://expeducation.ru/ru/article/view?id=9729 (дата обращения: 21.12.2024).