Одной из наиболее важных задач, возникающих в различных областях человеческой деятельности (технической, экономической, организационной и др.) является проблема распределения и перераспределения ресурсов, причем оптимальным образом [1,2].
Данная работа посвящена распределению ресурсов, когда выполняемые работы являются взаимосвязанными.
Рассмотрим комплекс взаимосвязанных работ, состоящий из m узлов показанный на рисунке 1.
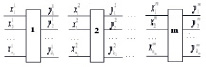
Рисунок 1. Комплекс взаимосвязанных работ
Выходы каждого узла распределяются между входами последующего узла. Входы первого узла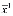 
=(
,
,...,
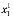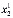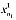), второго узла 
=(
,
,...,
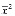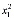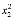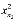) и т.д. m- го узла 
=(
,
,...,
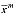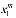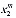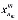). Выходы узлов определяются переменными 
=(
,
,…,
), 
=(
,
,…,
), . . ., 
=(
,
,…,
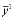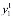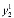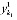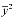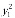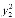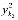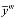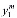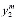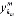), соответственно.
Предположим, что выход каждого i- го узла зависит от входа i- го узла линейно, а именно
=
, 
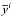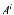
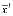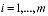, (1)
где
=
, 
.
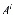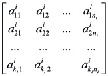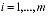Допустим также, что выходы каждого i- го узла линейно распределяются между входами i+1- го узла, то есть
=
, 
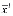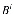
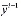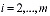, (2)
где
=
, 
.
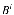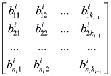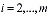Тогда воспользуюсь (1) и (2) для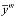 
имеем
=
=
=
=
=
…
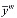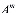
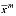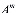
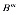
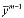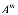
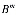
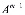
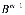
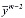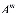
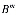
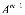
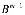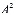
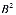
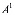
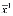. (3)
Если обозначим через A=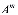
=
…
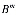
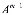
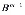
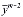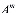
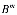
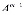
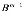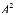
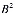
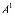, то (3) имеет вид
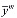= A
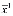. (4)
Определим теперь затраты на приобретения входного продукта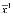 
:
=
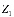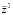
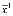, (5)
где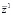 
=(
,
,...,
), 
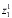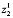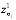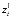-затраты на приобретения единицы 
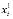-ой продукции.
Затраты на производства продукции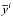 
в линейном случае определяется как
=
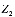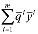, (6)
где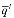 
=(
,
,...,
), 
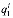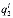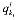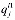-затраты на производства единицы 
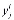-ой продукции.
Эффективность зависит от прибыли, получаемое от реализации выпуска продукции m-го узла. Поэтому необходимо максимизировать целевую функцию
L= 
-
-
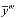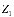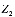, (7)
где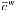 
=(
,
,...,
), 
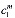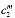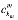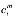-стоимость единицы 
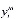-ой продукции.
Если количество ресурсов ограничено(<=R), то
+
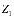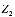= R. (8)
Задача заключается в максимизации (7) при ограничениях (4) и (8). Эта задача является задачей линейного программирования и решается симплекс методом.
Пример. Пусть комплекс взаимосвязанных работ имеем вид, как показан на рисунке 2.
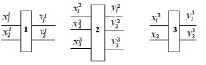
Рисунок 2. Пример взаимосвязанных работ
Исходные данные следующие:
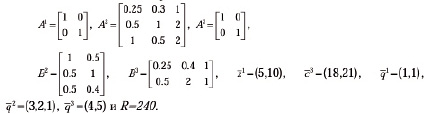
Необходимо определить максимальную прибыль.
Решение.
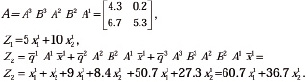
Целевая функция имеет вид
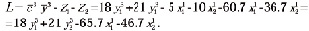
Ограничение (8) имеет вид
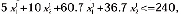
или
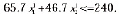
а ограничения (4) можно представить в виде
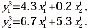
Если ввести обозначения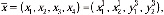 
то получим следующую задачу линейного программирования
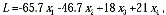при ограничениях
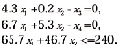
Если решить задачу симплекс методом, то получим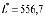 
и количества произведенной продукции 
=
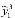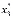=15,7 и 
=
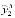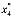=24,5.
Результаты работы могут быть использованы для оптимального распределения ресурсов в различных организациях, где имеется комплекс взаимосвязанных работ.
Библиографическая ссылка
Ташев А.А., Балабекова М.Ж. ОПТИМАЛЬНОЕ ПЛАНИРОВАНИЕ ВЫПУСКА ПРОДУКЦИИ РАСПРЕДЕЛЕНИЕ РЕСУРСОВ ДЛЯ ВЫПОЛНЕНИЯ КОМПЛЕКСА ПОСЛЕДОВАТЕЛЬНО ВЗАИМОСВЯЗАННЫХ РАБОТ (МНОГОМЕРНЫЙ СЛУЧАЙ) // Международный журнал экспериментального образования. 2014. № 8-1. С. 88-90;URL: https://expeducation.ru/ru/article/view?id=5808 (дата обращения: 01.11.2025).