Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Далингер В.А. 1

---

1 Омский государственный педагогический университет

Статья в формате PDF

0 KB

1. Далингер В.А. Методика обучения учащихся доказательству математических предложений: книга для учителя. – М.: Просвещение, 2006. – 256 с. (Библиотека учителя).

2. Итоговая аттестация выпускников начальной школы: комплексная работа / [В. Ю. Баранова, М.Ю. Демидова, Г.С. Ковалева и др.]; под ред. Ковалевой. – М.: Просвещение, 2011.

3. Метапредметные результаты. Стандартизированные материалы для промежуточной аттестации: 5 класс: Варианты 1, 2 и 3, 4. – М., СПб.: Просвещение, 2014.

4. Метапредметные результаты. Стандартизированные материалы для промежуточной аттестации: 5 класс: пособие для учителя (в комплекте с электронным приложением) / Г.С. Ковалева и др.; под ред. Г.С. Ковалевой, Е.Л. Рутковской. – М.; СПб.: Просвещение, 2014.

5. Метапредметные результаты. Стандартизированные материалы для промежуточной аттестации: 6 класс: Варианты 1, 2 и 3, 4. – М., СПб.: Просвещение, 2014.

6. Метапредметные результаты. Стандартизированные материалы для промежуточной аттестации: 6 класс: пособие для учителя (в комплекте с электронным приложением) / Г.С. Ковалева и др.; под ред. Г.С. Ковалевой, Е.Л. Рутковской. – М.; СПб.: Просвещение, 2014.

7. Метапредметные результаты: стандартизированные материалы для промежуточной аттестации: 7 класс: пособие для учителя / Г.С. Ковалева, М.Д. Демидова, Л.Ф. Иванова и др.; под ред. Г.С. Ковалевой. – М., СПб.: Просвещение, 2016. – 167 с.

8. Программа формирование универсальных учебных действий (УУД) у обучающихся на ступени начального образования. – М.: Просвещение, 2010. – 151 с.

9. Серегин Г.М. Диагностика и прогнозирование необходимого уровня понимания учащихся математического материала: монография. – Новосибирск: Изд-во НГПУ, 2008. – 220 с.

10. Сметанникова Н.Н. Стратегиальный подход к обучению чтению. – М.: Школьная библиотека, 2005.

11. Усачева И.В. Курс эффективного чтения учебного и научного текста. – М.: Изд-во МГУ, 2000.

12. Хиленко Т.П. Типовые задачи по формированию универсальных учебных действий. Работа с информацией, 4 класс: пособие для учащихся общеобразовательных организаций. – М.: Просвещение, 2014. – 96 с. (Работаем по стандартам).

13. Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов // Математика в школе. – 2006. – № 4. – С. 35 – 41.

В новых федеральных государственных образовательных стандартах (ФГОС) результаты освоения основной образовательной программы образовательного учреждения для начальной, основной, полной школы выражены в трех аспектах: личностные, предметные и метапредметные.

К метапредметным результатам обучения в новых стандартах отнесены и умение осознанного чтения, и умения работать с информацией. Учащиеся, обучаясь различным учебным предметам, должны овладеть общеучебными действиями, связанные с чтением, пониманием текстов, преобразованием текстов, а также с использованием информации из текстов для различных целей.

Задача школы – обучать думать над текстом, понимать текст, а не воспринимать лишь его; чтение – это диалог автора и читателя.

И.В. Усачева [11] указывает следующие приемы понимания учебного текста:

– прием постановки вопросов к тексту;

– прием составления плана;

– прием составления граф-схемы;

– тезирование;

– прием составления сводных таблиц;

– комментирование.

Важным компонентом метапредметных результатов является смысловое чтение. Заметим, что без этого важного метапредметного результата невозможно обеспечить формирование многих других личностных, предметных и метапредметных результатов.

Смысловое чтение, как метапредметный результат, формируется в начальной школе, а затем продолжает формироваться с 5 по 9 класс.

Конечно, работа по овладению учащимися поиском информации и пониманием прочитанного, преобразованием и интерпретацией информации, оценкой информации должна проводиться на том тексте, который имеется в учебниках алгебры и геометрии, но для этого можно использовать и дополнительный материал.

В качестве примеров приведем следующие задания.

Задание 1. Глядя на рисунок (рис. 1), ответьте, верно ли следующее утверждение?

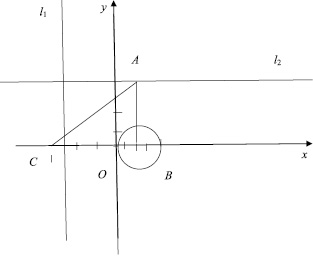
Рис. 1

1) Точка (–1;3) лежит в треугольнике АВС.

2) Точка (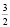; 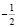) лежит в круге.

3) Точка (2;2) лежит на границе треугольника АВС.

4) Точка (0;2) находится ближе к А, чем к В.

5) Точка (1;0) находится ближе к l2 ,чем к l1.

6) Точка (0;0) образует с точками А и С остроугольный треугольник.

7) Точка (–4;1) лежит левее l1 и ниже l2.

8) Точка (1;–4) лежит правее l1 и ниже l2.

9) Точка (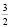; 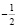)) лежит в круге и не лежит в треугольнике АВС.

10) Точка (–2; 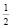) не попала в круг, но лежит в треугольнике АВС.

11) Точка (–3;1) лежит ниже l2 и не левее l1.

12) Если какая-то точка попала в круг, то она лежит ниже прямой l2.

13) Если точка лежит левее l1, то она или в третьей, или в четвертой четверти.

14) Если точка попала в треугольник АВС и в круг, то она лежит в первой четверти.

15) Если точка из второй четверти попала в треугольник АВС, то она не может попасть в круг.

Задание 2. Верно ли, что на рисунке (рис. 2):

1) есть хотя бы один белый треугольник;

2) не больше одного белого треугольника;

3) есть хотя бы два белых треугольника;

4) не больше двух кругов;

5) все четырехугольники черные;

6) среди белых фигур нет четырехугольников;

7) если фигура черная, то она – четырехугольник;

8) по крайней мере, половина фигур – белые.

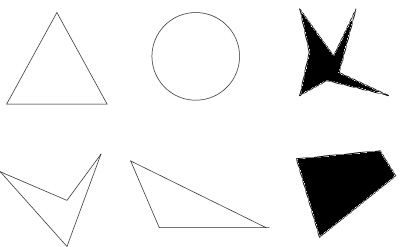
Рис. 2

Задание 3. Приведите примеры, доказывающие, что нижеперечисленные определения ошибочны:

а) прямоугольником называется четырехугольник, у которого диагонали равны;

б) прямоугольником называется четырехугольник, имеющий хотя бы два прямых угла;

в) параллелограммом называется четырехугольник, две противоположные стороны которого параллельны;

г) параллелограммом называется многоугольник, противоположные стороны которого попарно равны;

д) квадратом называется многоугольник, все стороны и все углы которого равны между собой;

е) квадратом называется такой многоугольник, у которого четыре стороны и четыре угла равны между собой.

Задание 4. Дан русский текст и его перевод (построчный) на языке Ам-Ям (табл. 1).

Таблица 1

Составьте фрагмент русско-ам-ямского словаря по этому переводу. В языке Ам-Ям нет знаков препинания.

Решение

1) Слова: «гулять», «видеть», «поймать» встречаются в своих строчках по одному разу, поэтому им соответствуют слова: «му», «бу», «гу».

2) Так как слово «мышь» встречается во всех трех сточках, то ему соответствует «ту».

3) Так как слово «ночь» встречается в первой и во второй строчках, то ему соответствуют «ам».

4) Так как слово «пошла» встречается в первой и третьей строчках, то ему соответствует «ям».

5) Так как слово «кошка» встречается во второй и третьей строчках, то ему соответствует «ля».

Ответ: фрагмент словаря выглядит так: гулять – му, видит – бу, поймать – гу, мышь – ту, ночью – ам, пошла – ям, кошка – ля.

Задание 4. Поменяйте местоположение только одной карточки (рис. 3), чтобы получить верное равенство.

Рис. 3

Ответ: рис. 4.

Рис. 4

Предложенные задания направлены на проверку умения сопоставлять вербальную и графическую информацию, по ходу чтения текста анализировать рисунки.

В нашей работе [1] читатель найдет и другой материал, относящийся к формированию у учащихся умения работать с чертежом, графической информацией и другими аспектами смыслового чтения и работы с информацией.

Приведем таблицу (табл. 2), в которой соотнесем различные вопросы и мыслительные операции, активизируемые этими вопросам (по Д. Халперну) [10, с. 129].

Таблица 2

Одной из основных проблем, возникающих при обучении, является проблема понимания математического текста, и, в частности, текста математической задачи.

Этой проблеме в научно-методической литературе уделено достаточно много внимания (Э.К. Брейтигам, Л.П. Доблаев, Я.А. Микк, А.И. Новиков, Г.М. Серегин, Г.Д. Чистякова и др.).

М. В. Шнейдерман [13], анализируя работы более 4000 учащихся 5 классов, ошибки и затруднения, вызванные неправильным пониманием условия задачи, составляют 18% всех ошибок, а установление неправильных связей между данными задачи – 14 % .

Осознанному построению учащимися процесса усвоения математического материала способствует рефлексивная деятельность.

Способом, позволяющим добиться лучшего понимания учебного текста, является постановка вопросов и нахождение на них ответов. Причем возможны три способа задавания вопросов:

– учитель задает ученику вопросы после прочтения учебного текста, а он отвечает на них;

– учитель, перед прочтением учеником учебного текста, ставит предварительные вопросы, а он ищет на них ответы в процессе чтения;

– ученик сам ставит себе вопросы по ходу чтения и пытается на них ответы.

Вопрос – это выраженная в вопросительном предложении мысль, направленная на уточнение или дополнение знаний.

Познавательная функция вопроса реализуется в форме ответа на поставленный вопрос. Ответ – это новое суждение, уточняющее или дополняющее в соответствии с поставленным вопросом прежнее знание.

На неполноту или неопределенность знания, содержащегося в вопросе, указывают операторы вопроса, то есть вопросительные слова: «Кто?», «Что?», «Когда?», «Почему?» и др.

По познавательной функции вопросы подразделяются на два основных вида: уточняющие и восполняющие [9].

Уточняющим (определенным, прямым или ли-вопросом) является вопрос, направленный на выявление истинности выраженного в нем суждения. Например: «Бывают ли треугольники с двумя прямыми углами»; «Действительно ли, что квадрат – это ромб?».

Уточняющие вопросы делятся на условные и безусловные. Например: «Верно ли, что гипотенуза больше катета?» – простой безусловный вопрос. «Верно ли, что если две прямые на плоскости перпендикулярны третьей, то они параллельны?» – простой условный вопрос.

Восполняющие вопросы («Что – вопросы») – это выбор истинного суждения из множества возможных. Например: «К какому виду относится треугольник со сторонами 2 см, 5 см и 3 см: а) остроугольный, б) тупоугольный, в) такого треугольника не существует, г) прямоугольный?».

Отметим, что постановка вопроса есть прием лучшего понимания текста.

Библиографическая ссылка