Чрезвычайные ситуации техногенного характера – далеко не редкое явление в нашей жизни. Особенно опасны разливы и выбросы в воздух агрессивных жидкостей и газовых смесей (ОВ). В подобных ситуациях требуется достаточно много сил и средств для проведения аварийно-спасательных работ (АСР). Главный же критерий – время начала АСР.
Действия спасателей должны быть хорошо спланированными, то есть в первую очередь надо знать зависимость между объемом агрессивной жидкости или газа и теми метеоусловиями, в которых произошла авария. Это соотношение определяет глубину проникновения агрессивных сред на территорию населенного пункта. И часто такую закономерность при осуществлении обучения студентов в вузах и профессиональных спасателей на курсах повышении квалификации преподаватели учебных заведений устанавливают стереотипно, по табличным данным, в силу того, что машинные варианты требуют хорошего владения компьютером. Тем не менее, ряд статистических софтов, напрямую не используемых при расчетах, связанных с ЧС, достаточно просты в применении, и могут оказать ощутимую помощь в прогнозировании.
Мы предлагаем, при обучении приемам прогнозирования ЧС, использовать кусочно-линейную регрессию из американской программы Statistica v.6. Достоинство этого статистического модуля в том, что он не требует глубоких знаний программного обеспечения. И позволяет с первых же шагов неискушенному в тонкостях программирования пользователю легко рассчитывать регрессию именно в тех условиях, когда достижение одного критического уровня концентрации опасного для человека вещества резко меняется и, следовательно, за этими изменениями должны следовать и модели расчетов объема и времени АСР.
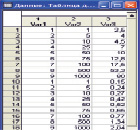
Рис. 1. Связь объемов выброса ОВ и глубины его распространения
Для подтверждения своих слов, приводим эмпирические данные, получения регрессии объема выбросов в окружающую среду сернистого ангидрида, и глубины распространения этого ОВ на открытой местности при скорости ветра 1 м/сек. И при двух диаметрально противоположных метеоусловиях: инверсии и конвекции. В первом случае агрессивное вещество легко распространяется по территории, во втором – достаточно трудно.
Формируем в стартовом окне программы Statistica v.6 рис. 1. В ней сосредотачиваем данные об объемах вещества в тоннах (Var 2) и глубине его проникновения в км (Var3). Видно, что в первых девяти строках (при инверсии) очень быстро с ростом объема выброса вредного вещества растет и глубина его проникновения, что, вполне естественно, требует чрезвычайно активных спасательных работ. Во втором случае, вроде бы, – все не столь трагично.
После того, как сформирована таблица, вызываем модуль нелинейное оценивание (рис. 2) и выбираем в нем – кусочно-линейная регрессия (рис. 3). В следующем окне определяем зависимые и независимые переменные и, нажав кнопку ОК, получаем прогноз (рис. 4). Полученный на основе данных рис. 4, 5, подтверждает, что тенденция распространения вредного вещества сохраняется и в первом, и во втором варианте, хотя (при конвекции) с несколько сниженной активностью.
Рис. 2. Нелинейное оценивание
Рис. 3. Кусочно-линейная регрессия
Таким образом, получены две кривых распределения: до и после точки разрыва (точка 9 на оси Х). На последнем этапе прогноза получаем регрессионные модели (рис. 6), связывающие объемы выброса с глубиной распространения вредоносного агента по территории.
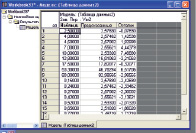
Рис. 4. Оценка совпадений эмпирических и прогнозируемых значений
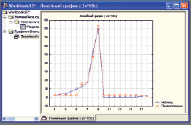Рис. 5. Прогноз распространения отравляющего вещества
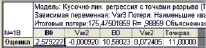
Рис. 6. Базис для расчета регрессионных уравнений
Резюмируя сказанное, хотим заметить, что в любом случае: при метеоусловиях, способствующих (и даже не способствующих) распространению химического вещества по территории, оперативная активность сотрудников аварийно-спасательных служб при ликвидации чрезвычайной ситуации, аналогичной описанной, не должна снижаться.