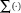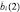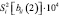Scientific journal

International Journal of Experimental Education

ISSN 2618–7159

ИФ РИНЦ = 0,425

В последнее время согласно литературным данным травма шейного отдела позвоночника у новорожденных занимает лидирующее место среди натальной травмы новорождённого. Согласно имеющиеся информации из каждых 3-х родившихся двое новорожденных получают травму шейного сегмента позвоночника при родах [1].

Травматическое разрушение анатомических структур шейного отдела позвоночника у новорожденного в процессе родов является результатом воздействия изгоняющих сил роженицы и дополнительных не всегда обоснованных медицинских пособий [2].

Основные механизмы повреждения шейного сегмента позвоночника следующие: компрессионный; дистракционный; ротационный; комбинированный.

В результате систематизации жалоб, анамнеза заболевания, объективного осмотра было собрано 52 фактора, имеющих отношение к данному заболеванию. Данные факторы представлены в табл. 1.

Таблица 1

Таблица исходных факторов

Была поставлена задача выяснить наиболее важные факторы, определяющие прогноз последствий натальной травмы позвоночника.

Алгоритм решения поставленной задачи:

– исследование таблиц исходных экспериментальных данных и мер тесноты линейных связей между факторами;

– построение, анализ корреляционных матриц, расщепление факторов на плеяды;

– применение экспертных методов – прямого ранжирования и весовых коэффициентов важности;

– построение таблицы слабокоррелированных факторов;

В представленной работе столбцами матрицы являются факторы – жалобы, анамнез заболевания, данные объективного осмотра и дополнительные инструментальные методы исследования, а строки – дети, с их реальными фамилиями и именами. Исходные данные включали в себя 52 фактора. Одним из способов понижения размерности факторного пространства из-за сокращения сильно коррелированных факторов являются корреляционные плеяды, основанные на анализе корреляционной матрицы [3].

Для выделения главных зависимостей в корреляционной матрице использовали метод корреляционных плеяд. Анализ корреляционных плеяд показал незначимость 4 факторов, в результате для дальнейшего изучения осталось 49 факторов.

Для выбора одного фактора из плеяды нами был использован экспертный метод с учетом мнения специалистов. Метод весовых коэффициентов важности (ВКВ) более удобен для эксперта с психологической точки зрения [4]. В нашей работе мы использовали метод весовых коэффициентов важности.

Эксперты заполняли верхнюю треугольную часть матрицы, на диагонали которой стоят единицы, а нижнюю треугольную часть матрицы заполнил исследователь, с последующим математическим анализом.

Таблица 2

Экспертная матрица (пример заполнения)

Таблица 3

Сводная таблица весовых коэффициентов важности второго порядка (пример заполнения)

Выводами, сделанными экспертным методом, мы доказали значимость коэффициента конкордации (согласия экспертов). Все эксперты дали не противоречивые ответы. Результаты обработки остальных анкет были сведены в табл. 3 весовых коэффициентов важности второго порядка.

Критерием, оценивающий объективность ранжировки, полученной в результате экспертизы, стал закон Г. Ципфа, который по своей сути является информационным законом самой общей природы.

Проведённый математический анализ позволил сократить размерность факторного пространства с первоначальных 49 до 4 единиц без изменения информационной емкости.

Таблица 4

Таблица факторов, имеющие наибольшее влияние на тяжесть заболевания

Выводы

1. В результате произведенных вычислений нами установлены 4 фактора, которые содержат наибольшую информационную нагрузку при натальной травме шейного отдела позвоночника

2. На базе этих четырёх факторов планируется построить вероятностную модель прогноза последствий натальной травмы позвоночника.