Возможности формирования структурированного пространства путем разбиения его на модулярные ячейки и моделирования невырожденных модулярных структур проанализированы в [9, 10]. Некоторые из этих структур с кристаллической, фрактальной и наноразмерной компонентами в 2D пространствах в [1 – 5, 7, 8, 11, 16] рассматривались как возможные абстракции сайз-распределения фаз и конфигурации межфазных границ на поверхности композиционных материалов. Сформулированы принципы их формирования, определены размерные характеристики возможных многокомпонентных структурных состояний систем [6, 12, 17]. В [7] для описания комплексного структурного состояния поверхности композиционного материала предложено учитывать состояния классов (r r), (n n) и некоторые фрактальные компоненты класса (f f). Однако, при этом не учитывалось возможное влияние состояний внутренних слоев материала на комплексное состояние поверхности композита, в частности, на условный размерный параметр поверхности, что является целью данной работы. Для достижения этой цели необходимо решить следующие задачи:
1) описание всех структурных состояний поверхности, указанных в 10–мерном гиперпространственном представлении и определение размерного параметра <D> поверхности,
2) определение влияния дополнительных по отношению к поверхности возможных компонент объемных структурных состояний на размерный параметр <D> поверхности.
Проанализируем некоторые особенности гиперпространственного представления структурных состояний поверхности материалов и методику определения размерного параметра для поверхности с учетом возможных состояний в объеме этого же материала.
Гиперпространственное представление поверхностных структурных состояний
В общем случае методика гиперпространственного представления возможных структурных состояний (10–мерной на поверхности [(r r), (n n), (f f)2D conf, (f f)*size, ((r r)f + (n n)f)site] и 15–мерной в объеме материала [(r r r), (n n n), (f f f)3D conf, (f f f)*size, ((r r r)f + (n n n)f)site] включает в себя следующие процедуры:
– описание структурных состояний из кристаллической ((r r) и (r r r)) и наноразмерной ((n n) и (n n n)) компонент композита,
– описание вероятных квазифрактальных конфигураций межфазных границ (f f)2Dconf и (f f f)3Dconf, которые являются 2D и 3D оболочками системы элементов детерминистических модулярных структур с соответствующими фрактальными состояниями,
– описание вероятных квазифрактальных 1D, 2D или 3D распределений элементов по позициям детерминистических модулярных структур (описания site-распределений
(f f)site = (f f)*) и (f f f)site = =(f f f)*),
– описание вероятных квазифрактальных 1D, 2D или 3D распределений элементов r и n по размерам (описания size-распределений на поверхности (r r)f, size и (n n)f, size и в объеме композита (r r r)f, size и (n n n)f, size).
Приведем пример выбора необходимых для анализа поверхности некоторого кристаллического наноразмерного квазифрактального объекта структурных состояний в виде 5х6–матрицы:
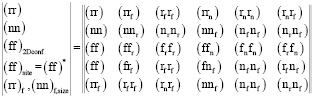 .
.
Приведем более подробные описания указанных в матрице 2D состояний.
1. Класс кристаллический, подкласс P состояния (r r):
(r r) – 2D кристалл из упорядоченных в слое цепочек асимметричных модулей,
(r rn) – 2D кристалл из упорядоченных цепочек нанофрагментов и асимметричных модулей,
(r rf) – 2D кристалл из упорядоченных цепочек локальных фракталов и асимметричных модулей,
(rn rn) – 2D кристалл из упорядоченных в слое цепочек нанофрагментов и цепочек модулей,
(rn rf) – 2D кристалл из упорядоченных цепочек локальных фракталов и нанофрагментов,
(rf rf) – 2D кристалл из упорядоченных в слое цепочек локальных фракталов.
2. Класс наноразмерный, подкласс N состояния (n n):
(n n) – 2D нанообъект из упорядоченных в слое цепочек наночастиц
(n nr) – 2D нанообъект из упорядоченных цепочек нанофрагментов структуры и наночастиц,
(n nf) – 2D нанообъект из упорядоченных цепочек нанофракталов и наночастиц,
(nr nr) – 2D нанообъект из упорядоченных в слое цепочек нанофрагментов структуры,
(nr nf) – 2D нанообъект из упорядоченных цепочек нанофрагментов структуры и нанофракталов,
(nf nf) – 2D нанообъект из упорядоченных в слое цепочек нанофракталов.
3. Класс фрактальный, подкласс F состояния (f f):
(f f) – 2D фрактальный объект из упорядоченных в слое асимметричных фракталов,
(f fr) – 2D фрактальный объект из упорядоченных в слое цепочек фрактальных фрагментов и асимметричных фракталов,
(f fn) – 2D фрактальный объект из упорядоченных в слое цепочек наноструктурированных фракталов и асимметричных фракталов,
(fr fr) – 2D фрактальный объект из упорядоченных в слое цепочек фрактальных фрагментов,
(fr fn) – 2D фрактальный объект из упорядоченных в слое цепочек фрактальных фрагментов и наноструктурированных фракталов,
(fn fn) – 2D фрактальный объект из упорядоченных в слое цепочек наноструктурированных фракталов.
4. Класс сопряженный фрактальному, подкласс F* состояния (f f)*:
(f f) – 2D фрактальный объект из упорядоченных в слое асимметричных фракталов,
(f rf) – 2D фрактальный объект из упорядоченных в слое цепочек локальных фракталов и асимметричных фракталов,
(f nf) – 2D фрактальный объект из упорядоченных в слое цепочек нанофракталов и асимметричных фракталов,
(rf rf) – 2D фрактальный объект из упорядоченных в слое цепочек локальных фракталов.
(rf nf) – 2D фрактальный объект из упорядоченных в слое цепочек локальных фракталов и нанофракталов,
(nf nf) – 2D нанофрактальный объект из упорядоченных в слое цепочек нанофракталов.
5. Класс наноразмерный, подкласс N, только состояния (n n)f:
(n nf) – 2D нанообъект из наночастиц, упорядоченных в цепочке по фрактальному закону,
(nr nf) – 2D нанообъект из нанофрагментов структуры и наночастиц, упорядоченных в цепочке по фрактальному закону,
(nf nf) – 2D нанообъект из наночастиц, упорядоченных в слое по фрактальному закону,
6. Класс кристаллический, подкласс P, только состояния (r r)f:
(r rf) – 2D кристалл из асимметричных модулей, упорядоченных в цепочке по фрактальному закону,
(rn rf) – 2D кристалл из нанофрагментов и асимметричных модулей, упорядоченных в цепочке по фрактальному закону,
(rf rf) – 2D кристалл из асимметричных модулей, упорядоченных в слое по фрактальному закону.
Дополнительными по отношению к поверхности возможными компонентами объемных структурных состояний могут быть следующие 1D объекты:
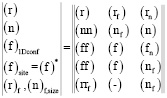
Приведем подробные описания указанных в матрице состояний 1D объектов с указанием их классовой принадлежности.
1. Класс кристаллический, подкласс P состояния (r):
(r) – 1D кристалл из упорядоченных в цепочке асимметричных модулей,
(rn) – 1D кристалл из упорядоченных в цепочке нанофрагментов,
(rf) – 1D кристалл из упорядоченных в цепочке локальных фракталов.
2. Класс наноразмерный, подкласс N состояния (n):
(n) – 1D нанообъект из упорядоченных в цепочке наночастиц,
(nr) – 1D нанообъект из упорядоченных в цепочке нанофрагментов структуры,
(nf) – 1D нанообъект из упорядоченных в цепочке нанофракталов.
3. Класс фрактальный, подкласс F состояния (f):
(f) – 1D фрактальный объект из упорядоченных в цепочке асимметричных фракталов,
(fr) – 1D фрактальный объект из упорядоченных в цепочке фрактальных фрагментов,
(fn) – 1D фрактальный объект из упорядоченных в цепочке наноструктурированных фракталов.
4. Класс сопряженный фрактальному, подкласс F* состояния (f)*:
(f) – 1D фрактальный объект из упорядоченных в цепочке асимметричных фракталов,
(rf) – 1D фрактальный объект из упорядоченных в цепочке локальных фракталов,
(nf) – 1D фрактальный объект из упорядоченных в цепочке нанофракталов.
5. Класс наноразмерный, подкласс N, только состояния (n)f:
(nf) – 1D нанообъект из наночастиц, упорядоченных в цепочке по фрактальному закону.
6. Класс кристаллический, подкласс P, только состояния (r)f:
(rf) – 1D кристалл из асимметричных модулей, упорядоченных в цепочке по фрактальному закону.
Формально учет этих дополнительных состояний для поверхности означает «гиперпространственную» поправку – учет влияния на размерный параметр <D> объемных характеристик структурного состояния материала или покрытия:
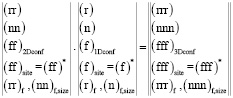 .
.
Необходимые структурные состояния – компоненты состояний в 15-мерном представлении описания – могут быть перечислены:
(r r r) – (r r r), (r r rf), (r rf rf), (rf rf rf), (r rn rf), (rn rn rf), (r r rn), (rn rf rf), (r rn rn), (rn rn rn);
(n n n) – (n n n), (n n nr), (n nr nr), (nr nr nr), (n n nf), (n nf nf), (nf nf nf), (nr nr nf), (nr nf nf), (n nr nr);
(f f f) – (f f f), (f f fn), (f fn fn), (fn fn fn), (f f fr), (f fr fr), (fr fr fr), (fr fr fn), (fr fn fn), (fn fn fn);
(f f f)* – (f f f), (f f nf), (f nf nf), (nf nf nf), (f f rf), (f rf rf), (rf rf rf), (rf rf nf), (rf nf nf), (nf nf nf);
(r r r)f – (r r rf) (r rn rf) (rn rn rf) (r rf rf) (rn rf rf) (rf rf rf);
(n n n)f – (n n nf) (n nr nf) (nr nr nf) (n nf nf) (nr nf nf) (nf nf nf).
Условный размерный параметр Di для каждого i-го структурного 3D состояния может быть рассчитан по формуле Di = 0,5(dr D(r) + df D(f) + dn D(n))i, где dr, df и dn – количества соответствующих компонент одного сорта. Значения для кристаллической компоненты D(r) = 1, для фрактальной компоненты совпадают с фрактальной размерностью:
D(f) = DimRf = Dim (GenRf) < 1,
для наноразмерной компоненты
D(n) = (<n>/no) < 1,
если средний размер нанообъекта <n> меньше, чем no = 100 нм [6].
Пример методики расчета размерного параметра <D>. Для предполагаемого структурного 2D состояния поверхности некоторого композиционного материала
[(rn rf), (nn nf), (fr fn)2D conf, (rf nf)site, (rn rf)f, (nn nf)f size]
и связанного с ним 3D состояния в объеме
[(rn rf rn), (nn nf nn), (fr fn fn)3D conf, (rf nf nf)site, (rn rf rf)f,(nn nf nf)f size]
имеем:
– среднее значение параметра для 2D состояния
<D>2D = (1/12)(6 D(r) + 10 <D(n)> + +8 <D(f)>) = 0,5 + (5/6) <D(n)1> + +(2/3) <D(f)1>,
– среднее значение параметра для 3D состояния
<D>3D = (1/12)(8 D(r) + 16 <D(n)> + +12 <D(f)>) = (2/3) + (4/3) <D(n)1> + +<D(f)2>.
Тогда среднее значение параметра только для третьих координат 3D состояния
<D>1D = (1/12)(2 D(r) + 6 <D(n)> + +4 <D(f)>) = (1/6) + 0,5 <D(n)2> + +(1/3) <D(f)3>,
а среднее значение параметра для поверхности с учетом объемной поправки
<Dповерхности> = (2/3)(<D>2D + <D>1D).
Таким образом, в зависимости от возможного «продолжения» поверхности композиционного материала (кристалл, нанообъект, квазифрактал) в третьем («гиперпространственном») измерении эффективное значение размерного параметра <Dповерхности> может отличаться от формального значения <D>2D. Отметим, что результаты анализа возможных видов структурных состояний и оценка размерного параметра необходимы для учета его возможного влияния на некоторые аддитивные поверхностные свойства соответствующего композиционного материала. В частности, отклонение значения параметра для анализируемого многофазного объекта (за счет ультрадисперсного состояния и квазифрактальной конфигурации межфазных границ) от величины мерности пространства, в котором этот объект существует, может обусловить эффект синергизма свойств компонентов [10, 13 – 15, 18].
Выводы
Рассмотрены возможности гиперпространственного представления структурных состояний поверхности композиционных материалов и покрытий для анализа величины эффективного размерного параметра, определяющего отклонение аддитивных поверхностных свойств материалов от соответствующих его объемных свойств. Представление включает символьные описания структурных состояний кристаллической (r r) и наноразмерной ((n n) компонент, вероятных квазифрактальных конфигураций межфазных границ (f f)2Dconf, квазифрактальных size-распределений (f f)*size и site-распределений ((r r)f + (n n)f)site элементов на поверхности композита. Установлено, что некоторые из проанализированных вариантов комплексных состояний могут быть результатом реализации определенного фазово-разупорядоченного состояния поверхности композиционных материалов и покрытий и использованы при оценке величины синергического эффекта проявления антифрикционных свойств компонентами композита при трении и износе.

