В современных условиях в процессе обучения все чаще используется вычислительная техника, позволяющая студентам проводить сложные расчеты с применением различных компьютерных программ. Достаточно удобной программой для обучения, вычислений и визуализации результатов математического моделирования инженерных расчетов является Mathcad.
Учебно-методическое пособие «Применение системы Mathcad для решения задач по линейной алгебре» разработано и подготовлено к изданию кандидатом физико-математических наук, доцентом кафедры «Высшая и прикладная математика» Уральского государственного университета путей сообщения (УрГУПС) Натальей Валерьевной Медведевой.
Настоящее пособие разработано в соответствии с требованиями федерального государственного образовательного стандарта высшего образования направления 15.03.06 – «Мехатроника и робототехника» (уровень бакалавриата) и может быть рекомендовано студентам технических специальностей или направлений подготовки бакалавров. Пособие может быть полезным при проведении лекционных, практических и лабораторных занятий, а также контрольных мероприятий по дисциплине Б1.Б.4. – «Математика».
Учебно-методическое пособие направлено на формирование у студентов способности к самообразованию и самоорганизации, умения применять математические методы и вычислительную технику для решения практических задач.
Содержание пособия последовательно знакомит читателей с основными средствами пакета Mathcad, которые применяются для решения задач раздела «Линейная алгебра» при изучении дисциплины Б1.Б.4. – «Математика». Пособие содержит восемь лабораторных работ.
В ходе выполнения лабораторной работы № 1 студенты знакомятся с основами работы в программе Mathcad, с работой текстового и формульного редактора. Лабораторные работы № 2-№ 8 содержат теоретический материал, методику аналитического и компьютерного выполнения заданий, задания для самостоятельной работы по соответствующим темам раздела: «Матрицы и действия над ними», «Определители. Обратная матрица», «Решение систем линейных алгебраических уравнений по формулам Крамера», «Матричные уравнения. Решение систем линейных алгебраических уравнений методом обратной матрицы», «Исследование систем линейных алгебраических уравнений», «Решение систем линейных алгебраических уравнений методом Гаусса», «Однородные системы линейных алгебраических уравнений». Структура лабораторных работ позволяет использовать пособие для самостоятельной работы студентов.
Содержащиеся в пособии теоретические сведения и примеры выполнения заданий могут помочь студентам при повторении материала и подготовке к тестированию, как в рамках внутреннего контроля, так и по программам федерального государственного образовательного стандарта высшего образования. Приведем примеры некоторых заданий, способствующие достижению данной задачи.
Пример 1. Найти А•B, B•A, если
, 
.
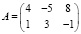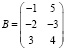Пример 2. Вычислить определители следующих матриц
а)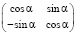 
;
б) 
.
Пример 3. Найти матрицу, обратную к матрице
.
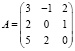Пример 4. Найти ранг матрицы
.
Пример 5. Исследовать систему уравнений
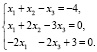
Пример 6. Найти базисное и частное решение системы уравнений
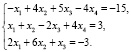
Для организации самостоятельной работы обучающихся в пособии также приведены индивидуальные задания – шесть заданий по 40 вариантов каждое. Приведем примеры заданий.
Задание 1. Решить матричное уравнение:
.
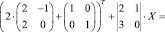
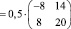Задание 2. Составить и решить систему линейных уравнений AX = B относительно матрицы X: а) методом Крамера; б) методом обратной матрицы; в) методом Гаусса, если
, 
.
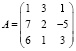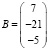Задание 3. Матричное уравнение DX = C записать в виде системы линейных уравнений и решить по формулам Крамера и методом обратной матрицы:
,
.
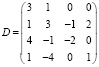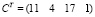Задание 4. Решить матричное уравнение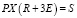 
относительно матрицы X:
,
,
.
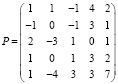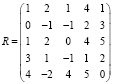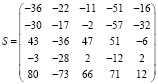Результат проверить умножением.
Задание 5. Матричное уравнение PX = Q записать в виде системы линейных уравнений и решить ее методом Гаусса. Результат проверить умножением:
,
.
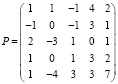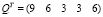Задание 6. Исследовать и решить системы однородных уравнений:
а)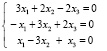 
,
б)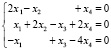 
.
В зависимости от уровня сформированности у студентов практических умений решения задач можно составлять разной степени сложности индивидуальные домашние задания, типовые расчеты. Например, одной учебной группе для самостоятельной работы можно выдать задания № 1, № 2, № 6, для группы с более высоким уровнем обученности – задания № 1, № 2, № 3, № 5, № 6. При этом аналитическое решение заданий, содержащих матрицы высоких размерностей, можно сопровождать компьютерным решением в системе Mathcad.
Список использованной в пособии литературы [1 – 4] также может помочь студентам при работе с материалом раздела «Линейная алгебра».
Данное пособие способствует достижению одной из задач освоения дисциплины Б1.Б.4 – «Математика»: освоение математического аппарата, являющегося теоретической основой современного инжиниринга, его практических приложений и приобретение навыков работы с ними.
Пособие положительно оценено рецензентами: кандидатом физико-математических наук, доцентом, старшим научным сотрудником Института математики и механики Уральского отделения Российской академии наук В.Л. Розенбергом и кандидатом физико-математических наук, доцентом кафедры «Высшая и прикладная математика» Уральского государственного университета путей сообщения П.П. Скачковым.