Современные информационные и коммуникационные технологии, предоставляя широкие возможности для создания и внедрения эффективных методов и форм обучения, основанных на их применении, являются одной из основных составляющих предмета подготовки студента – будущего специалиста. Вопросы, посвященные компьютерно-ориентированным методикам изучения различных тем школьного и вузовского курсов математики, рассматриваются в работах Е.В. Ашкинузе, Я.А. Ваграменко, Ю.С. Брановского, С.Г. Григорьева, В.В. Гриншкуна, В.П. Дьяконова, В.А. Далингера, Г.Л. Луканкина, В.Р. Майера, И.В. Роберт, А.В. Якубова и др.
Продуктивность использования информационных технологий в обучении стохастике (теории вероятностей и математической статистике) обеспечивается реализацией совокупности условий, которые способствуют включению студентов в активную и многовариантную учебную деятельность, формированию их стохастической и информационной культуры в активную и многовариантную учебную деятельность, формированию их стохастической и информационной культуры [5].
По нашему мнению, при изучении студентами теории вероятностей и математической статистики значительно повысить качество результатов обучения позволит использование универсального математического пакета Mathcad, предназначенного для выполнения инженерных и научных расчетов [1-4]. Целесообразность его применения при решении вероятностных и статистических задач обоснована нами в работе [5].
Рассмотрим более подробно возможности применения Mathcad при изучении темы «Непрерывные случайные величины».
Так, для введения нужной функции плотности вероятности достаточно удобно использовать окно Insert Function (сочетание клавиш [Ctrl]+[Shift]+[F]), в котором требуемые встроенные функции находятся в списке Probability Density (Плотность вероятности). Известно, что для вычисления функции распределения можно найти посредством интегрирования плотности вероятности. Благодаря наличию в Mathcad специальной встроенной функции pnorm(x, m, s) можно производить необходимые вычисления, не находя «неберущийся» сложный несобственный интеграл.
Посредством встроенной функции dnorm (x, s, a) (приставка d от англ. density – плотность) вычисляется плотность нормального распределения. Плотность вероятности р(х) и теоретическая функция распределения F(х) стандартного нормального распределения находят таким образом:
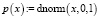
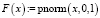
Большое значение для усвоения понятий плотности распределения и функции распределения случайной величины, их свойств имеет геометрическая интерпретация, обеспечивающая, главным образом, развивающую функцию обучения, высокую умственную активность, пространственное и геометрическое мышление студентов.
В MathCAD для стандартного нормального распределения имеются следующие встроенные функции, благодаря которым можно вычислить квантили:
qnorm(0.5, 0, 1) = 0 – медиана;
qnorm(0.25, 0, 1) = -0.674 – нижняя квартиль;
qnorm(0.75, 0, 1) = 0.674 – верхняя квартиль;
qnorm(0.95, 0, 1) = 1.645 – 0.95-квантиль.
Для того чтобы вычислить вероятность попадания случайной величины в некоторый интервал посредством использования нормированной функции распределения (при дисперсии s2 и математическом ожидании а), как правило, используют затабулированную функцию Лапласа – нормированную функцию вероятности (полагают а = 0, s = 1). При решении подобных задач посредством пакета не требуется применять нормированные функции вероятности в связи с тем, в данную систему уже встроены алгоритмы численного интегрирования, позволяющие быстро вычислить функцию распределения в стандартном виде. Если же задачу необходимо решить традиционным способом, то в данном случае можно применить cnorm(x) – специальную встроенную функцию, в основе которой лежит формула Лапласа.
Значение нормальной функции распределения с математическим ожиданием, равным нулю и среднеквадратическим отклонением, равным единице, вычисляется с помощью функции pnorm(x, 0, 1).
Для показательного распределения плотность вероятности можно найти в MathCAD, используя специальную функцию dexp(х, l), а функцию распределения – при помощи рехр(х, l) (рис. 1).
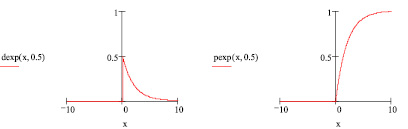
Рис. 1
Математическое ожидание и дисперсию показательного распределения можно вычислить, используя средства аналитического интегрирования.
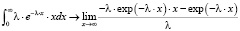 .
.
Символьное вычисление параметров показательного распределения: математического ожидания
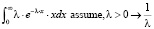
и дисперсии
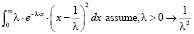
При этом необходимо в обоих случаях ввести на величину параметра λ какое-либо ограничение посредством оператора Assume панели Symbolic. Если этого не сделать, получим некорректные результаты в виде общих выражений с пределами, причем в случае дисперсии результат будет очень большим.
Рассмотрим следующий пример. Дана двумерная случайная величина (ξ, η), равномерно распределенная в круге x2 + y2 ≤ 1. Требуется найти плотности вероятности компонент данной случайной величины и построить графики. Найти условные плотности вероятностей величины х при у = 0; 0,5; 0,8 и построить графики.
Решение. Сначала вычислим плотность вероятностей случайной величины (ξ, η).
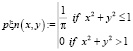
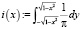
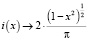
В пакете вычисления по формулам осуществляются одновременно с их набором. Переменные, формулы, а также параметры можно изменять, наблюдая мгновенно изменения результата вычислений.
Найдем распределение плотности вероятностей величины ξ
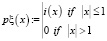
Вычислим распределение плотности вероятностей величины η
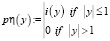
Строим графики (рис. 2).

Рис. 2
Условное распределение плотности вероятностей
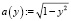
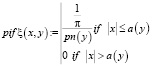
Строим график (рис. 3).
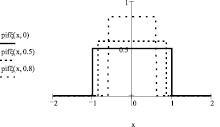
Рис. 3
Таким образом, грамотное использование математических пакетов в стохастической подготовке значительно повышает производительность процесса обучения, позволяет сформировать у студентов адекватное представление о месте, роли и широких возможностях современных информационных технологий при решении самых разнообразных задач теории вероятностей.

