Описание необходимости комплексного пространства
Покажем, что собственное значение оператора импульса может быть комплексным. Радиальная проекция оператора импульса определяется по формуле
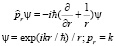 .
.
При комплексном значении 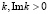 , получаем комплексное, ограниченное значение эрмитова оператора. Справедливость формулы для радиальной проекции оператора импульса следует из соотношения
, получаем комплексное, ограниченное значение эрмитова оператора. Справедливость формулы для радиальной проекции оператора импульса следует из соотношения
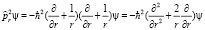
Причем как доказано в [9] задача 59, эта проекция оператора импульса является эрмитовой в действительном пространстве, но ничто не мешает определить собственное число комплексным, с положительной мнимой частью. В комплексном пространстве для волновой функции надо ввести область определения.
Покажем, что собственное значение энергии может быть комплексным. Так для ямы постоянной глубины U0 размером a, см. задачу в [1] к параграфу §22. Вне ямы решение имеет вид 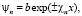
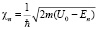 . Внутри ямы решение ищем в виде
. Внутри ямы решение ищем в виде
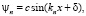
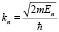 .
.
Условие непрерывности волновых функций 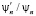 на границе ямы, определяет решение
на границе ямы, определяет решение
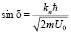
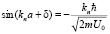
Вычисления надо производить аккуратно, с учетом всех тонкостей периодических функций. При этом имеем одинаковые ветви у арксинуса
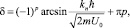
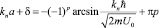 .
.
При условии p нечетном, получаем уравнение, где в неявном виде задано значение энергии
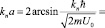
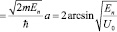 (1.1)
(1.1)
Откуда определится конечное число действительных и счетное количество комплексных значений энергии En во всем пространстве. Комплексное значение En получается при значении аргумента у арксинуса больше единицы.
При комплексной энергии образуются квазистационарные состояния с комплексной волновой функцией. Это состояние продлится не долго, частица перейдет на действительные уровни энергии. Обозначим
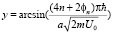 ,
,
перепишем эту формулу для аргумента, больше единицы
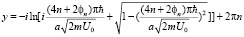 ,
,
откуда имеем
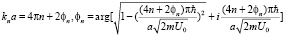 .
.
Где величина n определится из нелинейного уравнения.
Для комплексного корня имеем значение
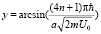
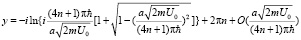 ,
,
где для арксинуса использовано главное значение, как для квадратного корня, а для образовавшегося логарифма имеется счетное количество ветвей. Асимптотика решения для комплексного корня равна
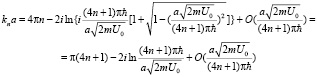 .
.
Причем для комплексного корня при большом значении n выполняется
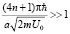 .
.
Т.е. имеем
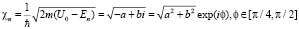 ,
,
при условии, что мнимая часть b положительная. При этом вне стационарной ямы знак величины b определяется знаком 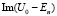 , т.е. этот знак положителен в силу отрицательной мнимой части у величины
, т.е. этот знак положителен в силу отрицательной мнимой части у величины
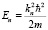 .
.
Имеем условие 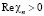 в силу условия на фазу n, и значит, затухание сохранится при колебательном решении. При этом ветви всех функций, входящих в одну формулу, одинаковы. Внутри стационарной ямы волновая функция равна
в силу условия на фазу n, и значит, затухание сохранится при колебательном решении. При этом ветви всех функций, входящих в одну формулу, одинаковы. Внутри стационарной ямы волновая функция равна
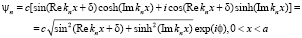 .
.
Получается, что комплексное решение при любом n имеет физический смысл.
Мнимое время и комплексная траектория используется в квантовой механике. Так в задаче № 3 к §77 см. [1] определено мнимое время
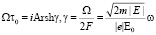 ,
,
где 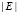 – энергия связи электрона в яме, E0 амплитуда переменного электрического поля, частота этого переменного поля. «Мнимость момента времени 0 выражает собой классическую неосуществимость процесса». Где плотность вероятности считается по формуле
– энергия связи электрона в яме, E0 амплитуда переменного электрического поля, частота этого переменного поля. «Мнимость момента времени 0 выражает собой классическую неосуществимость процесса». Где плотность вероятности считается по формуле
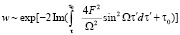 .
.
Наличие в плотности вероятности мнимого значения 0 говорит о зависимости дисперсии времени от величины Im0, т.е. о колебании времени в зависимости от метрического интервала с амплитудой, зависящей от величины Im0.
Т.е. в микромире возможно использование мнимого времени, что и делается далее по тексту.
Метод комплексной траектории используется как математический прием для определения коэффициента отражения от барьера §52 см. [1]. Также используется комплексное время при описании перехода под влиянием адиабатических возмущений см. [1] §53. В этих двух случаях дисперсия координаты и времени определяется плотностью вероятности, и соответствует мнимым координатам и времени. Дисперсия определяет колебание координат и времени с амплитудой, зависящей от мнимой компоненты координаты и времени.
Чем же это объясняется? Дело в том, что модель действительного пространства для объяснения всех эффектов квантовой механики не достаточна. Возникают комплексные собственные значения. Значит надо строить модель квантовой механики в комплексном пространстве. При этом операторы импульса во всем комплексном пространстве не будут эрмитовые. Докажем, что оператор импульса не эрмитов в комплексном пространстве. Он равен
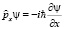 ,
,
для чего вычислим скалярное произведение, оно окажется равным в случае действительного пространства
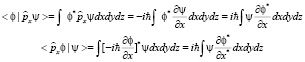 .
.
Если пространство действительно, то получим равенство скалярных произведений, и значит оператор импульса эрмитов. Но если пространство комплексное, то равенства выражений не будет и оператор импульса будет не эрмитов. Аналогичное доказательство можно реализовать для оператора координаты
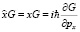
в импульсном представлении. Оказывается, в комплексном пространстве операторы, импульса и координаты являются операторами антисимметричными, и не являются эрмитовыми.
Для оператора энергии в [1]§8 доказывается, что справедливо равенство
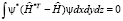 ,
,
для произвольных функций ?. Но в комплексном пространстве
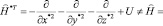
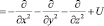 ,
,
таким образом определенный гамильтониан не является эрмитовым в комплексном пространстве, а является эрмитовым в действительном пространстве. Т.е. оператор
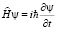
в комплексном пространстве не является эрмитовым. Определение энергии комплексной во втором примере, говорит о том, что действительное пространство не описывает все свойства квантовой механики, и надо строить квантовую механику в комплексном пространстве.
При использовании этих собственных функций возникает проблема выбора контура интегрирования или рассмотрения области комплексного пространства, в которых эти функции ограничены. Область определения для каждой собственной функции находится индивидуально.
При этом операторы энергии, и времени являются симметричными, а операторы импульса и координаты антисимметричны. При этом скалярное произведение нужно использовать без использования комплексного сопряжения. Доказательство аналогично доказательству эрмитовости операторов в действительном пространстве, только вместо эрмитова сопряжения нужно использовать транспонирование и доказательство антисимметричности операторов проходит и в комплексном пространстве. Это позволяет для этих операторов построить ортогональный базис для симметричных и антисимметричных операторов. Докажем это. Выберем у симметричной матрицы два собственных значения и собственных вектора
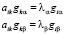 .
.
Умножим первое из этих равенств на величину gi, а второе равенство на величину gi, получим
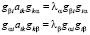 . (1.2)
. (1.2)
Транспонируем второе равенство (1.1), получим
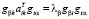 (1.3)
(1.3)
В случае симметричного оператора имеем 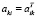 и имеем одинаковые выражения в левой части первого уравнения (1.2) и (1.3). Вычитаем из первого уравнения (1.2) уравнение (1.3), получим
и имеем одинаковые выражения в левой части первого уравнения (1.2) и (1.3). Вычитаем из первого уравнения (1.2) уравнение (1.3), получим
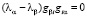 .
.
Значит собственные векторы, соответствующие разным собственным числам симметричного оператора ортогональны.
В случае антисимметричного оператора получим 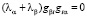 , откуда следует ортогональность собственных векторов при условии
, откуда следует ортогональность собственных векторов при условии 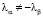 .
.
При этом ортогональные собственные векторы образуют базис
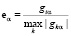 ,
,
который не является нормированным. Собственные векторы определяются с точностью до множителя, поэтому их можно нормировать для удобства вычислений на максимальное значение. Это допущение основано, на том, что условие 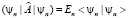 при условии
при условии 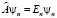 можно разрешить с помощью предельного перехода вне зависимости от нормы
можно разрешить с помощью предельного перехода вне зависимости от нормы 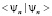 .
.
Собственное значение в случае дискретного спектра не зависит от нормы собственного вектора. В самом деле, из равенства 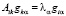 следует значение собственного числа
следует значение собственного числа 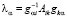 вне зависимости от значения нормы собственного вектора. При этом, в случае
вне зависимости от значения нормы собственного вектора. При этом, в случае 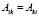 собственные векторы ортогональны, и значит,
собственные векторы ортогональны, и значит, 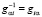 . Причем любой симметричный оператор в случае дискретного спектра можно представить в виде
. Причем любой симметричный оператор в случае дискретного спектра можно представить в виде 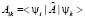 и значит, его собственное число не зависит от нормы собственного вектора. Отметим, что в случае симметричного или антисимметричного оператора можно построить ортогональный базис, а в случае оператора общего вида собственные векторы могут быть не ортогональны. При этом собственное число все равно можно определить, используя обратную матрицу. Существует теорема, что в случае разных собственных значений у квадратной матрицы Aik размерности N, существуют N независимых собственных вектора см. [7] §8, и значит, определитель, составленный из матрицы собственных векторов не нулевой, и матрица, обратная матрице из собственных векторов существует.
и значит, его собственное число не зависит от нормы собственного вектора. Отметим, что в случае симметричного или антисимметричного оператора можно построить ортогональный базис, а в случае оператора общего вида собственные векторы могут быть не ортогональны. При этом собственное число все равно можно определить, используя обратную матрицу. Существует теорема, что в случае разных собственных значений у квадратной матрицы Aik размерности N, существуют N независимых собственных вектора см. [7] §8, и значит, определитель, составленный из матрицы собственных векторов не нулевой, и матрица, обратная матрице из собственных векторов существует.
При этом в случае бесконечного количества собственных значений, выражение для собственного числа 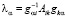 может расходиться, тогда определять собственное число надо с помощью предельного перехода, в случае нулевой нормы
может расходиться, тогда определять собственное число надо с помощью предельного перехода, в случае нулевой нормы 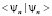 . Но если предельный переход определит собственное число, значит, и сумма в формуле
. Но если предельный переход определит собственное число, значит, и сумма в формуле 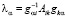 будет сходящейся, так как
будет сходящейся, так как 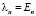 .
.
Условие существования ортогонального базиса не является необходимым для существования собственного числа, достаточно чтобы собственные векторы были независимы. В случае дискретного спектра, выбрав независимую систему функций можно определить матрицу этого преобразования 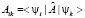 , а значит, и вычислить спектр для матрицы общего вида с разными собственными значениями.
, а значит, и вычислить спектр для матрицы общего вида с разными собственными значениями.
В случае непрерывного спектра 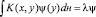 , задачу можно свести к нахождению собственного числа с помощью преобразования
, задачу можно свести к нахождению собственного числа с помощью преобразования
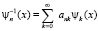 ,
,
где 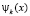 система собственных функций. Причем использовать скалярное произведение без знака комплексного сопряжения. Коэффициенты ank определятся из формул
система собственных функций. Причем использовать скалярное произведение без знака комплексного сопряжения. Коэффициенты ank определятся из формул
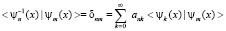 ,
,
матрица, обратная к матрице 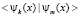 существует, в силу независимости функций ее образующих. Определитель матрицы
существует, в силу независимости функций ее образующих. Определитель матрицы 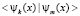 называется определителем матрицы Грама и не равен нулю в случае независимых функций
называется определителем матрицы Грама и не равен нулю в случае независимых функций 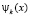 . При этом имеем
. При этом имеем 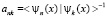 . Тогда собственное число равно
. Тогда собственное число равно
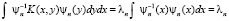 .
.
При этом необходимо отказаться от условия нормировки волновой функции на единичное значение, а использовать понятие независимые векторы и ортогональные векторы.
Определим физический смысл корня из квадрата наблюдаемой в комплексном пространстве
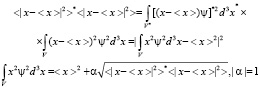 .
.
Причем при условии 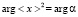 , имеем
, имеем
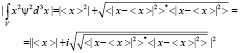 .
.
Или имеем
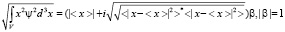
Величина 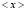 и величина
и величина 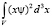 в комплексном пространстве является комплексной. Корень из квадрата наблюдаемого значения координаты величина комплексная, и определяется по формуле, так как величина
в комплексном пространстве является комплексной. Корень из квадрата наблюдаемого значения координаты величина комплексная, и определяется по формуле, так как величина 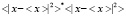 действительна. Причем получается формула при условии
действительна. Причем получается формула при условии 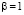
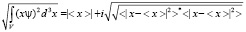 . (1.4)
. (1.4)
Т.е. действительная часть среднего квадрата комплексной величины равна модулю среднего значения величины, а мнимая часть среднеквадратическому отклонению.
Имеется необходимость к переходу в комплексное пространство. Действительные собственные значения энергии, импульса и координаты описывают точечные частицы. Мнимая часть этих параметров описывает распределение в пространстве. При этом рождение и уничтожение частиц происходит в области, равной, по крайней мере, комптоновской длине волны. Значит, параметры частиц должны быть распределенными, т.е. иметь мнимую часть, которая описывает отклонение от среднего значения. Кроме того, большинство процессов в квантовой механике не стационарно. Излучение электромагнитной волны сопровождается переходом с одного собственного состояния на другое собственное состояние. Этот переход описывается мнимой частью комплексной энергии. Каков же физический смысл мнимой части комплексного значения параметра в микромире? Мнимая энергия и импульс определяют затухание волновой функции по формуле
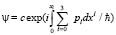 .
.
Комплексный размер системы также определяет затухание ее волновой функции или ее пульсации с амплитудой, равной мнимой части параметра. При этом путь интегрирования по комплексному пространству будет описан ниже по тексту. Комплексное собственное значение импульса локализует частицу вблизи действительного собственного значения. Мнимая часть собственной координаты описывает распределение частицы в пространстве. Собственное значение времени определяется с ошибкой, т.е. с мнимой частью и является комплексным. Мнимая часть собственного значения времени характеризует длительность реакции, или время преодоления барьера. Среднее значение действительного интервала времени описано в статье [2]. Причем пространство в этой статье описано как комплексное.
Кроме того, комплексное пространство без ввода новых членов в уравнение, описывает диссипацию энергии. В действительном пространстве для описания диссипации энергии надо вводить дополнительные константы, что является недостатком теории.
Волновую функцию в случае комплексного решения надо представлять в виде степеней комплексной переменной z
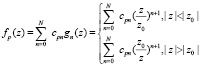 .
.
Вычислим вектор-функцию fp(z), имеющую ортогональные значения остальным 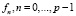 . Рассмотрим совокупность независимых векторов fp, образующих подпространство S. Пусть f произвольный вектор, линейно независимый от данного подпространства. Докажем, что вектор f можно единственным образом представить в виде
. Рассмотрим совокупность независимых векторов fp, образующих подпространство S. Пусть f произвольный вектор, линейно независимый от данного подпространства. Докажем, что вектор f можно единственным образом представить в виде
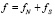 ,
,
где 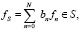 вектор fN ортогонален S. Тогда имеем
вектор fN ортогонален S. Тогда имеем 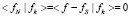 . Причем величина fN определяется с точностью до множителя. Подставляя значение fS получим систему уравнений
. Причем величина fN определяется с точностью до множителя. Подставляя значение fS получим систему уравнений
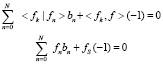
Получаем систему линейных уравнений относительно не нулевых величин 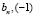 . Значит, определитель этой системы линейных уравнений равен нулю. Из равенства нулю определителя этой системы линейных уравнений определяется значение fS, а значит и величину
. Значит, определитель этой системы линейных уравнений равен нулю. Из равенства нулю определителя этой системы линейных уравнений определяется значение fS, а значит и величину 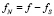 . Причем при вычислении этого значения необходимо разделить на определитель матрицы Грама, равный
. Причем при вычислении этого значения необходимо разделить на определитель матрицы Грама, равный 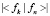 . Этот определитель не равен нулю в силу линейной независимости векторов fk.
. Этот определитель не равен нулю в силу линейной независимости векторов fk.
Таким образом, определено направление вектора fp, ортогональное векторам 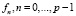 используя только понятие независимости векторов и свойства определителя Грама. Это сделано без использования понятия нормировки вектора.
используя только понятие независимости векторов и свойства определителя Грама. Это сделано без использования понятия нормировки вектора.
Существует теорема линейной алгебры, что всякий невырожденный ряд векторов можно ортогонализировать. Процесс ортогонализации приводит к векторам, определяемым однозначно с точностью до множителя см. [8]§6.
Таким образом, определим ортогональные функции fp(z). Нормируем эти функции, разделив на интеграл 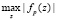 для удобства вычисления вектора, ортогональные функции можно определить с точностью до множителя. Возможность такой нормировки описана выше по тексту.
для удобства вычисления вектора, ортогональные функции можно определить с точностью до множителя. Возможность такой нормировки описана выше по тексту.
Эта функция непрерывна при характерном размере задачи 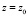 , но производная от этой функции в этой точке рвется. В случае атома водорода за характерный размер надо брать радиус Бора. Тогда k волновую функцию определим по формуле
, но производная от этой функции в этой точке рвется. В случае атома водорода за характерный размер надо брать радиус Бора. Тогда k волновую функцию определим по формуле
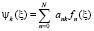 .
.
Для получения точного решения необходимо устремить количество членов ряда к бесконечности. Но практическое решение содержит конечное число членов ряда. Решаем уравнение Шредингера для этой безразмерной волновой функции, и определяем для каждого k состояния величину ank. В случае одномерного уравнения Шредингера оно записывается в виде
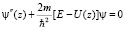 .
.
Подставляем в это уравнение решение в виде 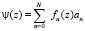 , умножаем уравнение на величину
, умножаем уравнение на величину 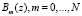 , и интегрируем по комплексной переменной, начиная с параметра 0 до бесконечности, причем контур интегрирования проходит через точку
, и интегрируем по комплексной переменной, начиная с параметра 0 до бесконечности, причем контур интегрирования проходит через точку 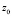 . Получаем уравнение (приведя его к безразмерному виду)
. Получаем уравнение (приведя его к безразмерному виду)
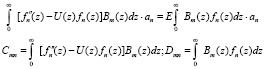 .
.
Полагаем 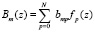 . Получим уравнения
. Получим уравнения 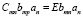 в силу ортогональности функций fp(z). Для получения ортонормированного базиса надо добиться
в силу ортогональности функций fp(z). Для получения ортонормированного базиса надо добиться 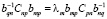 , путем выбора Bm(u). Для нахождения коэффициентов bmp необходимо решить уравнение
, путем выбора Bm(u). Для нахождения коэффициентов bmp необходимо решить уравнение
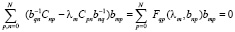 ,
,
т.е. по матрице 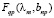 определить вектор bmp. Чтобы задача имела решение, определитель этой системы должен равняться нулю, т.е. должно существовать число m, чтобы определитель равнялся нулю, при этом определится вектор bmp, и вновь надо считать собственное число m, уточнив матрицу
определить вектор bmp. Чтобы задача имела решение, определитель этой системы должен равняться нулю, т.е. должно существовать число m, чтобы определитель равнялся нулю, при этом определится вектор bmp, и вновь надо считать собственное число m, уточнив матрицу
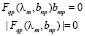
Далее получаем уравнение на определение координат ортонормированного базиса, где 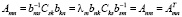 . Для каждого m получаем свое решение
. Для каждого m получаем свое решение
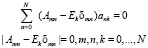 .
.
Которое имеет N + 1 комплексное решение. Так как 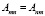 комплексные собственные вектора ank образуют ортогональный базис с комплексными собственными значениями Ek.
комплексные собственные вектора ank образуют ортогональный базис с комплексными собственными значениями Ek.
Получаем N + 1 ортогональные собственные векторы ank, n, k = 0,…, N, соответствующие собственным значениям энергии Ek, k = 0,…, N.
При этом получим набор независимых собственных функций
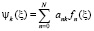 .
.
В самом деле, при этом получается, что собственное значение равно
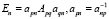
в силу симметрии 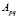 . Так как собственные функции независимы, получаем
. Так как собственные функции независимы, получаем
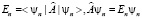 ,
,
что следует из формулы
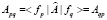 .
.
Эта функция симметрична по построению. Откуда имеем
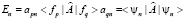 .
.
При этом в точках, удовлетворяющих условию
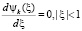 ,
,
и соответствующих 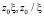 наблюдается сгущение частиц. При этом
наблюдается сгущение частиц. При этом 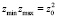 .
.
Опишем физический смысл волновой функции. Для этого покажем, что уравнение Шредингера сводится к уравнению Навье – Стокса. Докажем это. Для чего запишем уравнение Шредингера и преобразуем его с помощью формулы
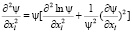
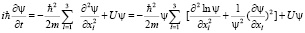 .
.
Разделив на массу m, получим уравнение
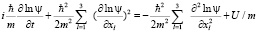 .
.
Получим уравнение в частных производных, взяв градиент от обеих частей уравнения, введем действительную скорость по формуле
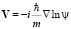 .
.
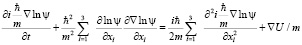 .
.
Подставляя значение скорости в преобразованное уравнение Шредингера, получим
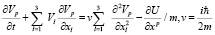 .
.
Получим трехмерное уравнение Навье – Стокса с давлением, соответствующим потенциалу и с комплексной скоростью, удовлетворяющей условию
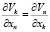 .
.
Физический смысл логарифма волновой функции – это потенциал скорости частиц с массой m, для среды с кинематической вязкостью
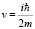 ,
,
где m масса частиц, образующих эту среду.
В случае свободного поля нормировка определяется по формуле
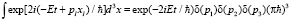 .
.
При этом областью определения волновой функции является действительная ось. При этом величина средней координаты равна
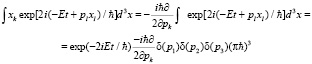
нормировав эту величину, вводя аппроксимацию для дельта функции, получим
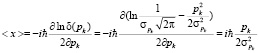 .
.
Где величина 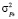 это дисперсия импульса. Если в качестве
это дисперсия импульса. Если в качестве 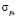 взять величину
взять величину 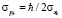 , где величина
, где величина 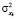 , это дисперсия координаты, то получим для среднего значения координаты
, это дисперсия координаты, то получим для среднего значения координаты
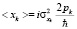 .
.
При рассмотрении чисто действительного пространства величина среднего равна бесконечности.
В случае 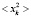 получим значение (под значком
получим значение (под значком 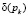 будем подразумевать аппроксимацию дельта функции)
будем подразумевать аппроксимацию дельта функции)
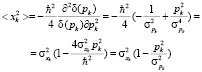
В комплексном пространстве возможен отрицательный средний квадрат. Корень из среднего квадрата координаты для большого импульса величина мнимая и равна 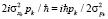 . Эта величина среднего квадрата координаты для одной частицы в свободном пространстве. Дисперсия координаты равна
. Эта величина среднего квадрата координаты для одной частицы в свободном пространстве. Дисперсия координаты равна
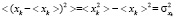 .
.
При этом, если средний квадрат, среднее значение и дисперсия удовлетворяют равенству
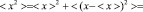
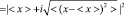 .
.
Извлекая корень из этого равенства, получим
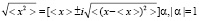 .
.
Данное определение среднего и среднего квадрата получено путем умножения на мнимую единицу определенных комплексных значений при условии
= 1 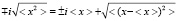 .
.
Взяв квадрат модуля этой величины, получим 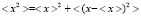 , т.е. правильную формулу по определению среднего квадрата. Но это соотношения между средними величинами соответствует возможным комплексным значениям макромира, и для микромира не выполняется. Для микромира справедливо соотношение (1.4).
, т.е. правильную формулу по определению среднего квадрата. Но это соотношения между средними величинами соответствует возможным комплексным значениям макромира, и для микромира не выполняется. Для микромира справедливо соотношение (1.4).
Переход в комплексное пространство не меняет значение энергии для атома водорода и гармонического осциллятора, так как вычисленное значение энергии действительно при действительных волновых функциях, следовательно, определение скалярного произведения не меняется.
Электрон, как квантовая система имеет размытые границы, которые имеют среднеквадратическое отклонение , при этом напряженность поля электрона равна
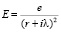 .
.
Электромагнитная масса электрона равна
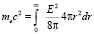 .
.
Значение электромагнитной массы электрона
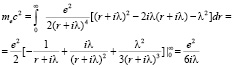
Физический смысл комплексного решения – это его модуль, откуда имеем величину среднеквадратичного отклонения радиуса электрона 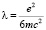 . Эта величина соответствует границе комплексного радиуса электрона. Предел применимости электродинамики несколько больше и равен
. Эта величина соответствует границе комплексного радиуса электрона. Предел применимости электродинамики несколько больше и равен 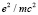 см. [3]§75, т.е. можно сказать, что классическая электродинамика применяется в действительном пространстве.
см. [3]§75, т.е. можно сказать, что классическая электродинамика применяется в действительном пространстве.
Упрощение вычислений в комплексном пространстве
В комплексном пространстве возможно описание скалярного поля без использования перенормировок. Перенормировки в квантовой теории поля возникли из-за стремления действительного решения к бесконечности, при наличии комплексных координат положения равновесия. Ставится задача определить энергию простейшей системы, для которой используется перенормировка. Т.е. определить функцию плотности Лагранжа скалярного поля, которая в случае комплексного скалярного поля имеет вид
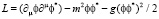 .
.
При этом тензор плотности энергии и импульса равен
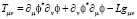 .
.
При этом плотность энергии и импульса равна
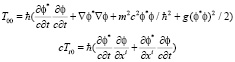
Тензор энергии и импульса является действительным. При этом поле имеет размерность 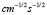 .
.
А импульс и энергия поля равны
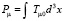 .
.
При этом как показано в начале статьи собственные значения энергии и импульса могут быть комплексные. Значит, определение действительной функции плотности Лагранжа не включает комплексное значение и является ошибочным. Функция плотности Лагранжа надо определять без учета комплексно сопряженных членов в виде
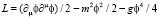 . (2.1)
. (2.1)
Функция плотности Лагранжа (2.1) сводится к уравнению с комплексным скалярным квантовым полем и к уравнению, определяющему критическую фазу функционального интеграла
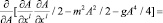
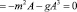 .
.
Должны выполняться равенства
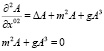 (2.2)
(2.2)
Получим его решение с помощью метода Галеркина путем подстановки
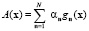 .
.
Причем функции 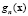 должны удовлетворять уравнению
должны удовлетворять уравнению 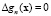 .
.
В качестве базисных функций можно выбрать абсолютно сходящиеся при конечных коэффициентах n при условии r > a сферические функции
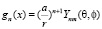 .
.
Подставляем в первое уравнения (2.2) решение в виде ряда, умножаем на величину 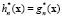 , (
, (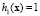 ), и интегрируем по пространству, получаем уравнения
), и интегрируем по пространству, получаем уравнения
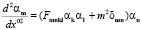 . (2.3)
. (2.3)
Определим координаты положения равновесия для этой системы нелинейных уравнений. Эта система нелинейных уравнений разбивается на линейное уравнение, из которого переменная n определится с точностью до множителя из линейного уравнения
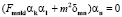 .
.
Для того чтобы эта система имела решение, определитель этой системы уравнений должен быть нулевой
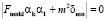 . (2.4)
. (2.4)
Тогда имеем первое приближение 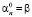 . Откуда из равенства нулю определителя определяем комплексную константу , где величина n в общем случае комплексная. Подставляем в матрицу уравнения (2.4) комплексное значение
. Откуда из равенства нулю определителя определяем комплексную константу , где величина n в общем случае комплексная. Подставляем в матрицу уравнения (2.4) комплексное значение 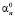 и из линейного уравнения определяем
и из линейного уравнения определяем 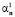 с точностью до множителя, который определяем подстановкой в определитель (2.4). В результате итераций получаем конечную совокупность (при бесконечном числе членов ряда счетную) количества комплексных в общем случае решений.
с точностью до множителя, который определяем подстановкой в определитель (2.4). В результате итераций получаем конечную совокупность (при бесконечном числе членов ряда счетную) количества комплексных в общем случае решений.
При этом координаты положения равновесия не устойчивы, так как решение линеаризованной системы уравнений 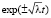 . Это приводит к бесконечности решения в случае действительного решения (см. [4]). И к чередованию приближения к координате положения равновесия в случае комплексного решения (см. [4]). Т.е. на интервале времени, характерном для квантового описания системы, имеется множество приближений к координатам положения равновесия, но измерение квантовой механики реализует одно из них. Но определяемые этими координатами положения равновесия собственные значения квантовой системы устойчивы. В результате измерения квантовой системы получается одно собственное значение.
. Это приводит к бесконечности решения в случае действительного решения (см. [4]). И к чередованию приближения к координате положения равновесия в случае комплексного решения (см. [4]). Т.е. на интервале времени, характерном для квантового описания системы, имеется множество приближений к координатам положения равновесия, но измерение квантовой механики реализует одно из них. Но определяемые этими координатами положения равновесия собственные значения квантовой системы устойчивы. В результате измерения квантовой системы получается одно собственное значение.
При этом, так как дифференциальное уравнение (2.3), полученное из уравнения движения (2.2), имеет в общем случае комплексные координаты положения равновесия, ее действительное решение согласно теореме 1 см. [4] стремится к бесконечности и как это описано в литературе является обобщенной функцией. При этом комплексное решение этого нелинейного уравнения конечно согласно теореме 2 см. [4], и сводится к чередованию приближения к координатам положения равновесия.
Можно прибегнуть к другому способу вычисления собственных значений, рассматривая решение двух уравнений
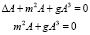 (2.5)
(2.5)
Решение ищем в комплексном пространстве в виде
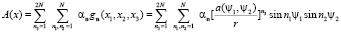 . (2.6)
. (2.6)
Где величины углов равны
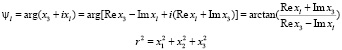
Подставляем формулу (2.6) в дифференциальное уравнение (2.5), умножаем уравнение на величину 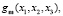
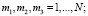
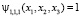 , и интегрируем по комплексному пространству, получим систему 2N3 уравнений с 2N3 неизвестными.
, и интегрируем по комплексному пространству, получим систему 2N3 уравнений с 2N3 неизвестными.
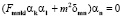 .
.
Решение с помощью функций (2.6) сходится лучше, чем с помощью сферических функций. Сферическая система координат не периодичная, угол 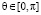 , и поэтому коэффициенты ряда по сферическим функциям на бесконечности индекса стремятся к бесконечности. Так разложение плоской волны по сферическим функциям, имеет вид
, и поэтому коэффициенты ряда по сферическим функциям на бесконечности индекса стремятся к бесконечности. Так разложение плоской волны по сферическим функциям, имеет вид
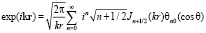
Где сферические функции 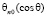 ортонормированны.
ортонормированны.
При этом коэффициенты ряда Фурье в случае непрерывной функции сходятся на бесконечности индекса быстрее чем 1/n2. Т.е. второе решение сходится лучше, чем решение со сферическими функциями. Причем нулевое приближение для коэффициентов, можно брать в виде
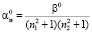 ,
,
а следующее приближение в виде
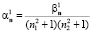 ,
,
что ускорит процесс сходимости определения коэффициентов.
Отметим, что функциональный интеграл можно вычислить методом перевала. При этом критическая точка, или точка перевала функционального интеграла равна функции
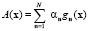
и не зависит от времени, т.е. функциональный интеграл можно проинтегрировать по времени в критической точке. Причем критических точек имеется счетное количество, как и количество собственных значений оператора энергии. При этом возникнет большой параметр, равный приращению времени и интеграл можно считать методом перевала, причем фаза и амплитуда метода перевала определится в виде конечного интеграла.
Запишем выражение, определяющее собственную энергию частицы
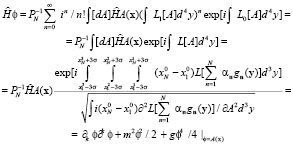
Где величина
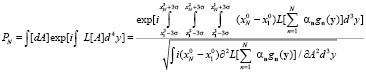 .
.
Так подынтегральное выражение в фазе экспоненты не зависит от времени, по времени можно проинтегрировать, и получим большой параметр 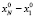 .
.
Где величина классической функции плотности Лагранжа равна
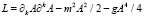 ,
,
а функция плотности Гамильтона равна
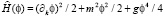 .
.
Причем значение A(x) не зависит от времени в точке координаты положения равновесия. При этом значение величины A надо брать из формулы
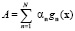 .
.
Фаза и амплитуда формулы метода перевала считается с помощью континуального интеграла. При этом имеется точка метода перевала
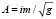 ,
,
в которой
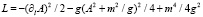 .
.
Используя точку метода перевала
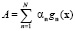 ,
,
причем в точке перевала 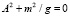 получим
получим
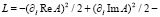
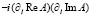 .
.
Выбираем контур, удовлетворяющий
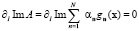 ,
,
получаем зависимость
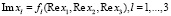
и интегрируем по действительной переменной, используя вычисленные мнимые значения переменных, для нахождения фазы интеграла. При этом используется метод стационарной фазы, так как функция Лагранжа умножается на мнимую единицу.
Причем точек перевала имеется счетное количество, но энергия состояния определяется по единой формуле для любой одной точки метода перевала. Одна точка метода перевала определяет одну совокупность координат положения равновесия и одно значение энергии состояния. Плотность энергии равна
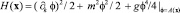 ,
,
где энергия берется при квантовом поле равном классическому полю, полученному с помощью метода Галеркина. Количество собственных значений энергии определяется числом совокупностей положения равновесия системы (2.2).
При этом в случае вычисления скалярного поля имеем для него конечное значение
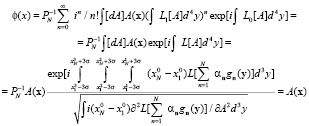
Получаем, что квантовое поле равно классическому полю
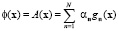
и, следовательно, комплексная энергия этого поля равна 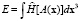 , причем количество собственных энергий равно количеству совокупностей координат положения равновесия, т.е. при бесконечном числе членов ряда имеется счетное количество собственных значений энергии.
, причем количество собственных энергий равно количеству совокупностей координат положения равновесия, т.е. при бесконечном числе членов ряда имеется счетное количество собственных значений энергии.
Преобразование Лоренца в комплексном пространстве
В комплексном пространстве метрический интервал будет комплексный
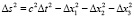 .
.
При этом преобразование Лоренца запишется в виде
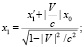
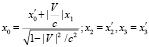
Где величины координат комплексные. При не релятивистских скоростях пространство комплексно, а время действительно. Причем в этом случае комплексное пространство ограничено, и расположено около поверхности тел, а вдали от тел пространство действительно. Причем модуль пространственной части много меньше 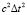 в случае не релятивистских скоростей. При релятивистских скоростях время и пространство комплексно, и не ограничено.
в случае не релятивистских скоростей. При релятивистских скоростях время и пространство комплексно, и не ограничено.
Оператор момента импульса в комплексном пространстве
Отметим, что квантовые числа L, M, s, операторов спина могут иметь не целое значение и быть комплексные. При этом собственное значение волновой функции 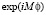 определяется по формуле
определяется по формуле
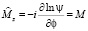
всегда целые. При этом вводится величина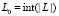 и величины
и величины
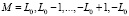 ,
,
причем имеется 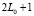 значений проекций момента импульса. Причем величина орбитального момента L может быть комплексной. Тогда, как предложено и обоснованно в [5] энергия возбуждения атома водорода комплексная и равна
значений проекций момента импульса. Причем величина орбитального момента L может быть комплексной. Тогда, как предложено и обоснованно в [5] энергия возбуждения атома водорода комплексная и равна
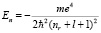 ,
,
где орбитальный момент l комплексный. При этом углы сферической системы координат в комплексном пространстве действительны, а радиус комплексный
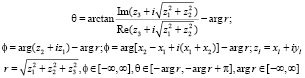 .
.
Где справедливо
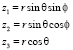
Выводы
Комплексное решение, которое существует в случае комплексных координат положения равновесия, назовем турбулентным, в силу физического смысла комплексного решения в макропространстве, причем в [6] описаны мнимые параметры макромира. Мнимая часть комплексного решения описывает отклонение от среднего решения, и определяет вращающуюся или осциллирующую часть решения. Причем возможно особое комплексное решение при определенных значениях энергии системы, т.е. дисперсия решения, может проявиться и быть не нулевой при определенных значениях энергии или импульса. Расчеты в комплексном пространстве нелинейных уравнений в частных производных являются непрерывными функциями, а не обобщенными функциями, не стремятся к бесконечности, и не требуют перенормировок.

