1. Кинетика формирования центров кристаллизации на потенциальных зародышах.
Термодинамическим путем, исходя из теории зарождения новой фазы Гиббса-Фольмера, выведено кинетическое уравнение образования центров кристаллизации, обусловленногоприсутствием потенциальных зародышей:
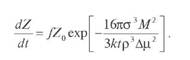(1)
где Z - концентрация зародышей, м-3, определяемая как отношение числа зародышей
кристаллов к объему системы; t - время, с; b - кинетический коэффициент, м-3-с-1; к - постоянная Больцмана, Дж/К.
В качестве движущей силы рассматривается разность электрохимических потенциалов:
μ э= μ + zFE (2)
где z - заряд иона; F - постоянная Фарадея, Кл/моль; Е - разность электрических потенциалов, В; ц - химический потенциал.
Термодинамическая способность системы к зарождению новой фазы характеризуется отношением
(3)
где rкр - критический радиус зародышей кристалла.
Значения этого отношения по порядку величины характерно для зарождения центров кристаллизации по гетерогенному механизму на потенциальных зародышах.
Чем меньше это отношение, тем выше скорость зарождения кристаллов, согласно уравнению (1). Ввиду своей сложности последнее апроксимируется формулой:
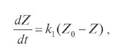(4)
где 
- коэффициент скорости зарождения центров кристаллизации, с-1.
Для изотермического псевдостационарного процесса (Т,σ,Δμ = const):
(5)
из которого следует, что скорость процесса убывает со временем от значения k1Z0 до нуля.
Объем частицы новой фазы, возникшей в момент времени т, к моменту t достигает значения:
(6)
где фV - объемный фактор формы кристалла, который учитывает форму кристалла и способ измерения величины k, м/c
Относительный объем всех частиц можно выразить следующим интегральным уравнением типа свертки:
Подставляя в уравнение (7) скорость зарождения центров кристаллизации из (5), получим формулу для вычисления относительного объема новой фазы в изотермическом псевдостационарном процессе:
(8)
Аналогично выводятся уравнения для расчета относительной площади поверхности новой фазы А: в изотермическом псевдостационарном процессе:
(9)
и в общем случае:
(10)
Где фа - поверхностный фактор формы кристалла (для сферической частицы равный п); Z´0, Z´ - поверхностная плотность потенциальных зародышей и возникших центров кристаллизации, м2
2. Механизм формирования новых центров на первичных зародышах.
Скорость вторичного зарождения центров кристаллизации пропорциональна площади поверхности образовавшейся новой фазы:
где k2 =k2 (T,σ,Δμ) - коэффициент скорости вторичного образования центров кристаллизации, м-2-с-1
Тогда при подстановке уравнения (9) в (11) получим:
(12)
Общая скорость зарождения центров кристаллизации по первичному и вторичному механизмам определится суммой уравнений (6) и (12):
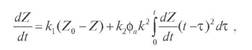
Решение относительно dZ/dt этого интегрального уравнения имеет вид
где 
Зарождение кристаллов на первичных зародышах должно приводить к образованию дендритных фаз боридов, что в условиях электролизного борирования железа не наблюдалось.
3. Выразим скорость зарождения центров кристаллизации с учетом захвата потенциальных зародышей уравнением:
При подстановке (16) в (7) и (9) получены интегральные уравнения, решение которых с применением преобразования Лапласа дает формулы для расчета V и A:
где:
Объёмная и поверхностная характеристические константы легко определяются на основе времени полного заполнения поверхностного слоя зародышами кристаллов борида т, с. по экспериментально определенному значению времени заполнения т может быть вычислена характерная константа
При электролизном борировании железа экспериментальное значение времени полного заполнения поверхности железа зародышами борида составляет 180 с, поэтому объемная и характеристические константы, вычисленные по формулам (17) и (18), равны: α = 8,7267Т0-3 с-1; α´ = 0,010277-с-1.