Пусть материальная частица располагается на винтовой поверхности спирали, установленной в насыпи и вращающейся относительно оси с угловой скоростью. При движении частица прижимается к внешним слоям и к витку спирали. Нахождение скорости, обуславливающей производительность, связано с определением угловой скорости относительного движения ' при соблюдении условия равновесии из решения системы уравнений [1]:
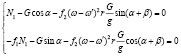 , (1)
, (1)
где G – вертикальная составляющая силы давления частицы на спираль; r – радиус спирали; N2 – сила, соответствующая давлению насыпи на материальную частицу; N1 – давление поверхности спирали; f1 – коэффициент трения о виток спирали; f2 – коэффициент трения о насыпь.
Умножим первое уравнение системы (1) на f1, и сложим его со вторым, сокращая на G получим:
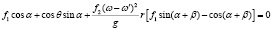 . (2)
. (2)
Положив в уравнении (2) = 0°, cos = 1, sin = 0, условия, при которых подъема частицы не будет, имеем:
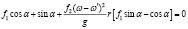 . (3)
. (3)
Отсюда 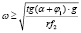 ,
,
где 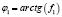 .
.
Следовательно, для движения массы частиц вверх вдоль оси спирали необходимо соблюдение данного условия.

