Задачи на построение в пространстве решаются двумя принципиально различными методами: в воображении и на проекционном чертеже.
В процессе решения задачи на построение в воображении устанавливается лишь факт существования решения, само же построение искомого элемента не выполняется. Решение задачи сводится к перечислению такой совокупности геометрических операций, фактическое выполнение которых приводит к построению искомого элемента. Рисунок, который сопровождает воображаемые (условные) построения, носит исключительно иллюстративный характер.
При решении задач на построение на проекционном чертеже с помощью определенного набора инструментов (обычно, как и в планиметрии, это циркуль и линейка) явно выполняется конечная последовательность построений, приводящая к искомому элементу.
Специфика задач на построение в пространстве состоит в том, что не существует чертежных инструментов, позволяющих чертить геометрические фигуры непосредственно в пространстве. Пространственные фигуры изображаются плоским рисунком, а значит, такой рисунок во многом является условным: линейные и угловые размеры на нем искажаются.
В школьном курсе стереометрии учащимся предлагаются задачи, как на воображаемые построения, так и на построение на проекционном чертеже.
В данной статье рассматриваются задачи на позиционно полных изображениях.
В геометрии изображение фигуры на плоскости получается в результате параллельного или центрального проектирования. Поэтому изображение (чертеж) называют проекционным чертежом.
С центральным проектированием связан метод линейной перспективы, в котором получается наглядное изображение фигуры. Это объясняется тем, что глаз человека работает по принципу линейной перспективы.
С параллельным проектированием связаны, например, такие методы:
а) метод произвольной параллельной проекции или просто метод параллельной проекции;
б) метод Монжа;
в) метод аксонометрии и др.
Перейдем к вопросу о параллельном проектировании и его свойствах.
Различают ортогональное и кабинетное параллельное проектирование.
В зависимости от цели используются изображения следующих трех видов: иллюстративные, полные, метрически определенные. Ко всем этим изображениям предъявляются такие требования: изображение должно быть верным, то есть оно должно представлять собой фигуру, подобную произвольной параллельной проекции; изображение должно быть по возможности наглядным, то есть должно вызывать верные пространственные представления об изображаемой фигуре; изображение должно быть легко выполнимым, то есть правила построения должны быть максимально простыми; изображение должно быть удобоизмеримым, то есть по изображению можно, и притом несложно, восстановить оригинал метрически точно.
Для учащихся в курсе стереометрии новым понятие является понятие скрещивающиеся прямые. Как показывает анализ практики, школьникам трудно даются такие понятия как общий перпендикуляр двух скрещивающихся прямых, угол между скрещивающимися прямыми, параллельные плоскости, проходящие через две скрещивающиеся прямые и т.д.
Как показал наш опыт, задачи, приведенные ниже, помогут учащимся глубже и сознательнее усвоить перечисленные выше понятия.
Задача 1. Провести прямую, параллельную данной прямой и пересекающую каждую из двух данных скрещивающихся прямых.
Задача 2. Расстояние между двумя взаимно перпендикулярными скрещивающимися прямыми равно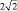 
. Провести прямую, пересекающую эти прямые и образующую с каждой из них угол в 60°.
Задача 3. На одной из двух данных скрещивающихся прямых найти точку, равноудаленную от другой прямой и от данной точки пространства, не принадлежащей этим прямым.
Задача 4. Через одну из двух данных скрещивающихся прямых провести плоскость, параллельную другой прямой.
Задача 5. Через каждую из двух скрещивающихся прямых провести плоскости так, чтобы эти плоскости были бы параллельными между собой.
Задача 6. Через данную точку M провести прямую, перпендикулярную каждой из двух данных скрещивающихся прямых a и b.
Задача 7. Провести прямую, пересекающую две данные скрещивающиеся прямые a и b и проходящую через точку M, не принадлежащую прямым a и b.
Задача 8. Дан куб ABCDA1B1C1D1. Через середину ребра AA1 построить прямую, пересекающую прямые D1C1 и BC.
Перейдем к разговору о построении сечений многогранников.
Наиболее доступными и эффективными в практике преподавания геометрии в школе являются следующие три метода построения сечений многогранников: метод следов; метод соответствия или внутреннего проецирования (иногда его называют методом вспомогательных сечений); комбинированный метод.
Построения сечений многогранников, которые проводятся в школе, основываются на следующей теореме.
Теорема. Если изображение любого многогранника полное, то на изображении можно построить его сечение, заданное тремя точками.
Обращаем внимание читателя еще на то, что неотъемлемой частью процесса решения позиционных задач на построение сечений геометрических фигур, является необходимость определения видимых и невидимых контуров соответствующих построений.
Выполнение такого требования, полезно хотя бы потому, что оно:
1) обеспечивает наглядное оформление решения позиционной задачи, а значит, обеспечивает быстрое и безошибочное чтение этого решения;
2) содействует развитию пространственных представлений и пространственного воображения учащихся;
3) содействует подготовке учащихся к восприятию таких курсов, как начертательная геометрия и техническое черчение (во втузе).
Рассмотрим вопрос о сечении геометрических тел методом следов.
Приступая к решению таких задач, рекомендуем обратить особое внимание на осмысливание того, что значит построить сечение многогранника или тела вращения плоскостью и в чем состоит сущность метода следов.
1. Построить сечение многогранника (тела вращения) плоскостью – это значит построить прямые (кривые), являющиеся следами на гранях многогранника (поверхности тела вращения) заданной плоскости.
В сечении многогранника всегда получим многоугольник, вершины которого расположены на ребрах многогранника; в сечении тела вращения – плоскую фигуру, ограниченную замкнутой кривой линией (например, эллипс), но может получиться и плоская фигура – комбинированная линия, состоящая из чисто кривой и отрезка прямой.
В сечении многогранника можно получить треугольник, четырехугольник и т.д. Число сторон сечения равно количеству граней данного многогранника.
2. Метод следов состоит в том, что на плоскости нижнего основания многогранника, цилиндра или на плоскости основания конуса выполняется построение следов (линий и точек пересечения секущей плоскости с некоторыми прямыми и плоскостями). С помощью этих следов легко выполняется построение точек пересечения секущей плоскости с ребрами многогранников (с образующими тела вращения) и линий пересечения плоскости с гранями многогранника (с поверхностью тела вращения).
Обстоятельный разговор об обучении учащихся решению планиметрических и стереометрических задач на построение читатель найдет в наших работах [2, 3] .