В атмосферу поступает множество вредных веществ. Помимо нарушений функционирования различных систем организма, хронических заболеваний внутренних органов, некоторые вещества представляют опасность как канцерогены. В отличие от других факторов, влияющих на состояние здоровья, воздействие продуктов антропогенных выбросов на человека отрегулировать невозможно. В связи с тем, что последствия такого воздействия могут реализовываться спустя годы и десятилетия, актуальной задачей становится долгосрочный прогноз риска r онкологических заболеваний населения вследствие воздействия канцерогенных веществ, содержащихся в выхлопных газах автомобилей и выбросах предприятий. Задача долгосрочного гидродинамического прогноза параметров атмосферы является исключительно сложной, что обусловлено рядом причин. Разработанный методический подход, применим для долгосрочного прогноза канцерогенного риска для районов г. Алматы, Шымкента, Тараза и для других мегаполисов. Численные эксперименты проведены для микрорайона 3, 4, 5, 6, 7, 8, 9, 10.
В атмосферу поступает множество вредных веществ, например, бенз(а)пирен, сажа, свинец, пары бензина, медь и другие. Помимо нарушений функционирования различных систем организма, хронических заболеваний внутренних органов некоторые вещества представляют опасность как канцерогены. В отличие от других факторов, влияющих на состояние здоровья, воздействие продуктов антропогенных выбросов на человека отрегулировать невозможно. В связи с тем, что последствия такого воздействия могут реализовываться спустя годы и десятилетия, актуальной задачей становится долгосрочный прогноз риска r онкологических заболеваний населения вследствие воздействия канцерогенных веществ, содержащихся в выхлопных газах автомобилей и выбросах предприятий.
В выражении
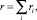(1)
здесь ri = ri (qi (Y), Y) – зависимость рисков от концентрации канцерогенных веществ в детерминированном виде отсутствует. Известны только эмпирико-статистические зависимости типа уравнения регрессии, установленные на основе исследования чувствительности величины ri от вариаций qi. Помимо этого, задача долгосрочного гидродинамического прогноза параметров атмосферы является исключительно сложной, что обусловлено рядом причин, среди которых главными является быстрое ухудшение значимости решения с увеличением заблаговременности и большая трудоемкость получения оценок реакции атмосферы на различные внешние воздействия с помощью существующих методов численного прогноза. Как правило, эти возмущения малы по сравнению с невозмущенными значениями и оценка их влияния может искажаться фиктивными шумами, порождаемыми самой численной моделью.
В связи с этими обстоятельствами представляется перспективным применение методов теории чувствительности [2] к постановке и решению задачи долгосрочного прогноза риска r. Введем термины: вектор состояния и вектор параметров. Под вектором состояния понимается вектор, составляющими которого являются риски ri обусловленные различными канцерогенными примесями qi. Под вектором параметров в данном случае понимается вектор Y (вектор параметров атмосферы и параметров источника).
Введем в рассмотрение функции чувствительности:
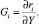(2)
Функции чувствительности представляют собой изменения вектора состояния, соответствующие единичным изменениям составляющих вектора параметров, т.е. частные производные от решений уравнений (1) по составляющим вектора параметров в окрестности невозмущенных решений. Процесс расчета рисков ri, при этом становится предельно простым и состоит в перемножении вариаций параметров модели и заранее рассчитанных функций чувствительности.
С учетом вида выражения (1) преобразуем правую часть соотношения (2)
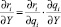
и функции чувствительности (2) представим в виде
Gi = Ri•Qi, (3)
где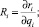 
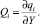
Функции чувствительности Ri рассчитаны и приведены в работе [3] посвященной оценке канцерогенных рисков, обусловленных загрязнением воздуха транспортными потоками в 3ападном районе города Тараз, Алматы.
Для расчета полей функций чувствительности Qi целесообразно использовать уравнения, описывающие задачу долгосрочного прогноза полей канцерогенных примесей, в вариациях [4]. С этой целью используются представления векторов состояния и параметров в виде суммы невозмущенных значений (qio, Yo) и малых возмущений (δqi, δY).
qi = qio + η•δqi; Y = Yo + η•δY,
где η – вещественный параметр.
Если записать структуру модели в виде операторного уравнения
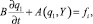(4)
то уравнения в вариациях представляются в виде
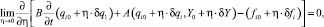(5)
где В – диагональная матрица; А (qi, Y) – нелинейный матричный дифференциальный оператор.
В основу модели расчета полей функций чувствительности Qi положено уравнение эволюции примесей. Ниже приведен общий вид данного уравнения:
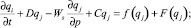WS = –gρVS. (6)
Далее уравнение эволюции примесей представлено в вариациях:
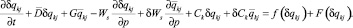(7)
Для численной реализации модели расчета полей функций чувствительности Qi используется выражение, которое демонстрирует частный случай уравнения эволюции примесей:
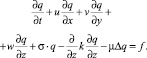(8)
Данное уравнение справедливо для легких примесей. В вариациях оно выглядит следующим образом:
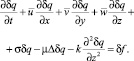(9)
Полученные таким образом уравнения в вариациях при фиксированных невозмущенных значениях составляющих вектора состояния линейны. В виду этого обстоятельства представляется возможность, не прибегая к моделированию основного (невозмущенного) состояния, оценивать его вариации на больших масштабах времени, вплоть до климатических.
Для вычисления функций чувствительности к вариациям компоненты Yk осуществляется интегрирование по времени уравнений в вариациях, в котором эта компонента вектора параметров полагается равной единице, остальные – нулю. Полученные таким образом решения представляют собой трехмерные поля функций чувствительности к единичным вариациям конкретного параметра на временном интервале (равном интервалу интегрирования уравнений в вариациях) и позволяют количественно оценивать изменения составляющих вектора состояния (Δqi), соответствующих заданному полю вариаций параметров (ΔY):
Δqi = Qi ΔY.
С учетом соотношений (2), (3) отсюда следует выражение для расчета рисков
Δri = Gi ΔY = Ri Qi ΔY. (10)
Подтверждением работоспособности предложенного подхода стало разумное соответствие результатов выполненных численных экспериментов результатам, опубликованным в других работах.
Численные эксперименты по прогнозу канцерогенного риска проведены для микрорайона 3, 4, 6, 7, 8, 9, 10 г. Тараз для самого жаркого и самого холодного месяца года (июль и январь соответственно). В эксперименте участвовали лишь выбросы от автотранспорта. Полученные прогнозируемые уровни канцерогенного риска для указанного микрорайона довольно низкие, что говорит о незначительном вкладе автомобильного транспорта в общее количество онкологических заболеваний.
Прогноз риска может осуществляться с учетом меняющихся условий среды и параметров источника выбросов вредных веществ. Разработанный методический подход применим для долгосрочного прогноза канцерогенного риска для других районов г. Алматы Шымкента, Тараза и других мегаполисов. Результаты могут служить основой принятия необходимых управленческих решений, направленных на минимизацию риска.
С другой стороны при выборе подходящей математической модели процесса распространения газообразных примесей в атмосфере необходимо учитывать, что он объединяет в себе такие различные процессы как перенос ветром, турбулентная диффузия, поглощение и химические превращение примесей. В общем процессе распространиения примесей можно описать следующей дифференциальной моделью в частных производных:
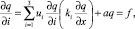(11)
где q(x, t) – определенная концентрация примесей в точке (x = x1, х2, х3) в момент времени t,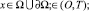 
u = (u1, u2, u3) – вектор скорости ветра с составляющими вдоль осей координат x1, х2, х3; k1, k2, k3 – коэффициент турбулентной диффузии вдоль соответсвующих осей координант; а – коэффициент интенсивности поглащения примесей атмосферой; f(x, t) – обобщенная функия, характеризирующая источники выбросов на местности.
В случае наличия нескольких точечных источников функия f(x, t) – апроксимируется следующим выражением
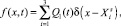
где Q1(t) мощность выброса источника Is. Если источник является постоянно действующим (типичным пример – трубы ТЭЦ), можно представить в виде const. Для случаев аварийнных выбросов такое представление, по-видимому, неприемлемо. Здесь, в зависимости от характера аварии, можно остановится на одном из следующих трех вариянтов:
1) экспоненциальный режим
Q(t) = M0exp(–at),
где M0 – начальный выброс; а – коэффициент интенсивности выброса;
2) последущее стационирование выброса
Q(t) = Mmfx[1 – exp(–at)],
где Mmfx – максимальная мощность выброса;
3) колебательный режим
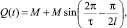
где М – амплитуда выброса.
Если обратится к модели распространения, можно констатировать, что у нас нет надежды получить в общем виде аналитическое решение уравнения (11), то почему бы сразу не приступить к его численному решению на ЭВМ. Причина невозможности этого кроется в самой природе турбулентного потока. Решить задачу прогноза распространения, по видимому, можно только путем разработки достаточно простого и эффективного требования, которое связано с прогнозированием, очень важно не пропустить опасные уровни загрянения, пусть даже это иногда будет приводить к ложной тревоге.