Scientific journal

International Journal of Experimental Education

ISSN 2618–7159

ИФ РИНЦ = 0,425

(1)

где λ - спектральный параметр, функция ρ(х) называется весовой функцией, функция q(x) называется потенциалом.

Для изучения асимптотики собственных значений и собственных функций краевых задач, связанных с дифференциальным уравнением (1), необходимо знать асимптотику решений дифференциального уравнения (1).

Пусть - некоторая фиксированная ветвь корня, выбранная условием 3√1 = +1. Пусть ω_к - корни третьей степени из единицы, то есть

Эти числа удовлетворяют следующим свойствам: 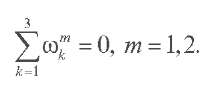Будем предполагать, что ρ(x) € C³ [0;π]. Потенциал q(x) - суммируемая функция:

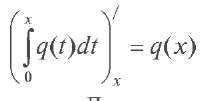почти всюду на отрезке 0;п ] .(2)

Для нахождения асимптотики решений дифференциального уравнения (1) при выполнении условия гладкости (2) сначала рассмотрим вспомогательное уравнение

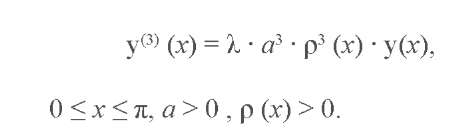 (3)

Теорема 1. Общее решение дифференциального уравнения (3) имеет следующий вид:

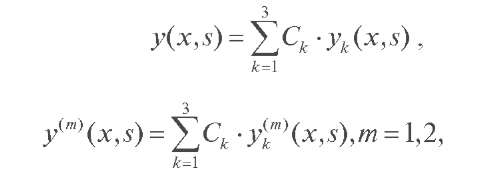 (4)

где C_k (k = 1, 2, 3) - произвольные постоянные, y_k (x, s) - линейно независимые решения дифференциального уравнения (3), причём при |s|→+∞ справедливы следующие асимптотические разложения 

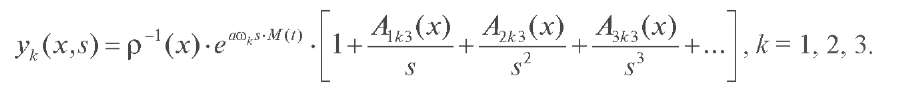
Идею разложения вида (5) мы нашли в монографии М.В. Федорюка [1].

В формуле (5) введено следующее обозначение

Продифференцируем асимптотические разложения вида (5) почленно три раза, для этого достаточно выполнения условия гладкости р(х) € C³ [0; п], и подставим получившиеся формулы в дифференциальное уравнение (3), приведём подобные слагаемые и приравняем коэффициенты при одинаковых степенях s (этот метод называется методом последовательных приближений Хорна). При этом найдём в явном виде коэффициенты А_1k3(х), A_2k3(x), .... Это не было сделано ни в монографии [1], ни в других работах

Впервые это было сделано автором (для аналогичного уравнения второго порядка) в §3 главы монографии [2]. Автором разработан метод нахождения асимптотики собственных значений и асимптотики собственных функций краевых задач при условии выполнения (2). Для случая n = 2, p(x) = 1 другой метод был продемонстрирован в работе [3]. Для дифференциального оператора второго порядка с непостоянной весовой функцией это было проделано автором в работе [4]. Приведём явные формулы, полученные нами.

Введём необходимые нам обозначения

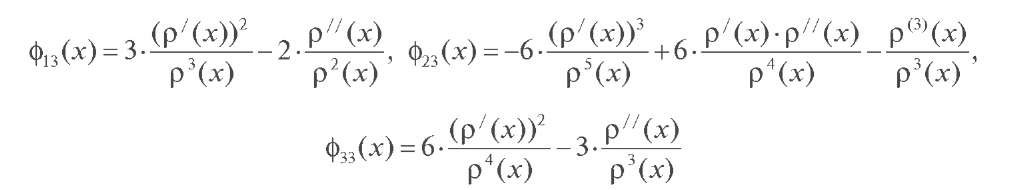
Тогда справедливы следующие формулы:

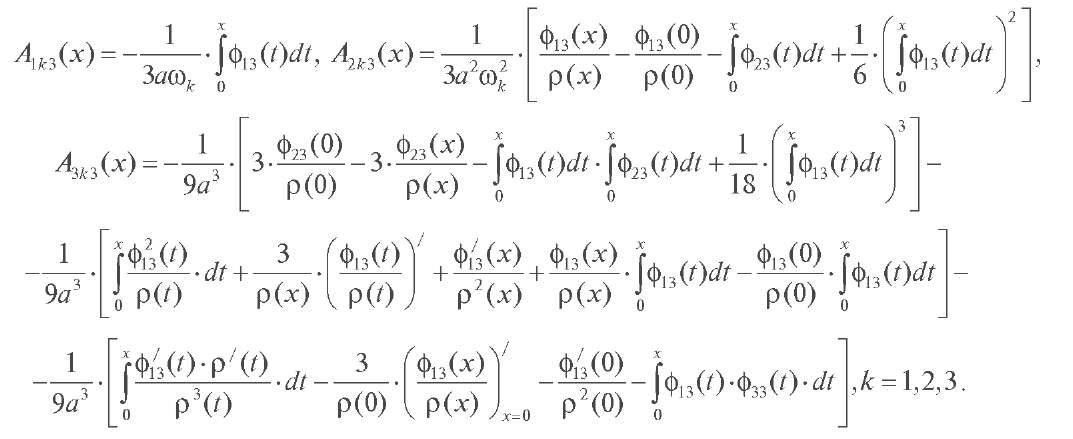
Аналогичные формулы справедливы также для функций y_k^/[(x,s) и y_k^//(x,s), k = 1, 2, 3. В результате получаем

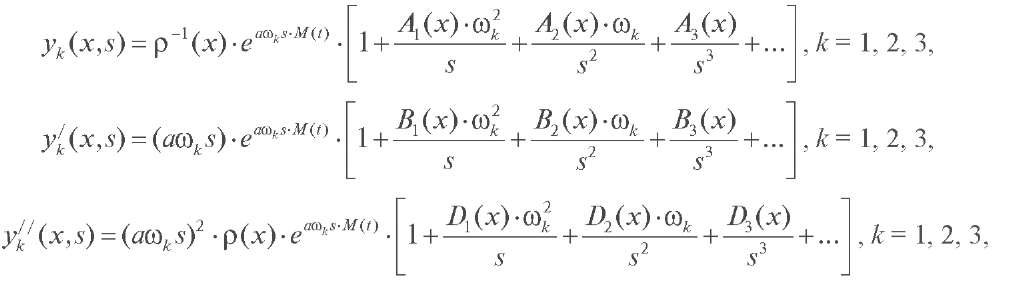
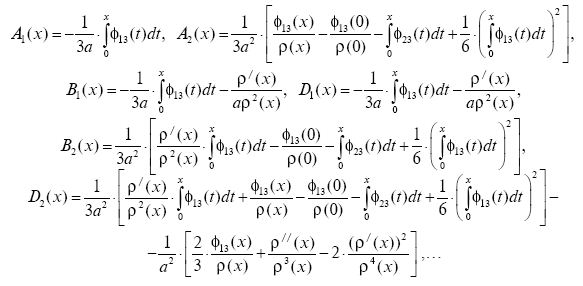
Теорема 2. Определитель Вронского

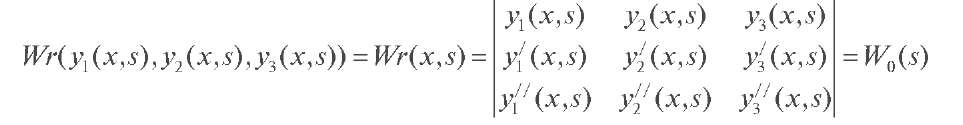
линейно независимых решений y1 (x, s), y2 (x, s), y3 (x, s) дифференциального уравнения (3) не зависит от переменной x и имеет следующую асимптотику:

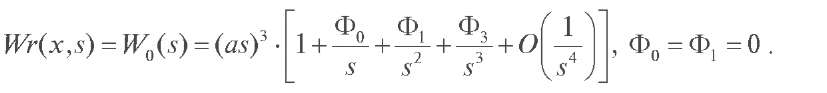
Доказательство теоремы 2 можно осуществить двумя способами. Первый заключается в подстановке асимптотик (8)-(11) в формулу (12) и разложении определителя по столбцам. При этом можно показать, что

При этом получаем

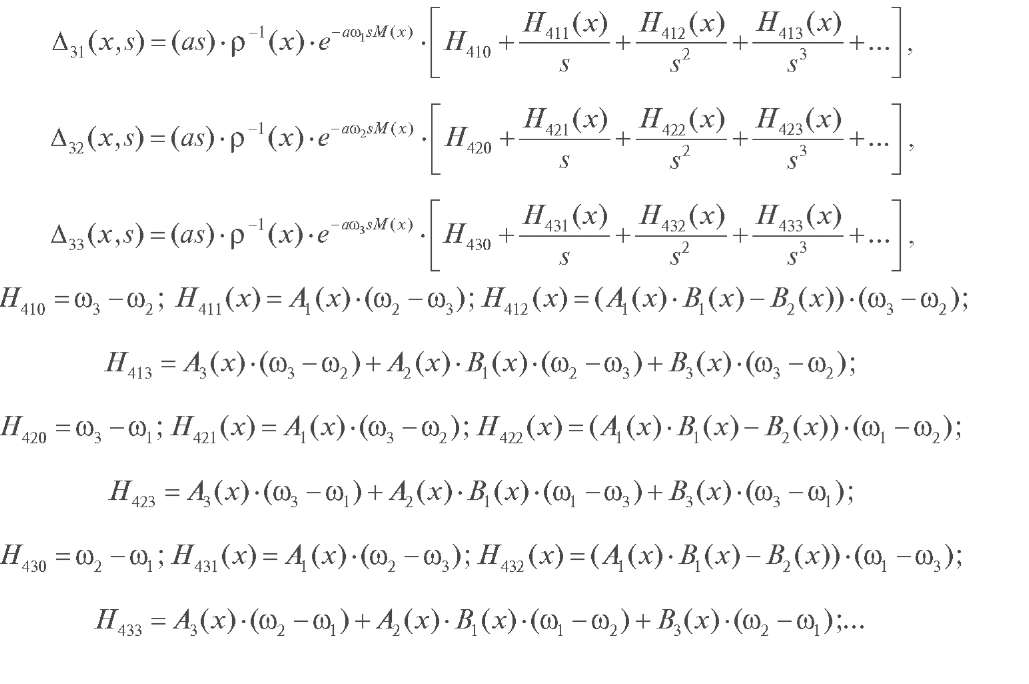
Перейдём к нахождению асимптотики решений дифференциального уравнения (1). Общее решение дифференциального уравнения (1) будем искать методом вариации постоянных в следующем виде:

где y1 (x, s), y2 (x, s), y3 (x, s) - линейно независимые решения вспомогательного дифференциального уравнения (3), C1 (x, s), C2 (x, s), C3 (x, s) - неизвестные функции, которые можно найти из следующей системы уравнений:

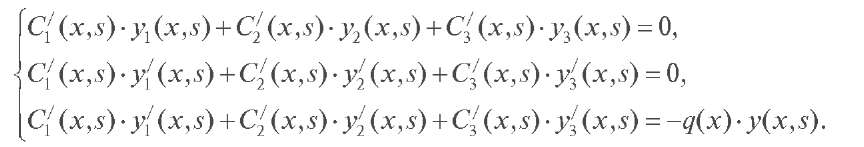
Решая систему (20), приходим к выводу, что справедливо следующее утверждение.

Теорема 3. Решение y (x, s) дифференциального уравнения (1) является решением следующего интегрального уравнения Вольтерра:

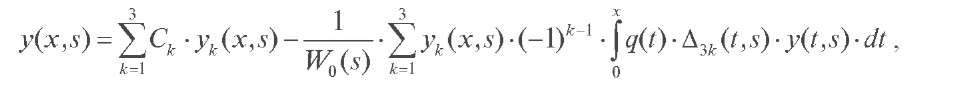
где yk (x, s) (k = 1, 2, 3) - линейно независимые решения дифференциального уравнения (3), асимптотика которых определена формулами (4)-(11), W0 (s) - определитель Вронского этих решений (см. (12), (13)).

Далее применим метод последовательных приближений Пикара: найдём y (t, s) из (21) и снова подставим его в уравнение (21).

Теорема 4. Общее решение уравнения (1) имеет следующий вид:

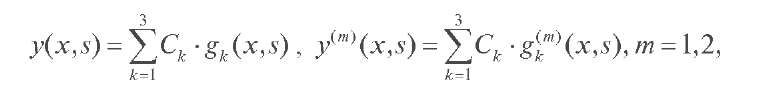
где Ck (x, s) (k = 1, 2, 3) - произвольные постоянные, gk (x, s) - линейно независимые решения дифференциального уравнения (1), причём при |s|→+∞ справедливы следующие асимптотические разложения:

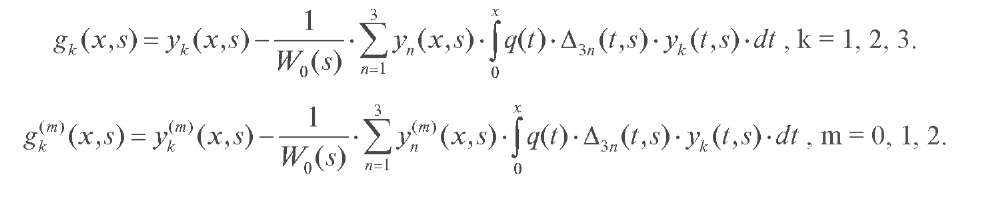
Список литературы:

1. Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. - М.: Наука, 1983. - 352с.
2. Митрохин С.И. Спектральная теория операторов: гладкие, разрывные, суммируемые коэффициенты. М.: ИНТУИТ, 2009. - 364 с.
3. Винокуров В.А., Садовничий В.А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма-Лиувилля на отрезке с суммируемым потенциалом // Известия РАН. Серия: матем. -2000. - Т. 64, № 4. - С. 47-108.
4. Митрохин С.И. Асимптотика собственных значений краевой задачи Штурма-Лиувилля с суммируемым потенциалом и гладкой весовой функцией. - 2008. - Рукопись депонирована в ВИНИТИ 07.07.2008, №581-В2008.