Дифференциальные уравнения (ДУ) имеют большое прикладное значение. Они выступают универсальным средством исследования многих технических и технологических задач. Применение ДУ в различных сферах связано с тем, что закономерности многих явлений и процессов эффективно описываются ими. Дисциплина «Математика» для технических направлений подготовки на уровне бакалавриата обязательно включает раздел математического анализа, который знакомит студентов первых курсов с основными видами ДУ. Знакомству с ДУ предшествуют темы, раскрывающие содержание дифференциального и интегрального исчислений. Основная задача изучения ДУ – это формирование системы знаний и умений, которая позволит студентам успешно осваивать методы математического моделирования на занятиях по специальным дисциплинам на старших курсах бакалавриата и на второй ступени вузовского образования в магистратуре.
Изучение ДУ в рамках дисциплины «Математика» осуществляется по схеме: определение > общее и частное решение > ДУ первого порядка > ДУ высших порядков [4, 7]. Освоение способов решения ДУ вызывает определенные затруднения у студентов. Это объясняется тем, что различные типы ДУ решаются разными методами, поэтому очень важно правильно определять тип ДУ. Если выбор будет ошибочным, то затраченные усилия не позволят получить верный результат и приведут к потере познавательного интереса. Овладение способами решения ДУ первого порядка основных типов (уравнение с разделяющимися переменными, однородное и линейное неоднородное) обеспечивает студентам более успешное освоение методов нахождения общего и частного решений ДУ других типов. Уделяя должное внимание на начальном этапе изучения этого раздела формированию умений анализировать процесс решения ДУ, можно рассчитывать на повышение эффективности деятельности студентов при изучении ДУ второго и третьего порядков.
Результаты исследования и их обсуждение. Продуктивной представляется методическая идея об изучение типов ДУ с использованием задач с геометрическим содержанием для их составления. Выбираются такие задания, выполнение которых требует от студентов актуализации знаний, полученных в школьном курсе математического анализа. Дидактическое обеспечение дисциплины «Математика» позволяет составить систему учебных заданий, отвечающих сформулированным требованиям. После составления ДУ приводится иллюстрация техники выполнения необходимых преобразований для получения общего и частного решений.
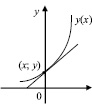
Такой подход создает благоприятные условия для активизации мыслительной деятельности, так как студенты первых курсов еще хорошо помнят многие математические понятия и формулы, которые им известны со школьного этапа обучения. Понятие касательной к графику функции в заданной точке, как правило, сохраняется в их памяти. В школьном курсе математического анализа они решали достаточное количество задач на эту тему. Они умеют находить угловой коэффициент касательной, вычисляя значение производной функции в заданной точке x0 (k = y´(x0)), и составлять ее уравнение (y – y(x0) = y´(x0)(x – x0)). В разделе производной функции в вузовском курсе математики студенты вновь встречаются с понятием касательной к графику функции в заданной точке. Их знания и умения расширяются и закрепляются при выполнении учебных упражнений на определение расположения касательной относительной различных прямых на координатной плоскости.
Если заданная точка имеет фиксированные значения координат, то угловой коэффициент касательной и ее уравнение представляют собой алгебраические выражения. Если координаты точки, через которую проходит касательная к графику функции, становятся текущими (изменяемыми), то угловой коэффициент касательной и ее уравнение рассматриваются как ДУ первого порядка (k = y´(x) и yi – y (x) = y´(x)(xi – x)).
Включение в процесс формирования понятия ДУ анализ решения задач на нахождение функции, если известно расположение касательной, позволяет создать наглядный образ взаимосвязи математических понятий, что всегда положительно сказывается на активизации мыслительной деятельности. Рисунок, отражающий условие учебной задачи с геометрическим содержанием, помогает визуализировать преобразование алгебраических уравнений в ДУ. Построение интегральных линий, изображающих искомую функциональную зависимость, после ее установления при нахождении частного решения ДУ, иллюстрирует соблюдение требований условия задачи и адекватность полученной математической модели.
Реализация предложенной выше методической идеи начинается с составления системы учебных задач на нахождение интегральной кривой, если задана функциональная зависимость углового коэффициента касательной или известно характерное расположение касательной на координатной плоскости [1, 3]. Можно выбрать, например, по три задачи на применение ДУ видов k = y´(x) и yi – y (x) = y´(x)(xi – x) . Изложение учебного материала о трех основных типах ДУ первого порядка (уравнение с разделяющимися переменными, однородное и линейное неоднородное) распределяется на три вида учебных занятий: лекционное, практическое и лабораторное.
Представляется целесообразным на лекции решить со студентами, подробно обсуждая в ходе эвристической беседы, три задачи с геометрическим содержанием на применение каждого рассматриваемого типа ДУ. Задачи, в которых требуется найти общее решение ДУ, желательно дополнить начальными условиями для нахождения частного решения. Это позволит выделить их особенности. Теоретический материал, необходимый для решения выбранных задач, структурируется по типам ДУ (таблица).
Формирование понятия о выделенных типах ДУ продолжается на практических занятиях. Студентам предлагается решить три задачи на применение уравнения касательной к графику функции в заданной точке. Задача Е: найти уравнение кривой, у которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат. Задача Q: найти уравнение кривой, если известно, что треугольник, образованный осью ординат, касательной к кривой в произвольной ее точке и радиус-вектором точки касания, равнобедренный, а основанием его является отрезок касательной от точки касания до оси ординат. Задача W: найти уравнение кривой, у которой площадь трапеции, образованная осями координат, ординатой произвольной точки и касательной в этой точке, равна половине квадрата абсциссы.
Классификация математических моделей задач по основным типам ДУ первого порядка
|
Угловой коэффициент касательной k = y´(x) |
||
|
|
Задача А. Найти уравнение линий, если известно, что угловой коэффициент касательной в любой точке каждой линии равен ординате этой точки, увеличенной в три раза. Задача В. Найти уравнение линий, если известно, что произведение углового коэффициента касательной в точке касания и суммы координат точки касания равно удвоенной ординате точки касания. Задача С. Найти уравнение линий, зная, что угловой коэффициент касательной в любой точке каждой линии равен сумме координат точки касания |
|
|
Математические модели задач (ММЗ) – ДУ первого порядка y´(x) = f(x, y) |
||
|
ММЗ А: k = 3y - y´(x) = 3y |
ММЗ В: k(x + y) = 2y - - y´(x)(x + y) = 2y |
ММЗ С: k = x + y - - y´(x) = x + y |
|
ДУ с разделяющимися переменными y´(x) = f(x)g(y) |
Однородное ДУ y´(x) = ´(y(x)/x) |
Линейное неоднородное ДУ y´(x) + p(x)y(x) = q(x) |
|
Способы решения |
||
|
1. Производная y´(x) выражается через отношение дифференциалов dy/dx. 2. Дифференциал dy и переменная y группируются в левой части уравнения, а дифференциал dx и переменная x – в правой части. 3. Интегрируется правая и левая части уравнения по переменным y и x соответственно |
1. Вводится новая функция t(x) = y(x)/x. 2. Функции y(x) и y´(x) заменяются соответственно на xt(x) и t(x)+xt´(x). 3. Уравнение y´(x)(x + y) = 2y принимает следующий вид (t(x)+xt´(x))(x+xt(x)) = 2xt(x). 4. Алгебраические преобразования приводят полученное уравнение к ДУ с разделяющимися переменными |
1. Решается линейное однородное ДУ z´(x) + p(x)z(x) = 0 с новой функцией z(x). 2. Функция y(x) записывается в виде y(x) = v(x)z1(x), где z1(x) – частное решение ДУ. 3. Функции y(x) и y´(x) подставляются в линейное неоднородное ДУ. 4. Уравнение приводится к ДУ с разделяющимися переменными |
|
Общее решение ДУ (y = y(x; C) или Ф(x; y C) = 0) |
||
|
y (x) = Ce3x |
y (x) = C(x – y(x))2 |
y(x) = – x – 1 + Cex |
|
Задача А1. Найти уравнение линии, проходящей через точку K(0; 2), если известно, что угловой коэффициент касательной в любой точке линии равен ординате этой точки, увеличенной в три раза |
Задача В1. Найти уравнение линии, проходящей через точку L(1; –1), если известно, что произведение углового коэффициента касательной в точке касания и суммы координат точки касания равно удвоенной ординате точки касания |
Задача С1. Найти уравнение линии, проходящей через точку N(0; –2), зная, что угловой коэффициент касательной в любой точке этой линии равен сумме координат точки касания |
|
Частные решения ДУ (y = y(x; C0) или Ф(x; y C0) = 0) |
||
|
y (x) = 2e3x |
y (x) = – 0,25(x – y(x))2 |
y(x) = – x – 1 – ex |
Студенты знакомятся с содержанием задач и изображают на рисунках условие каждой из них. Визуализация геометрических объектов позволяет правильно составить математические модели и определить тип ДУ. Обсуждается процесс нахождения общего решения трех типов ДУ. В дальнейшем в содержание каждой задачи вводится дополнительная информация о координатах некоторой точки, через которую должна пройти интегральная кривая. Формулируется содержание задач E1, Q1 и W1 аналогично задачам А1, В1 и С1 (таблица). Задаются координаты точек T(4;1), P(1; 0) и S(2; 1) соответственно для задач E1, Q1 и W1. Поиск частных решений не вызывает затруднений. В результате учебной деятельности у студентов формируется определенная система математических знаний о типах ДУ первого порядка.
Развитие понятия о частном решении ДУ может осуществляться на лабораторном занятии. Студентам предлагается выполнить состоящее из двух частей задание на построение интегральных кривых, используя систему компьютерной математики MathCAD [6]. В первой части задания им необходимо построить графики частных решений ДУ для задач А1, В1, С1, E1, Q1 и W1. Анализ полученных изображений функциональных зависимостей позволяет проверить соблюдение условий в каждой задачи и определить адекватность математических моделей. Во второй части задания требуется самостоятельно в каждой задаче задать координаты другой точки, через которую должна пройти интегральная кривая, найти такое частное решение, построить его график и оценить его достоверность.
Заключение
Соединение в единое целое лекционного, практического и лабораторного занятий по изучению ДУ с применением учебных задач с геометрическим содержанием, непроизвольно включает студентов в учебно-исследовательскую деятельность. Выполнение составленной системы дидактических заданий не только формирует знания и умения, но и развивает компетенции математического моделирования [5]. Проведение таких мыслительных операций как анализ и обобщение при решении ДУ создает благоприятные условия для развития культуры мышления [2] студентов в процессе обучения математике.