Эконометрика – наука об измерении и анализе экономических явлений с помощью математических и статистических методов и моделей. Простейшей эконометрической моделью является модель парной линейной регрессии, которая имеет вид:
, 
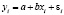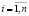. (1)
Неизвестные оценки параметров a и b модели (1) зачастую находятся по методу наименьших квадратов. При этом зависимая переменная y считается стохастической (случайной), а независимая переменная x – детерминированной (определенной). Однако переменная x в реальной ситуации также может иметь стохастический характер. В настоящее время хорошо изучены вопросы оценивания регрессионных моделей со стохастическими переменными, но плохо проработаны вопросы прогнозирования по ним.
Пусть оцененная полным методом наименьших квадратов [1,2] регрессия имеет вид:
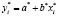, (2)
где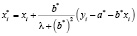 
, 
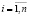– расчетные значения независимой переменной x, ? – заданное соотношение дисперсий ошибок по переменным y и x.
По уравнению (2) требуется получить прогнозное значение переменной y, если прогнозное значение переменной x равно x0. Для этого можно использовать методику, подробно рассмотренную в работе [3].
Если исследователь владеет информацией о том, как зависит переменная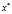 
от переменной x, то для получения прогноза необходимо определить расчетное значение независимой переменной 
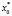при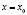 
и подставить его в уравнение (2). Таким образом, будет получен точечный прогноз 
.
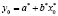Если исследователь не владеет информацией о том, как зависит переменная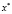 
от переменной x, то возможно получение интервального прогноза согласно следующей процедуре.
Для независимой переменной x определяется минимальное и максимальное значение ошибки аппроксимации:
, 
.
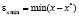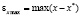Определяется интервал расчетных значений независимой переменной x: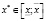 
, где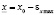 
, 
.
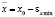Находится нижняя граница интервального прогноза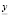 
. Для этого в уравнение (2) необходимо вместо переменной 
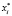подставить найденное на предыдущем шаге значение 
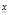или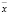 
по такому правилу: если коэффициент уравнения 
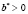, то вместо значения 
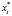подставляется 
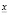, а если 
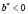, то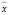 
.
По аналогии с предыдущим шагом, находится верхняя граница интервального прогноза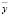 
. При этом подстановка осуществляется по такому правилу: если коэффициент уравнения 
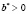, то вместо значения 
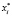подставляется 
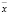, а если 
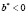, то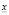 
.
Отметим, что по предыдущим двум шагам найден интервал для расчетных значений переменной y: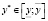 
. Для нахождения интервала для фактических значений переменной y необходимо использовать равенство
.
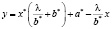