В данной статье мы рассмотрим уравнение вида
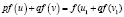 ,
,
где 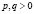 , p+q=1, u,v,
, p+q=1, u,v, 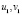 – функции относительно искомого неизвестного x; f – некоторая функция.
– функции относительно искомого неизвестного x; f – некоторая функция.
Для решения таких уравнений надо будет использовать понятия функции выпуклой на промежутке l и функции вогнутой на промежутке l.
Выпуклая функция – функция, графиком которой является выпуклая кривая. Выпуклая функция может быть выпуклой вверх (рис. 1) или выпуклой вниз (рис. 2). Иногда выпуклой называют только функцию, выпуклую вверх, а функцию, выпуклую вниз – вогнутой функцией.
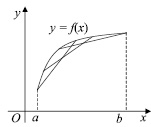
Рис. 1
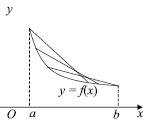
Рис. 2
Функция 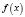 называется выпуклой вверх (вниз) на отрезке
называется выпуклой вверх (вниз) на отрезке 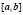 , если кажется дуга графика этой функции лежит не ниже (не выше) стягивающей ее хорды.
, если кажется дуга графика этой функции лежит не ниже (не выше) стягивающей ее хорды.
Более обстоятельно это определение выглядит так [3].
Определение 1. Пусть 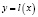 – уравнение прямой, проходящей через точки
– уравнение прямой, проходящей через точки 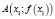 и
и 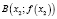 . Если
. Если 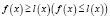 при
при 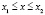 , где
, где 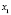 и
и 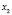 – любые точки на отрезке
– любые точки на отрезке 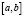 , то
, то 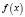 выпукла вверх (вниз). При этом если
выпукла вверх (вниз). При этом если 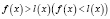 при
при 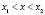 , то
, то 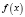 называется строго выпуклой вверх (вниз).
называется строго выпуклой вверх (вниз).
Из математического анализа известно, что функция непрерывная на отрезке 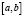 и дважды дифференцируемая на интервале
и дважды дифференцируемая на интервале 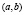 , является выпуклой вверх (вниз), тогда и только тогда, когда
, является выпуклой вверх (вниз), тогда и только тогда, когда 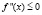
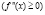 на этом интервале.
на этом интервале.
Функцию на выпуклость и вогнутость исследуют с помощью второй производной, но в ряде случаев это можно сделать элементарными методами.
Условие выпуклости и вогнутости графика функции заключается в следующем. Пусть функция у = f(x) определена на отрезке [a; b] и график функции на этом отрезке выпуклый (рис. 3). Возьмем на отрезке [a; b] два любых значения аргумента х1 и х2 (х1 < х2). Тогда значениями ординат точек А и В графика функции соответственно будут f(x1) и f(x2). Посредине между точками х1 и х2 возьмем точку
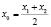 .
.
Тогда
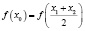 .
.
Так как по условию график функции выпуклый, то для любых значений х1 и х2 из отрезка [a; b] точка графика функции С должна лежать выше точки С1 хорды АВ, то есть DC > DC1. Из трапеции Ах1х2В находим ее среднюю линию
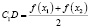 .
.
Таким образом, если график функции у = f(x) выпуклый на отрезке [a; b], то для любых двух значений аргумента х1 и х2 из этого отрезка должно выполняться неравенство
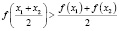 . (1)
. (1)
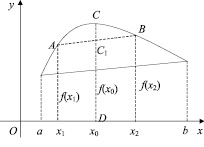
Рис. 3
Аналогично можно показать, что если график функции у = f(x) вогнутый на отрезке [a; b], то для любых значений х1 и х2 из этого отрезка выполняется неравенство
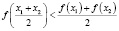 . (2)
. (2)
Справедливо и обратное утверждение: если для функции у = f(x), определенной на отрезке [a; b], при всех значениях х1, х2 из этого отрезка выполняется неравенство (1), то график функции на этом отрезке выпуклый, а если выполняется неравенство (2), то график функции на этом отрезке вогнутый.
Неравенства (1) и (2) есть необходимое и достаточное условия выпуклости и вогнутости графика функции.
Дадим несколько другой подход к понятию выпуклой функции [1, 2].
Определение 2. Функция f называется выпуклой на промежутке l (l – произвольный промежуток на Ox) если для любого отрезка 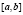 , принадлежащего l, и любого числа ?, ?
, принадлежащего l, и любого числа ?, ? 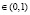 , выполняется неравенство
, выполняется неравенство
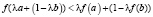 . (*)
. (*)
Определение 3. Функция f называется вогнутой на промежутке l, если для любого отрезка 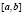 , принадлежащего l, и любого числа ?, ?
, принадлежащего l, и любого числа ?, ?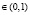 , выполняется неравенство
, выполняется неравенство
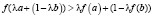 . (**)
. (**)
Неравенства (*) и (**) называются неравенствами Иенсена. Известен критерий выпуклости функции на промежутке [1]:
Теорема 1. Функция 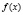 является выпуклой на промежутке l тогда и только тогда, когда для любых
является выпуклой на промежутке l тогда и только тогда, когда для любых 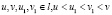 и любых
и любых 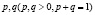 , таких, что
, таких, что 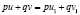 , выполняется неравество
, выполняется неравество
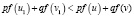 . (***)
. (***)
Теорема 2. Если функции f и q являются выпуклыми на промежутке l числовой прямой, то на этом промежутке их сумма 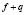 также выпукла.
также выпукла.
Теорема 3. Если в уравнении
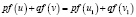
функция 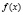 является строго выпуклой вверх или строго вогнутой вниз на промежутке X, функции
является строго выпуклой вверх или строго вогнутой вниз на промежутке X, функции
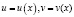 ,
, 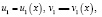
такие, что при всех x из области определения уравнения (D) их значения содержатся в X и выполняется условие 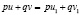 , то заданное уравнение на множестве
, то заданное уравнение на множестве
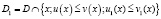
равносильно уравнению
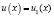 .
.
Задача. Найдите неположительные корни уравнения
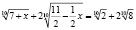 .
.
Решение
Областью определения заданного уравнения является решение системы
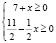 ,
,
то есть промежуток [–7;11].
Разделив обе части заданного уравнения на 3 (сумму коэффициентов при радикалах левой или правой частей уравнения), перепишем его в виде
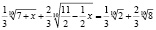 .
.
Это уравнение имеет вид
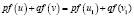 ,
,
где 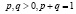 ,
,
при этом
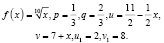
Функция 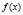 является строго выпуклой вверх на неположительной части числовой прямой. Действительно это так, потому что выполняется условие, отмеченное в теореме 1:
является строго выпуклой вверх на неположительной части числовой прямой. Действительно это так, потому что выполняется условие, отмеченное в теореме 1:
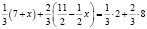 (3)
(3)
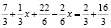
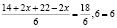 .
.
Множество D1, фигурирующее в теореме 3, для уравнения (3) есть множество [–7;0].
Таким образом, на отрезке [–7;0] исходное уравнение равносильно уравнению
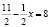 , откуда
, откуда 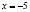 .
.
Следовательно, найденный корень единственный искомый отрицательный корень исходного уравнения.
Проверка показывает, что 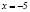 действительно является корнем исходного уравнения.
действительно является корнем исходного уравнения.
При 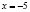 имеем:
имеем:
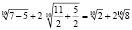 ,
,
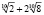 =
=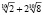 .
.
Для самостоятельного решения предлагаем задачи, заимствованные из работы [1].
Задача. Решите уравнение
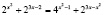 .
.
Ответ:
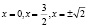 .
.
Задача. Найдите неотрицательные корни уравнения
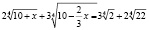 .
.
Ответ: 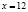 .
.
Задача. Найдите неположительные корни уравнения
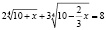 .
.
Ответ: 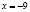 .
.
Задача. Решите уравнение
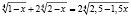 .
.
Ответ: 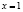
Задача. Решите уравнение
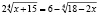 .
.
Ответ: 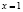 .
.
Задача. Решите уравнение
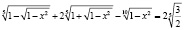 .
.
Ответ:
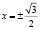 .
.

