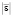Цель данной работы – установление количественных корреляций «структура –теплоёмкость» в алкенах с помощью феноменологических методов, основывающихся на концепции попарных и более сложных взаимодействий атомов в молекуле.
Для этого в работе проведена оценка состояния численных данных по теплоёмкости алкенов, выведены расчётные схемы. Так для алкенов в четвёртом приближении получаем:
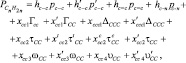
где С’ – атом углерода у двойной связи; Гcc и Г’cc – эффективные взаимодействия пар атомов С через один атом соответственно во фрагментах С–С–С и С=С–С, Dccc и D’ccc – соответствующие эффективные взаимодействия троек атомов С через один атом и т.д.
По данному уравнению был выполнен расчет теплоёмкости ряда алкенов.
Так как в результате нехватки экспериментальных данных получилась система с линейнозависимыми столбцами, то параметр ?cc пропадает, а параметры pc-c, pc-c’, pc=с, pc-н были заменены на параметр
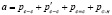 .
.
В табл. 1. представлены, найденные МНК значения параметров и результаты расчёта теплоёмкости ряда алкенов
Таблица 1
Параметры и результаты расчета теплоёмкости алкенов (в кДж/моль) в четвёртом приближении
|
Параметр |
а |
Гcc |
Г’cc |
Δccс |
Δ’ccс |
τcc |
τtcc |
τccc |
τ’cc |
ωcc |
ω’cc |
υ’cc |
|
Значения параметров |
8,782 |
20,081 |
-7,611 |
-33,885 |
-10,893 |
-3,291 |
4,022 |
-1,895 |
4,659 |
-1,169 |
-23,950 |
-9,560 |
|
|
1,2 |
|||||||||||
|
εmax |
5,7 |
Таблица 2
Результаты расчета теплоёмкости ряда алкенов (Дж/мольК)
|
№ |
Молекула |
С0р (г, 298 К) |
№ |
Молекула |
С0р (г, 298 К) |
||
|
Опыт [1] |
Расчет |
Опыт [1] |
Расчет |
||||
|
1 |
СН2=СН2 |
42,9 |
43,9 |
16 |
с-СН3СН2СН=СНСН2СН3 |
– |
165,6 |
|
2 |
СН2=СНСН3 |
64,3 |
62,6 |
17 |
t-СН3СН2СН=СНСН2СН3 |
– |
171,5 |
|
3 |
СН2=СНСН2СН3 |
85,7 |
86,0 |
18 |
СН2=С(СН3)(СН2)2СН3 |
135,6 |
136,6 |
|
4 |
с-СН3СН=СНСН3 |
78,9 |
79,5 |
19 |
СН2=СНСН(СН3)СН2СН3 |
142,4 |
137,8 |
|
5 |
t-СН3СН=СНСН3 |
87,8 |
85,4 |
20 |
СН2=СНСН2СН(СН3)2 |
126,5 |
126,5 |
|
6 |
СН2=С(СН3)2 |
89,1 |
90,6 |
21 |
(СН3)2С=СНСН2СН3 |
– |
151,5 |
|
7 |
СН2=СН(СН2)2СН3 |
109,6 |
113,2 |
22 |
с-СН3СН=С(СН3)СН2СН3 |
– |
150,7 |
|
8 |
с-СН3СН=СНСН2СН3 |
101,8 |
101,7 |
23 |
t- СН3СН=С(СН3)СН2СН3 |
126,6 |
132,3 |
|
9 |
t-СН3СН=СНСН2СН3 |
108,5 |
107,6 |
24 |
с-СН3СН=СНСН(СН3)2 |
133,6 |
133,1 |
|
10 |
СН2=С(СН3)СН2СН3 |
110,0 |
110,7 |
25 |
t-СН3СН=СНСН(СН3)2 |
141,4 |
139,0 |
|
11 |
СН2=СНСН(СН3)2 |
118,6 |
118,6 |
26 |
СН2=С(СН2СН3)2 |
– |
156,1 |
|
12 |
(СН3)2С=СНСН3 |
105,0 |
102,7 |
27 |
СН2=С(СН3)СН(СН3)2 |
– |
172,4 |
|
13 |
СН2=СН(СН2)3СН3 |
– |
165,3 |
28 |
СН2=СН(СН3)3 |
126,5 |
126,5 |
|
14 |
с-СН3СН=СН(СН2)2СН3 |
– |
139,0 |
29 |
(СН3)2С=С(СН3)2 |
123,6 |
124,1 |
|
15 |
t-СН3СН=СН(СН2)2СН3 |
– |
145,6 |
||||
Рассчитанные величины согласуются с экспериментальными и позволяют предсказать (в пределах ошибок опыта) недостающие значения свойств членов исследуемого ряда.
В табл. 2. представлены результаты расчёта теплоёмкости алкенов с С2–С6.