Доминантным условием обеспечения стабильного экономического развития любого государства является создание эффективной системы межбюджетных взаимоотношений регионов с федеральными органами власти и местным самоуправлением. В этих отношениях ключевой составляющей является межбюджетное регулирование, представляющее собой набор действий по распределению финансовых ресурсов между бюджетами различных уровней иерархии бюджетной системы. В статье излагаются результаты создания модели игрового поведения стохастических автоматов с целью поддержки принятия решений при долевом распределении налоговых поступлений между бюджетами, обеспечивающих компромисс интересов бюджетов вышестоящего и нижестоящего уровней бюджетной системы РФ. Взаимодействующие между собой автоматы, обозначенные переменными A1 и A2, управляют назначением величин отчислений от уплаты налогов соответственно в бюджеты нижестоящего и вышестоящего уровней бюджетной системы посредством выбора своих состояний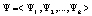 
. Структура автоматов и стратегия их поведения в стационарных [1,2,3,4] и нестационарных [5] случайных средах описана ранее. Для формализации этого взаимодействия в статье предложена теоретико-игровая модель 
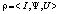, где 
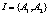– множество игроков, в роли которых выступают системы A1 и A2; 
, 
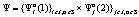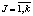– декартово произведение стратегий, доступных игрокам A1 и A2; 
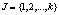– множество номеров состояний автоматов; 
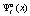– стратегия, доступная игроку x, 
; ?, 
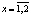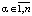– случайная среда, в которой функционирует автомат; k – количество состояний автомата; n – количество случайных сред системы «автомат-переключаемая среда»; 
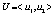– набор функций выигрышей игроков A1 и A2 соответственно, представляющих собой 
, 
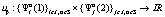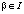и ставящих в соответствие каждому набору стратегий 
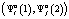выигрыш этого игрока 
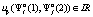. Вследствие того, что множество игроков 
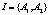и стратегий 
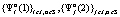конечны (мощности этих множеств составляют соответственно 
, 
, 
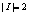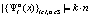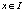), игра 
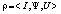формально описывается в виде матрицы 
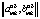, элементами которой являются числа 
, 
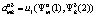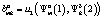, представляющие собой соответственно выигрыши игроков A1 и A2 в стратегиях 
, 
, 
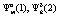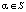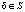. В качестве выигрыша игрока A1 при наборе стратегий 
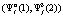примем вероятность выигрыша системы «автомат-переключаемая среда», величина которой определяется в соответствии с аналитическими выражениями: 
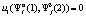если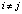 
; 
; 
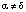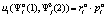, если i=j; 
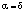, где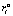 
– финальная вероятность выбора системой «автомат-переключаемая среда» состояния 
; 
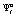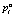– оценка вероятности выигрыша системой автомат-переключаемая среда» в состоянии 
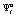. Выигрыш игрока A1, имеющий вид 
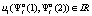, обозначим переменной 
: 
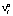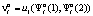. Относительно выигрыша игрока A2, как упоминалось, полная информация отсутствует. Обозначим этот выигрыш следующим образом: 
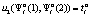. Вследствие того, что игрокам A1 и A2 доступны одинаковые стратегии, в выражениях 
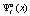, обозначающих их стратегии, далее значение переменной 
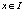будут опущены. На множестве чистых стратегий 
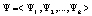, доступных игрокам A1 и A2, зададим вероятностное распределение 
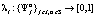, ставящее в соответствие каждой чистой стратегии 
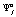игрока i, 
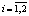вероятность 
, 
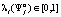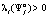того, что эта стратегия будет играться игроком 
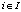, причём выполняется условие
.
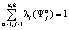Тогда будем иметь пространство наборов смешанных стратегий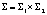 
, где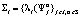 
, 
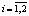– набор смешанных стратегий игрока Ai . Носителем смешанной стратегии ?i является множество чистых стратегий 
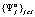, которым приписана положительная вероятность. Будем рассматривать смешанное расширение 
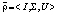игры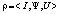 
, где ? – множество чистых стратегий, которые игрок A1 играет с положительными вероятностями в ситуации 
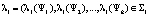, а игрок A2 играет с положительными вероятностями в ситуации 
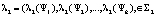. Смешанные стратегии игроков A1 и A2 будем искать исходя из условия равновесия по Нэшу в смешанном расширении 
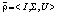, в соответствии с которым при заданном распределении вероятностей противника ожидаемый выигрыш от применения чистых стратегий одинаков при любой стратегии противника. Только в данном случае при нахождении смешанных стратегий необходимо учесть тот факт, что игрок A1 знает свою функцию выигрыша 
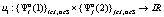, но не знает функции выигрыша игрока A2. То есть возникает задача описания ситуации с неполной информацией, когда игрок A1 сталкивается с некоторой неопределённостью относительно выбора стратегии игроком A2. В этой ситуации выдвинем следующую гипотезу. Примем, что величина выигрыша 
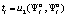игрока A2 при выборе стратегии 
, 
, 
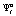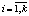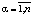распределена равномерно на отрезке 
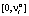. Правомерность этого предположения можно обосновать тем, что ЛПР в финансовых управлениях бюджетом вышестоящего уровня бюджетной системы РФ ввиду его заинтересованности в экономическом развитии всей территории и в зависимости от характера решаемых в данный период задач может с равной вероятностью считать и своим выигрышем тот выигрыш, который получен при управлении бюджетной системой нижестоящего уровня.
Игрок A2 будет играть свою стратегию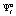 
, если его выигрыш 
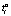от неё будет больше или равен некоторого заданного числа 
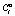, т.е. если 
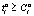. Вероятность этого условия может быть определена следующим образом: 
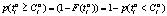. Очевидно, что вероятность выполнения условия 
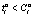определяется из выражения 
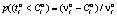. Тогда вероятность выполнения условия 
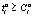составит 
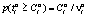. Эта вероятность рассматривается как вероятность выбора игроком A2 стратегии 
: 
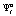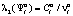. Игрок A1 предпочтёт свою стратегию 
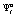, если его выигрыш 
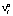в этом случае будет максимально возможным. А это может быть выполнено лишь в том случае, когда большая часть налоговых доходов при бюджетном регулировании поступит в бюджет нижестоящего уровня. Но в этом случае выигрыш игрока A2 будет меньше некоторой величины 
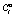. Напомним, что вероятность выполнения этого условия определяется как 
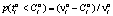и совпадает с вероятностью выбора игроком A1 стратегии 
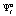. Эта вероятность рассматривается как вероятность 
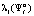выбора игроком A1 своей стратегии 
: 
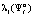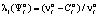. Используя условие равновесия по Нэшу, имеем выражение для
.
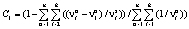С учётом принятого ранее обозначения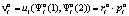 
, величина C1 будет определяться следующим образом:
,
,
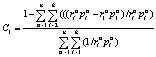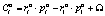где
.
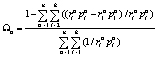Тогда выражения для вероятностей выбора игроком A1 стратегии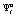 
имеет вид
.
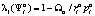Смешанные стратегии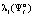 
используются как коэффициенты для определения нормативов отчислений S в бюджет нижестоящего уровня бюджетной системы РФ по налогу вида : 
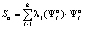. Полученные выражения положены в основу алгоритмов определения величин процентных отчислений от уплаты налогов в порядке бюджетного регулирования.