Вероятностные представления возникли достаточно давно и оформились в 15–16 вв. усилиями П. Ферма, Б. Паскаля, Я. Бернулли, Х. Гюйгенса и др. По мере накопления вероятностных знаний стали возникать сложности чисто вычислительного характера: подсчет факториалов даже небольших чисел, нахождение степеней действительных чисел, исчисление мер и т.п. Вычислительная математика того времени, как могла, помогала преодолевать возникающие сложности, однако ее возможности были весьма ограничены, что несколько тормозило развитие теории вероятностей. В 19 веке вовсю стала развиваться статистика, выделилась математическая статистика. Необходимость обработки больших массивов данных стала одной из важнейших математических проблем. В первой половине 20 века была создана усилиями К. Пирсона, Р. Фишера, У. Госсета (Стьюдента) и др. современная математическая статистика, разработаны основные методы и процедуры. И опять возникает проблема вычислений, которые можно охарактеризовать как рутинные. Разрабатывались специальные приемы «ручных» вычислений типа метода четырех полей для обработки корреляционной таблицы. Со временем возникали новые статистические дисциплины (например, эконометрика) с растущим стремительно объемом рутинных вычислений.
В итоге ситуация стала таковой, что изучение вероятностно-статистических закономерностей невозможно представить без проведения рутинных расчетов. Естественно, устный и ручной счет совершенно не удовлетворял потребностям практики. Стали необходимы вычислительные приспособления. В первой половине 20 века инструментом, помогающим выполнять арифметические операции при нахождении значений статистических величин, служила обычная логарифмическая линейка. Кроме того, большую роль стали играть статистические таблицы. Кроме чисто практического значения, работа с таблицами имела и дидактические функции: содержание, структура и последовательность вычислений раскрывалась с помощью таблиц. В результате правильно организованной работы с таблицами в сознании студента, изучающего теорию вероятностей и математическую статистику, формировалась карта взаимосвязей понятийного аппарата. Преподаватель имел возможность, опираясь на систематизированный табличный материал, организовать обсуждение особенностей вероятностных и статистических понятий.
Развитие микропроцессорной техники привело к широкому использованию во второй половине 20 века в образовательном процессе различных калькуляторов, которые вытеснили явно устаревшую к тому времени логарифмическую линейку. Некоторые алгоритмы расчетов хранились в памяти вычислительной техники, поэтому часть вычислений полностью автоматизировалась. Карта процесса нахождения значений вероятностных и статистических величин изменилась. Многие взаимосвязи понятий уже не формировались должным образом в сознании студентов, что приводило к недостаточному, на наш взгляд, осознанию характера вероятностно-статистических закономерностей.
Стремительное вторжение во все сферы образовательного пространства современных информационно-компьютерных технологий (ИКТ) в 21 веке предоставило возможность полной автоматизации всех вычислительных процессов, связанных со статистическими расчетами. Однако, и это крайне важно для образовательного процесса, программы статистических вычислений скрывают от пользователя алгоритмы вычислений. В сознании студентов при использовании ИКТ не формируется та карта взаимосвязей вероятностно-статистических понятий, без которой невозможно ни понимание, ни усвоение теории вероятностей и математической статистики, что в результате приводит к непониманию получаемых результатов вычислений. Искаженное восприятие существенных закономерностей объективной реальности не позволяет студентам корректно интерпретировать наблюдаемые явления и процессы в природе, технике и социуме.
Цель исследования
Овладение студентами экономических направлений подготовки вероятностно-статистическими методами представляется крайне важным. Успешное развитие экономики в постиндустриальном обществе невозможно прогнозировать без использования вычислительной техники для принятия научно-обоснованных решений, учитывающих воздействие огромного количества случайных факторов. Стремление дальнейшего совершенствования процесса преподавания теории вероятностей и математической статистики в вузе ставит целью данного исследования проектирование требований к дидактическим заданиям, обеспечивающих оптимизацию синтеза педагогических технологий (ПТ) и ИКТ при организации учебной деятельности студентов.
Материалы и методы исследования
Описания психолого-педагогических и научно-методических закономерностей по вопросам развития мыслительной деятельности и формирования понятий теории вероятностей и математической статистики выступают материалами представленного исследования. Достижение поставленной цели осуществляется при использовании в исследовательской деятельности таких методов, как педагогическое наблюдение дидактических явлений и процессов, поэлементный анализ научных публикаций, пооперационный анализ учебной деятельности, моделирование взаимосвязей компонентов ПТ и ИКТ.
Результаты исследования и их обсуждение
Включение ИКТ в процесс преподавания математики в вузе анализируется в работах [4, 5]. Авторы [5] на основе полученных результатов обосновывают целесообразность использования ИКТ, но не определяют траекторию движения мыслительной деятельности студентов при решении задач с помощью ИКТ. Подробное изложение процесса решения учебных задач по математике в публикации [4] не затрагивает вопросы формирования математических понятий, а концентрирует внимание на чисто технической стороне применения ИКТ студентами вуза при выполнении типовых дидактических заданий.
Интересный подход к изложению теории вероятностей и математической статистике в вузе предложен В.В. Афанасьевым [1]. Сквозная методическая линия гармоничного сочетания вербального и графического структурирования учебного материала оригинально отображает существенные взаимосвязи вероятностно-статистических закономерностей. Представлен процесс решения разнообразных учебных задач, но без использования ИКТ. Применение в педагогической практике графического выражения мыслительного процесса в виде интеллектуальных карт [2] получает широкое распространение при изучении различных дисциплин и, безусловно, заслуживает внимания.
Вероятностно-статистические методы в вузовском курсе математики рассматриваются как совокупность действий по проверке гипотез о математических моделях распределений и взаимосвязей случайных величин. Применение математических моделей в процессе учебного познания включает прохождение трех этапов: 1) построение моделей; 2) изучение свойств и особенностей моделей; 3) интерпретация полученных результатов [3, с. 8–10]. Первый этап предполагает описание формальным математическим языком содержательных свойств объективной действительности. Второй этап предусматривает решение составленных уравнений или неравенств в виде математической задачи. Третий этап выявляет степень верификации математической модели при сравнении полученных значений искомых величин с известными фактами или экспериментальными данными. Прохождение представленных логически взаимосвязанных этапов особенно необходимо при изучении вероятностно-статистических методов, так как в этом случае у студентов целенаправленно формируются аналитико-синтетические умения. Наличие таких умений позволяет более эффективно отделять целое от его части, существующее реально от его образа в сознании, содержательную взаимосвязь от формальной конструкции.
Представляется продуктивным сформулировать следующие требования к дидактическим заданиям, предназначенным для формирования у студентов умений осмысленно решать задачи по теории вероятностей и математической статистике при активном использовании ИКТ: 1) стимулирование вербального и образного компонентов мышления студентов в дуалистическом единстве; 2) организация рассуждений о взаимосвязях элементов вероятностно-статистических моделей; 3) раскрытие содержания и структуры вычислительных процедур при нахождении значений вероятностно-статистических величин средствами ИКТ. Предложенные требования позволяют организовать в учебном процессе эффективное сочетание ПК и ИКТ при прохождении дидактического цикла по следующей схеме:
осведомленность > понимание > усвоение > актуализация и применение.
Применение средств педагогических технологий на каждом этапе цикла направлено, в первую очередь, на формирование существенных признаков и взаимосвязей понятия вероятностно-статистических методов. Включение ИКТ должно обеспечить автоматизацию вычислительных процедур нахождения значений тех величин, смысловое содержание которых освоено студентами на предшествующем этапе представленного выше цикла. Дидактические единицы (ДЕ) «независимые повторные испытания» и «доверительное оценивание» выступают основой формирования понятия «вероятностно-статистические методы» при изучении теории вероятностей и математической статистики, поэтому представляется целесообразным использовать их для иллюстрации изложенных выше методических идей (табл. 1 и 2).
Таблица 1
Модель взаимосвязи ПТ и ИКТ в дидактическом цикле для дидактической единицы «Независимые повторные испытания»
|
Этапы цикла |
Содержание ПТ |
Объект автоматизации ИКТ |
|
Осведомленность |
Вероятность Pn(k) наступления события А ровно k раз в n испытаниях определяется по точной формуле Бернулли или по приближенным формулам (формула Пуассона, локальная и интегральная теорема Муавра-Лапласа) |
Вычисление факториалов и сочетаний. При этом нахождение значений функций Лапласа и Пуассона целесообразнее определять по обычным статистическим таблицам |
|
Понимание |
Для обоснования вычисления Pn(k) по формуле Бернулли следует рассматривать совокупность всех возможных комбинаций наступления и ненаступления события А, а также использовать формулы комбинаторики |
Расчет не только сочетаний, но и вероятностей Pn(k) при различных значениях n, p и k |
|
Усвоение |
При достаточно большом количестве испытаний n и некоторых простых условиях интегральная теорема Муавра-Лапласа позволяет найти вероятность того, что частота k наступления события А отличается от np на некоторую положительную величину Δ |
Расчет вероятностей по формулам Бернулли, Лапласа, Пуассона и построение графических моделей плотности распределения вероятностей (наглядное отображение закономерностей статистических таблиц) |
|
Актуализация и применение |
Относительная частота k/n наступления события А заключается в некоторых пределах и отличается от вероятности р на некоторую величину ε с определенной вероятностью Р. Значение Р при больших n устанавливается функцией Лапласа, в зависимости от р и ε. При бесконечном возрастании n относительная частота k/n и вероятность р отличаются сколь угодно мало с вероятностью Р, сколь угодно близкой к 1 (закон больших чисел Бернулли) |
Процедура оценки отклонения на некоторую величину ε относительной частоты k/n наступления события А от вероятности р его наступления в одном испытании с заданной вероятностью Р |
Таблица 2
Модель взаимосвязи ПТ и ИКТ в дидактическом цикле для дидактической единицы «Доверительное оценивание»
|
Этапы цикла |
Содержание ПТ |
Объект автоматизации ИКТ |
|
Осведомленность |
Наряду с точечным оцениванием |
Вычисление выборочных характеристик |
|
Понимание |
Границы интервала |
Расчет точечных оценок выборочной средней и дисперсии. При этом, вычисление значений граничных статистик целесообразнее проводить с применением обычных статистических таблиц |
|
Усвоение |
Не θ попадает в доверительный интервал |
Нахождение значений граничных статистик при различных значениях надежности γ для выборочной средней и дисперсии (составление сравнительных таблиц отражает взаимосвязь надежности γ и точности δ) |
|
Актуализация и применение |
Величины γ и δ выбираются сообразно специфике задачи и целям исследования. Увеличение объема выборки n является, по сути, источником дополнительной информации о θ, что естественно позволяет повысить точность δ и увеличить надежность γ |
Процедура вычисления граничных (критических) значений применительно к проверке статистических гипотез |
Остановимся подробнее на объекте автоматизации.
Дидактическая единица «Независимые повторные испытания». Вычисление факториалов, числа сочетаний – проблема значительная. Однако полностью автоматизировать решение этой задачи не следует. Нахождение «небольших» факториалов и сочетаний, с дидактической точки зрения, лучше проводить «вручную». В этом случае понятнее становится формула Бернулли. Как только такие упражнения становятся рутинными и больше не несут дидактической нагрузки в контексте рассматриваемого выше дидактического цикла, вычисления следует автоматизировать. При рассмотрении приближенных формул Лапласа основная трудность традиционно состояла в иллюстрации нормального распределения как асимптотики биномиального распределения. Здесь автоматика играет решающую роль: меняя значения n и p, составляя различные сравнительные таблицы и графики, студенты могут реально почувствовать, как точки дискретного биномиального распределения постепенно вписываются в кривую непрерывного нормального распределения. Без автоматики достичь описываемого дидактического эффекта, характеризующего усвоение материала, просто невозможно. Еще одна важная дидактическая задача – обоснование выбора приближенной формулы (Лапласа или Пуассона). Традиционные рекомендации носят рецептурный характер, и принимаются «на веру». Разумеется, это не способствует пониманию, а тем более усвоению материала. Автоматизация вычислений легко позволяет достаточно убедительно провести различие между приближенными формулами: можно составить сопоставительную таблицу вычисления вероятностей по формулам Бернулли, Лапласа и Пуассона. Тогда становится понятным, почему в той или иной ситуации применяется та или иная приближенная формула. На этапе актуализации и применения использование автоматических вычислений можно проводить не пошагово, а целиком: по значениям параметров p, n и k сразу получать вероятности Pn(k) и суммы этих вероятностей.
Дидактическая единица «Доверительное оценивание». Вычислительные трудности здесь можно разделить на две группы. Первая связана с обработкой вариационного ряда и получением выборочных характеристик (среднее, дисперсия и др.), которые являются точечными оценками соответствующих генеральных числовых характеристик. Мы полагаем, что эти величины следует находить с помощью автоматических вычислений, поскольку эти самые вычисления достаточно знакомы студентам (ДЕ «Описательная статистика и выборочные характеристики вариационного ряда» предшествует ДЕ «Доверительное оценивание»). А вот вычисление граничных статистик 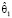 и
и 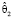 на первых порах эффективнее производить вручную (с помощью обычного калькулятора). Это важно для того, чтобы студенты обратили внимание, какие величины входят в выражения для граничных статистик. Далее, для понимания вопроса об изменении доверительного интервала в зависимости от величин γ, δ и n вполне уместно подключить автоматику: на этом этапе важны результирующие границы интервалов, а не детали их вычисления.
на первых порах эффективнее производить вручную (с помощью обычного калькулятора). Это важно для того, чтобы студенты обратили внимание, какие величины входят в выражения для граничных статистик. Далее, для понимания вопроса об изменении доверительного интервала в зависимости от величин γ, δ и n вполне уместно подключить автоматику: на этом этапе важны результирующие границы интервалов, а не детали их вычисления.
Заключение
Проведенное исследование позволяет сделать ряд важных педагогических выводов.
1. Информационно-компьютерные технологии являются важным фактором в процессе обучения студентов вероятностно-статистическим методам.
2. Применение ИКТ в курсе теории вероятностей и математической статистики должно быть дидактически выверено, подчиняться определенным дидактическим закономерностям. Предложенный авторами дидактический цикл позволяет корректно решать проблемы, возникающие в реальном учебном процессе.
3. Авторы полагают, что предложенный и обоснованный выше подход к оптимизации синтеза ПТ и ИКТ может быть применим к преподаванию других математических дисциплин, а также к преподаванию других дисциплин естественнонаучного цикла.


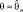 существует доверительное оценивание
существует доверительное оценивание 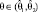
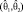 являются случайными величинами (статистиками). Утверждение
являются случайными величинами (статистиками). Утверждение 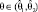 не абсолютно верно, а является случайным событием, т.е. имеет вероятность (надежность). Эта надежность γ близка к 1
не абсолютно верно, а является случайным событием, т.е. имеет вероятность (надежность). Эта надежность γ близка к 1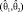 , а доверительный интервал
, а доверительный интервал 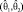 «накрывает» θ с заданной надежностью. Невозможно одновременно увеличить надежность оценки γ и повысить ее точность
«накрывает» θ с заданной надежностью. Невозможно одновременно увеличить надежность оценки γ и повысить ее точность 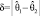 . Увеличивая γ, мы неминуемо снижаем точность δ и расширяем границы доверительного интервала
. Увеличивая γ, мы неминуемо снижаем точность δ и расширяем границы доверительного интервала