В системе задач школьного курса математики, безусловно, необходимы задачи, направленные на формирование математических знаний, умений и навыков, задачи иллюстративного характера, тренировочные упражнения, выполняемые по образцу. Но не менее необходимы задачи, направленные на развитие устойчивого интереса к изучению математики, творческого отношения к учебной деятельности. Необходимы специальные задачи для обучения школьников способам самостоятельной деятельности, общим приемам решения задач, для овладения ими методами научного познания реальной действительности, которыми пользуются ученые-математики, решая ту или иную задачу. К сожалению, в практике обучения математике задачи чаще всего рассматриваются лишь как средство сознательного усвоения учащимися программного материала.
Поэтому развитие исследовательских способностей старшеклассников очень актуально, т. к. в процессе обучения необходимо привить ученику стремление к самостоятельному пополнению своих знаний, содействовать к побуждениям, расширять свой кругозор, поддерживать интерес к предмету, к процессу познания. На основании анализа различных трактовок понятия «исследование» сделан вывод о том, что чаще всего его связывают с научным познанием. В школьном обучении «исследование» – это имитация творческого поиска исследователя.
Целью развития исследовательских способностей старшеклассников является развитие личности ученика, раскрытие его способностей, понимание логики математического мышления и использование этой логики в рамках других предметов. Как писал великий русский педагог К.Д. Ушинский: «Если сам ученик выработает мысль, самостоятельно освоив новое знание, то мысль эта сделается его собственностью». Исследовательские способности учащихся формируются и проявляются в учебной деятельности. В этом случае мы рассматриваем исследовательскую деятельность, как один из видов учебной деятельности, которая заключается в самостоятельном решении проблем познавательного и практического характера, задач повышенной трудности, нестандартных задач учащимися. На основе анализа положений работ Н.Я. Канторовича, М.В. Кларина, А.И. Савенкова, Т.Н. Шамовой и др. в качестве основного выбрано определение исследовательской деятельности как особого вида интеллектуально-творческой деятельности, порождаемой результатом функционирования механизмов поисковой активности и строящейся на базе исследовательского поведения. При исследовательской деятельности учащиеся отыскивают не только пути решения поставленных проблем, но и побуждаются к самостоятельной их постановке, к выдвижению целей своей деятельности. Учащиеся проходят те же этапы исследовательского процесса, что и настоящий исследователь, вследствие чего открывают для себя новое. Конечно же, это новое субъективно, новое для учащегося, а не для науки.
Школьный курс геометрии как нельзя лучше дает возможность развития исследовательской и творческой деятельности учащихся. Исследовательскую деятельность учащихся при обучении геометрии многие ученые (В.А. Далингер, Л.З. Карелин, Д. Пойа) связывают с решением исследовательских задач. Под исследовательскими задачами они понимают задачу, решение которой полностью или частично реализует учебное исследование, которое отличается от научного только субъективной новизной результата, либо учебное исследование может быть реализовано в ходе дополнительной работы над данной задачей. Такие задачи являются хорошей базой для развития основных исследовательских умений: анализа ситуации, условий; выдвижения гипотезы; выбора методов; составления плана решения; анализа результата; проверки решения для крайних, частных, новых случаев – установления следствия полученной закономерности.
В организации исследовательской деятельности учащихся имеют место определенные трудности. Во-первых, уровень математической подготовки не всегда позволяет организацию исследовательской деятельности учащихся, поэтому требуется осуществлять дифференцированный подход к обучаемым, во-вторых, для этой цели учителю необходимо подобрать или переконструировать задачи из учебника, для чего затрачивается дополнительное время. К системе исследовательских задач можно отнести задания на самостоятельное составление задач, аналогичных решенным; обратных решенным; составление задач на заданную тему; на определенный метод решения; задачи с неполным условием, практические задачи; решение задачи различными способами, рассмотрение частных и предельных случаев; поиск всех возможных решений задачи и т.д. При самостоятельном решении нестандартных задач также имеет место исследовательская деятельность.
В научно-методической литературе выделяют три этапа развития исследовательских способностей: репродуктивный, этап исследования в знакомой ситуации и этап включения в творческую деятельность.
На первом этапе учащимся даются задания на воспроизведение учебного исследования по имеющемуся образцу. Для этого достаточно двух-трех заданий, показанное учителем решение одного из них и будет служить тем образцом. Некоторым учащимся при необходимости можно предложить и дополнительные задания. На втором этапе учебное исследование проводится со знакомыми фигурами и отношениями между ними, основываясь на опытной проверке или на личном учебном опыте. На этапе включения в творческую деятельность проводится учебное исследование, в процессе которого открывается новое свойство знакомых или новых фигур или новый метод решения задачи. Также могут быть использованы задачи на усвоение материала, не входящего в общеобразовательную программу обучения, и задачи, требующие от учащихся применения нестандартных приемов решения. В таких случаях учащиеся не всегда могут справиться с решением до конца самостоятельно или это требует много учебного времени. Для достижения дидактической цели достаточно проведения опытной проверки – построения чертежа, на основе чего учащийся может предвидеть результат.
Рассмотрим решение следующей стереометрической задачи вместе с учащимися. Основной целью является изучение зависимости объема правильной треугольной пирамиды от величины плоского угла при вершине. Для нахождения идеи решения этой задачи учащимся нридется провести сложную мыслительную работу по анализу условия задачи. С помощью наводящих вопросов учитель может подвести учащихся к построению плана решения задачи, выдвижению гипотезы.
Задача. В правильной треугольной пирамиде SАВС плоский угол при вершине равен a, а кратчайшее расстояние между боковым ребром и противоположной стороной основания равно d. Найти объем этой пирамиды.
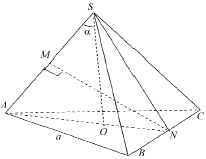
Решение. Проведем плоскость через ребро SА и точку N и основание перпендикуляра АN к отрезку ВС. Пусть NМ – высота треугольника АSN. Отрезок NМ, перпендикулярный к АS и ВС, равен d (рисунок). Обозначим через а сторону основания.
Тогда
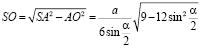 .
.
Так как АN ·SO=АS·d, то
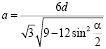 .
.
В результате имеем:
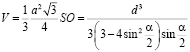 .
.
Для получения исследовательского эффекта учащимся предлагается самостоятельно «исследовать» случаи при a = 60°, 90°, 120° и сделать соответствующие выводы провести критический анализ результата решения. Также можно подобрать числовые данные к условию задачи или дополнить их новыми данными.
Рассмотрение таких исследовательских задач позволяет преодолеть рутинную повседневность уроков, сделать учебный процесс интереснее, расширить кругозор, стимулировать умственную активность учащихся, тем самым выявляя математические способности и развивая устойчивый интерес к математике. Полученные учащимися результаты приводят к «открытию» математических фактов, создают ощущение успеха, удовлетворенности, которые являются психологическим стимулом возникновения, поддержания и укрепления познавательных интересов. Следовательно, систематическое включение учащихся в исследовательскую деятельность является важным фактором формирования математического мышления и воспитания учащихся в процессе обучения.
Однако определение системы геометрических задач, направленных на формирование у учащихся умения самостоятельно и творчески изучать предмет, тем самым создавать предпосылки к активному применению математических знаний, в дальнейшем является одной из методических проблем, требующих внимания.

