Внедрение компетентностного подхода к обучению к 2020 г. входит в одну из задач системы образования Кыргызской Республики [1]. Основным непосредственным результатом образовательной деятельности с позиции компетентностного подхода становится формирование ключевых компетентностей [2]. Направленность компетентностного подхода к обучению: на «формирование умений учиться; ориентироваться в ситуации неопределенности и принимать решения на основе анализа информации; коммуникативных способностей; аналитических навыков и критического мышления» [3, с. 19] – отвечает содержанию подготовки школьников к математическим олимпиадам. И олимпиадная задача выступает при этом как инструмент определения уровня сформированности умений учиться, взаимодействовать в группе, работать с разными источниками информации [4]. А участие в математических олимпиадах формирует навыки научно-исследовательской деятельности учащихся, одновременно способствуя саморазвитию и самореализации их личности. Таким образом, очевидны возможности олимпиады в реализации компетентностного подхода в обучении олимпиадной математики. При обучении математике школьник знакомится со следующими типами задач:
– учебная – задача с известным алгоритмом решения, тренировочного характера;
– олимпиадная – задача с неизвестным способом решения, нестандартная;
– исследовательская – комплексная задача с неопределенным условием, проблемно-поисковая.
Учителю важно соотнести содержание задач олимпиады с содержанием школьного образования, поэтому к содержанию олимпиадных задач предъявляются особые требования.
Определяя понятие олимпиадных задач, одни авторы характеризуют их, как «не просто упражнения на проверку знаний и применение стандартных школьных приемов, а чаще всего теоремы, которые нужно доказать, задачи на отыскание... требующие некоторого исследования» [5, с. 3]. Другие, авторы задач Всероссийских олимпиад школьников акцентируют важность и необходимость включения в олимпиады заданий нового типа: «математические способности – это способности к построению новых для ученика логических конструкций, поэтому наиболее эффективно свою основную задачу открытия молодых талантов решают олимпиады, составленные из новых задач» [6, с. 14].
Анализируя тематику и содержание олимпиадных задач в [7], мы определили, что в задания разных уровней олимпиады включают задачи:
– составленные на основе программ по математике для общеобразовательных учебных учреждений, в качестве сложных допускаются задачи, тематика которых входит в программы кружков и школы олимпийского резерва;
– разного уровня сложности из разделов школьной математики, изученных к моменту проведения олимпиады: арифметика, алгебра, тригонометрия, комбинаторика, теория чисел, геометрия, математический анализ;
– задачи с нарастающим уровнем сложности;
– задания нового типа особенно важны.
Проецируя собственный опыт работы в жюри городских и областных олимпиад с 1994 г., считаем, что оценивание олимпиадных работ учащихся должно основываться на критериях оценки олимпиадной деятельности учащихся, а именно:
1) оценка собственных достижений – использование знаний внешкольной программы данного возраста;
2) эрудиция ученика в области олимпиадной математики – использование известных научных фактов;
3) защита результатов олимпиадной работы – четкая логика изложения, аргументированное обоснование решений, оригинальность рассуждений, умение защитить свою точку зрения при проведении апелляции.
Задания III этапа олимпиады школьников 2016–2017 учебного года в Кыргызстане состояли из трех задач, на решение которых было отведено 4 часа. Результаты олимпиады, требования к олимпиадным работам, оформление документации освещены в [8, с. 166–173]. Задача считалась полностью решённой с начислением максимально возможного количества баллов, только если в тексте решения были приведены все необходимые преобразования и полностью объяснены все имеющиеся логические шаги, при этом полученные ответы приведены к упрощённому виду. Если верный ответ не подкреплялся решением, со всеми обоснованными пояснениями, то задача считалась нерешенной.
Для уменьшения субъективизма при оценке решений были приняты градации:
1. Задание выполнено правильно и полностью, оформлено без замечаний и в надлежащем виде – 7 баллов.
2. Задание выполнено правильно, но упущены несущественные детали или оформлено с погрешностями – 6.
3. Задание выполнено правильно, но ответ не получен: осталось 1–2 шага до ответа – 5.
4. Задание выполнено правильно более, чем на половину – 4 б.
5. Выполнены предварительные шаги, к примеру при решении текстовой задачи правильно составлена система и сделана попытка решения системы или, при решении геометрической задачи, в чертеже выполнены дополнительные построения для решения задачи, сделано несколько шагов и т.д. – 3 б.
6. Записаны формулы, касающиеся задания, но решение задания не начато – 2 б.
7. На усмотрение проверяющего при оценивании задания предусматривается добавление 25 %, 50 %, 75 % от балла.
Предлагаем учителям методические рекомендации для проверки олимпиадных работ:
а) предварительно просмотрите свою задачу во всех работах. Определите различные способы решения этой задачи, типичные ошибки;
б) если записи по решению данной задачи отсутствуют, то в таблице ставится прочерк; если записи есть, но вы считаете, что в них нет элементов правильного решения, то поставьте 0 баллов;
в) если решение данной задачи заслуживает 0 баллов, то можно эту оценку ставить сразу. За хорошие решения при первом просмотре оценку не ставьте, пока у вас не сформируется мнение об общем уровне решений данной задачи.
Жюри олимпиады необходимо обратить внимание на работы:
– в которых видно, что участник не знал данного материала, но в процессе решения олимпиадной задачи открыл его для себя, при этом он может выражать свои мысли в необычной форме;
– в которых участник искал оптимальное, в каком-либо смысле, решение. В неясных случаях обращайтесь к председателю жюри;
– проверьте снова все работы, где вы не поставили ноль или прочерк, и ставьте соответствующее количество баллов;
– для облегчения проведения апелляции запишите красными чернилами количество баллов и все замечания по письменному решению задачи.
Опыт членства в жюри олимпиад показывает нам, что необходимо осуществлять подготовку молодых кадров в состав жюри, для этого считаем целесообразным проводить предварительный инструктаж с членами жюри олимпиады, знакомить их с методическими рекомендациями по проверке, критериям оценки, способам решения и видам ошибок, допускаемых учениками при участии в олимпиадах.
Приведем решения заданий, предложенных участникам I, II туров городской олимпиады 2016–2017 учебного года для X и XІ классов для базового и профильного уровней.
Задания олимпиады для X класса базового уровня
Задача 1. Найдите все тройки действительных чисел (x, y, z), удовлетворяющих системе уравнений:
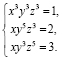
Решение: Рассмотрим любое из трех уравнений. Все три переменные в нем стоят в нечетных степенях. Это значит, что, либо все три числа x, y, z положительные, либо среди них два отрицательных и одно положительное. Причем при наличии отрицательных, если у них обоих сменить знак, мы получим положительное решение.
Отсюда следует, что достаточно найти все положительные решения. Меняя их знаки, получим и все остальные. Итак, считаем, что x > 0, y > 0, z > 0. Делим второе уравнение на первое, получим: y2 = 2x2, т.е. 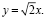 Делим третье уравнение на первое, получим: z2 = 3x2, т.е.
Делим третье уравнение на первое, получим: z2 = 3x2, т.е. 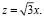 Подставляя все в первое уравнение, получим
Подставляя все в первое уравнение, получим
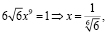
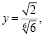
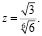
Итак, единственное положительное решение найдено. С учетом замечания про знаки получим еще три решения, т.е. всего четыре решения.
Ответ: 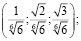
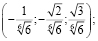
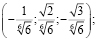
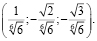
Задача 2. По неподвижному эскалатору человек спускается быстрее, чем поднимается. Что быстрее: спуститься и подняться по поднимающемуся эскалатору или спуститься и подняться по спускающемуся эскалатору? (Предполагается, что все скорости, о которых идет речь, постоянны, причем скорости эскалатора при движении вверх и вниз одинаковы, а скорость человека всегда больше скорости эскалатора). Условие и решение взято из задачной базы Самарского государственного университета [9].
Решение: Обозначим скорость эскалатора через v, скорости человека, поднимающегося и опускающегося по эскалатору, через v1, v2 соответственно, тогда v < v1 < v2. Длину эскалатора обозначим через v, тогда время движения по поднимающемуся эскалатору: t1 = ℓ/(v1 + v) – ℓ/(v2 – v). А по спускающемуся эскалатору t2 = ℓ/(v2 + v) – ℓ/(v1 – v). Вычислим разность t1 – t2 = ℓ/(v1 + v) + ℓ/(v2 – v) – ?/(v2 + v) – ℓ/(v1 – v) = 2ℓv(?/(v22 – v2) – ℓ/v12 – v2)).
По условию знаменатели обеих дробей положительны, причем первый больше второго, поэтому все выражение отрицательно. Вывод: t1 < t2.
Ответ: Быстрее спуститься и подняться по поднимающемуся эскалатору.
Задача 3 взята из издания [10]. Дан треугольник АВС, ∠B = 90 °. На сторонах АС, ВС выбраны точки Е и D соответственно такие, что АЕ = ЕС, ∠АDВ = ∠ЕDС (рисунок). Найти отношение СD:ВD.
Решение: Построим ∠ АВС, симметричный данному относительно стороны ВС. Точки А´, D, Е лежат на одной прямой, т.к. ∠АDВ = ?ЕDС. Следовательно, D – точка пересечения медиан А Е и СВ треугольника ∠ АА∠С, и делит их в отношении 2:1, считая от вершины.
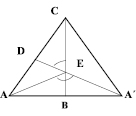
К задаче 3
Ответ: 2:1
Задания олимпиады для X класса углубленного уровня
Задача 1. На координатной плоскости нарисовано множество точек, заданное уравнением x = y2. Окружность радиуса 5 с центром в точке (11; 1) пересекает это множество в точках А, В, С, D. Докажите, что все эти точки А, В, С, D лежат на одной параболе, т.е. на кривой, заданной уравнением у = ах2 + bx + с, и найдите уравнение этой параболы.
Решение: Координаты точек А, В, С, D являются решениями системы
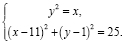 (1)
(1)
Раскрывая скобки во втором уравнении и подставляя у2 из первого, получим
х2 – 22х + 121 + х – 2у + 1 = 25⇒у = =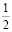 х2 –
х2 – 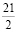 х +
х + 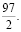 (2)
(2)
Поскольку уравнение (2) получено как следствие системы (1), любое решение системы (1) является решением уравнения (2). В частности, координаты точек А, В, С, D являются решениями уравнения (2), т.е. парабола, задаваемая уравнением (2), проходит через точки А, В, С, D.
Ответ: 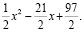
Задача 2. Доказать, что любое число 2n, где n = 3, 4, 5, … можно представить в виде 2n = 7х2 + у2, где х и у – нечетные числа.
Решение: Применим при решении метод математической индукции. Для n = 3 утверждение верно; пусть оно верно и для n = k: 2k = 7х2 + у2, где х и у нечетны. Рассмотрим две пары чисел:
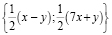
и
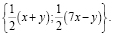
Для каждой пары усемеренный квадрат первого числа плюс квадрат второго дает 2k+1. Остается заметить, что в каждой паре стоят числа одной четности, а в разных – разной четности, поэтому числа одной из пар – нечетны. Условие и решение приводилось в [11].
Задача 3. Пусть а, b, c – стороны треугольника. Докажите неравенство: а3 + b3 + 3аbс > с3.
Решение: Используя неравенство треугольника а + b > c и то, что а2 – аb + b2 ≥ 0, получим цепочку неравенств:
а3 + b3 + 3аbс = (а – b)(а2 – аb + b2) + + 3аbс > а(а2 – аb + b2) + 3аbс = = с(а2 – аb + b2) > c•c2 = с3.
Задания олимпиады для XІ класса базового уровня
Задача 1. Решить уравнение 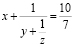 в целых положительных числах.
в целых положительных числах.
Решение задачи показано в [12]: любое число единственным образом представляется в виде суммы двух чисел, одно из которых – целое, а другое – неотрицательное и меньше единицы. Это сумма его целой и дробной части. Для 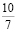 таким представлением будет
таким представлением будет 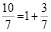 . Поэтому x = 1,
. Поэтому x = 1, 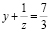 . Аналогично разложим
. Аналогично разложим 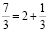 в сумму целой и дробной части. Получим y = 2, z = 3.
в сумму целой и дробной части. Получим y = 2, z = 3.
Ответ: x = 1, y = 2, z = 3.
Задача 2. Айбеку на 23 февраля подарили 777 конфет. Айбек хочет съесть все конфеты за n дней, причем так, чтобы за каждый из этих дней, кроме первого, но включая последний, съедать на одну конфету больше, чем в предыдущий. Для какого наибольшего числа n это возможно? Условие задачи аналогично условию задачи в [13].
Решение: Если в первый день Айбек съест a конфет, то за n дней он съест a + (a + 1) +…+ (a + n + 1) = 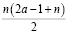 конфет.
конфет.
Значит, 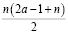 = 777. Следовательно n делит 2•777 = 1554. Так как 1554 = n(2a – 1 + n) >n2, то n < 40. Но максимальное число n меньшее 40 и делящее 1554 = 2•3•3•7•37 равняется 37. Случай n = 37 действительно возможен при a = 3.
= 777. Следовательно n делит 2•777 = 1554. Так как 1554 = n(2a – 1 + n) >n2, то n < 40. Но максимальное число n меньшее 40 и делящее 1554 = 2•3•3•7•37 равняется 37. Случай n = 37 действительно возможен при a = 3.
Ответ: n = 37.
Задания олимпиады для XІ класса углубленного уровня
Задание 1. Пусть a, b, c такие целые неотрицательные числа, что
28a + 30b + 31c = 365. Докажите, что a + b + c = 12. Данная задача приводилась в [13].
Решение: пусть a + b + c ≤ 11. Тогда 28a + 30b + 31c ≤ 31 (a + b + c) ≤ 11•31 = = 341 < 365, противоречие.
Пусть a + b + c ≥ 14, тогда 28a + + 30b + 31c ≥ 28(a + b + c) ≥ 28•14 = = 392 > 365, и этого быть не может. Осталось доказать, что: a + b + c не может равняться 13.
Пусть a + b + c = 13. Вариант a = 13, b = c = 0 не удовлетворяет условию: 28•13 + 30•0 + 31•0 = 364 > 365. Остается вариант a + b + c = 13, a < 13. В этом случае: b + c = 13 – a > 0 и 28a + 30b + + 31c = 28(a + b + c) + 2b + 3c ≥ 28•13 + + 2(b + c).
Первое слагаемое равно 364, второе – не меньше 2. Значит, сумма не меньше 366 и не может равняться 365. Следовательно, а + b + с = 12.
Задача 2. На координатной плоскости нарисовано множество точек, заданное уравнением x = y2. Окружность радиуса 5 с центром в точке (11; 1) пересекает это множество в точках А, В, С, D. Докажите, что все эти точки А, В, С, D лежат на одной параболе, т.е. на кривой, заданной уравнением у = ах2 + bx + с, и найдите уравнение этой параболы.
Решение: Координаты точек А, В, С, D являются решениями системы
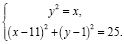 (1)
(1)
Раскрывая скобки во втором уравнении и подставляя у2 из первого, получим
х2 – 22х + 121 + х – 2у + 1 = 25⇒у = = 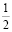 х2 –
х2 – 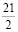 х +
х + 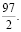 (2)
(2)
Поскольку уравнение (2) получено как следствие системы (1), любое решение системы (1) является решением уравнения (2). В частности, координаты точек А, В, С, D являются решениями уравнения (2), т.е. парабола, задаваемая уравнением (2), проходит через точки А, В, С, D.
Ответ: 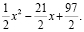
Задача 3. Рассмотрим все рациональные числа между нулем и единицей, знаменатели которых не превосходят n. Расположим их в порядке возрастания. Пусть 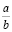 и
и 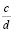 – какие-то два соседних числа (дроби несократимы). Доказать, что |bc – ad| = 1.
– какие-то два соседних числа (дроби несократимы). Доказать, что |bc – ad| = 1.
В [14] представлено следующее доказательство: можно считать, что 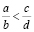 . Неравенство
. Неравенство 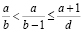 , которое выполняется при а + 1 ≤ b, показывает, что b ≠ d, т.е. знаменатели двух соседних дробей не могут быть одинаковыми. Докажем требуемое утверждение индукцией по n.
, которое выполняется при а + 1 ≤ b, показывает, что b ≠ d, т.е. знаменатели двух соседних дробей не могут быть одинаковыми. Докажем требуемое утверждение индукцией по n.
При n = 3 получим числа 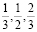 , для них утверждение легко проверяется. Предположим, что утверждение доказано для n – 1. При переходе от n – 1 к старому набору чисел добавляются некоторые числа вида
, для них утверждение легко проверяется. Предположим, что утверждение доказано для n – 1. При переходе от n – 1 к старому набору чисел добавляются некоторые числа вида 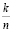 . Согласно сделанному выше замечанию два новых числа не могут быть соседними, поэтому
. Согласно сделанному выше замечанию два новых числа не могут быть соседними, поэтому
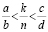 ,
,
где 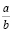 и
и 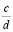 – соседние числа из старого списка.
– соседние числа из старого списка.
Нужно доказать, что оба числа A = kb – an и B = cn – kd равны 1 (ясно, что эти числа положительны). Предположим, что одно из них больше 1.
Тогда b + d < dB + dA = (bc – ad) n = n, поскольку bc – ad = 1 по предположению индукции. Неравенство 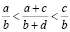 показывает, что числа
показывает, что числа 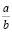 и
и 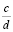 не могут быть соседними.
не могут быть соседними.
Приходим к противоречию, доказывающему, что |bc – ad| = 1.
Выводы
Cодержание олимпиадных задач соответствует логической структуре математической компетентности, а именно: компетентность, определенные умения, постановка задач на саморазвитие, следовательно, компетентностный подход реализуется при подготовке школьников к математическим олимпиадам. Так, процесс решения олимпиадных задач требует от учащихся сформированности ключевых и математических компетентностей третьего (креативного) уровня, поскольку специфика содержания таких задач проявляет все стадии познавательного процесса таксономии Блума. Оценивая олимпиадные работы, членам жюри важно соотнести содержание задач олимпиады с содержанием школьного образования, для этого необходимы критерии оценки олимпиадной деятельности учащегося. Считаем необходимым предварительное проведение методического инструктажа по проверке работ, способам решений и видам ошибок для членов жюри.

