В условиях реализации Концепции развития российского математического образования [1], введения в действие Федеральных образовательных стандартов (ФГОС) общего и высшего профессионального образования [2] стохастические знания становятся неотъемлемым компонентом инновационного содержания математического образования. Однако реализация стохастической линии связана по меньшей мере с тремя до конца не решенными проблемами:
– распределение содержания стохастического материала по уровням образования;
– преодоление кажущейся «оторванности» вероятностно-статистических понятий и фактов от «магистральной линии» курса математики;
– разработка технологий обучения стохастике, адекватных соответствующим уровням образования.
Обладая многолетним опытом как преподавания теории вероятностей и математической статистики, так и его научно-методического сопровождения, в настоящей работе авторы предлагают некоторые подходы к решению обозначенных проблем (не претендуя, разумеется, на их исчерпывающее решение).
Задачный подход. Стохастическая содержательная линия курса математики строится как объединение следующих взаимосвязанных составляющих: элементов комбинаторики, теории вероятностей, математической статистики. Одна из главных особенностей стохастической линии состоит в тесной связи отвлеченных понятий и структур с окружающим миром. Данной особенностью определяется технология изучения стохастики в школьном курсе. В качестве центрального звена технологии мы рассматриваем задачный подход – специально организованное и систематически осуществляемое обучение в виде разрешения разнообразных учебных задач. Задачный подход в применении к стохастике способствует развитию логического мышления, понуждает учащегося к поиску, самостоятельной добыче новых знаний. При этом существенно обогащается рефлексивный компонент математической деятельности: осознание учащимся своих результатов, критическая самооценка, укрепляется уверенность в себе, в своих возможностях («я могу!»), формируется настойчивость в движении к поставленной цели, аккуратность и сосредоточенность.
Можно говорить о трех этапах довузовской (школьной) стохастической подготовки соответственно уровням начальной, основной и старшей школ. Одним из основных требований к её результатам является готовность учащихся к дальнейшему освоению теории вероятностей, математической статистики и теории случайных процессов в вузовском курсе, чем обеспечивается преемственность и непрерывность стохастической подготовки.
Особенности этапа начальной подготовки. Начальный этап (1–4 классы школы) характеризуется преимущественно интуитивными, эмпирическими подходами к освоению соответствующих понятий, фактов и методов. Комбинаторные и вероятностно-статистические задачи основаны здесь на реальных сюжетах, имеют практическую направленность, что повышает интерес учащихся к математике. Решение таких задач позволяет учащимся накапливать опыт в выявлении математических закономерностей, выдвижении гипотез, способствует развитию вероятностной интуиции, логического мышления, комбинаторных способностей [3].
Среди комбинаторных принципов учащемуся вполне доступен формулируемый в общем виде принцип умножения. В части теории вероятностей центральными выступают понятия событий и их классификация. Введение понятий частоты, относительной частоты события и обнаружение свойства её устойчивости здесь связаны с сериями проводимых учащимися однотипных опытов. Альтернативным по отношению к статистическому подходу нахождения вероятности наступления случайного события служит умозрительный (априорный) подход, который реализуется в понятии классической вероятности. На начальном этапе подготовки классическая вероятность вводится как отношение числа благоприятных простейших исходов гипотетически проводимого опыта к общему числу его исходов, без формального уточнения требований к исходам. Задачный материал (см., например, [4]) может быть сгруппирован следующим образом:
– задания на систематизацию и визуализацию наблюдений (таблицы, диаграммы, схемы, дерево вариантов);
– комбинаторные задачи (перебор вариантов, комбинаторные формулы);
– вероятностно-статистические задания (относительная частота событий и обработка результатов эксперимента, вероятность случайных событий).
Среди технологических приёмов обучения отметим два следующих:
1) активизация деятельности учащихся в части построения примеров (примеры достоверных, невозможных и случайных событий и др.) и составление ими собственных задач, аналогичных решённым;
2) практические домашние задания; ограничимся здесь двумя примерами.
Задание 1. Накопите в течение недели монеты, выдаваемые вам в виде сдачи в буфете, магазинах, киосках и т.п. Подсчитайте количество монет и составьте вариационный ряд номиналов х монет (расположить их в таблице в порядке возрастания с указанием частот m). Запишите их относительные частоты w. Постройте полигон относительных частот (отметьте на координатной плоскости и соедините ломаной точки (x, w)).
Задание 2. Запишите меню вашего воскресного обеда. Перечислите все возможные варианты порядка подачи блюд (например, салат, компот, плов, суп). Сколько таких вариантов возможно?
На начальном этапе стохастической подготовки учащиеся отрабатывают умения выполнять арифметические действия, усматривают аналогию в задачах о вычислении вероятности события и вычислении процентов, используют таблицы и графики (полигон частот), что способствует установлению внутрипредметных связей в курсе математики.
Предлагаемый материал и приёмы его изучения служат пропедевтической базой для систематического освоения учащимися в курсе основной школы комбинаторных формул, различных моделей вероятности, вероятностей комбинированных событий, простейших статистических методов обработки выборочных данных.
Стохастика в основной и старшей школе. Центральными понятиями здесь являются понятия случайного события и его вероятности. Комбинаторные формулы, с нашей точки зрения, должны быть в первую очередь средством нахождения количества элементарных исходов опыта.
Последовательность введения основных понятий должна быть, по нашему мнению, следующей:
1) классификация событий и действиями над событиями (сложение, умножение), а также понятия, характеризующие «взаимоотношения» событий (полнота группы событий, события попарно несовместные, противоположные);
2) пространство элементарных исходов опыта;
3) классическая вероятность и её свойства;
4) статистическая и геометрическая вероятность.
В общем случае вероятность есть некоторая численная мера степени объективной возможности наступления события. Мы считаем поэтому, что рассмотрению конкретных моделей вероятностей (классической, статистической, геометрической) должен предшествовать соответствующий общий подход, а именно: за единицу «измерения» следует взять вероятность достоверного события; в этом случае невозможному событию естественно приписать вероятность, равную нулю, а случайные события во введённой шкале будут принимать значения от нуля до единицы. Рассматривая затем каждую из вышеперечисленных моделей вероятности, следует проверять наличие указанного шкалирования.
Вычисление классической вероятности мы предлагаем предварять «качественным анализом» исходов опыта, а именно проверкой их равновозможности, попарной несовместности и полноты группы.
Понятие геометрической вероятности открывает широкие возможности использования «внутрипредметной» связей с геометрией, способствует усилению мотивации к изучению геометрического материала. Так, моделируя вероятность как отношение площади области G, в которую должна попасть «случайно блуждающая» по области Е точка, к площади Е, можно построить серию задач, актуализирующих геометрические знания и умения. Так, примером использования подобия фигур может служить следующее задание.
Рекламный щит выполнен в форме равнобедренного треугольника, разделенного отрезком, параллельным основанию, на треугольник и трапецию, причем боковые стороны данного треугольника разделены в отношении 1:3, считая от вершины. Мальчик пускает солнечные «зайчики» на поверхность щита. Какова вероятность, что случайным образом пущенный «зайчик» попадет в трапецию?
Вычисление вероятностей «комбинированных» событий основано на теоремах сложения и умножения вероятностей. При их использовании отрабатываются понятия попарно несовместных событий, событий зависимых и независимых в совокупности, формируются приёмы нахождения вероятностей хотя бы одного из событий (как события, противоположного ненаступлению всех рассматриваемых событий), только одного из событий и др. При выборе способа решения задач полезно использование связей между операциями над событиями и соответствующими операциями над высказываниями (см. [5]).
Мы рекомендуем рассматривать задачи, в которых прослеживается связь стохастической линии с другими содержательными линиями (и отдельными темами) курса математики. Так, наличие связи с линией уравнений и неравенств может быть продемонстрировано учащимся на примере следующего задания.
Вероятность того, что только один из двух друзей сдаст ОГЭ по математике на отлично, равна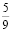 
. Для первого из друзей вероятность отличной оценки в два раза больше, чем для второго друга. Какова эта вероятность для каждого друга? Сколько решений имеет задача?
В процессе решения вводится параметр p, означающий соответствующую вероятность для второго друга; далее, строится уравнение вида
.
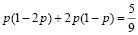Полученное квадратное уравнение имеет два различных корня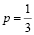 
и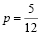 
; для первого друга получаем соответственно искомые вероятности равными 
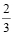или n. Задача имеет, таким образом, два различных решения.
В старших классах вышеуказанный стохастический материал может быть дополнен стандартными вероятностными схемами: схемой гипотез и схемой Бернулли. Здесь же могут быть введены понятия случайной величины, числовых характеристик дискретного распределения, теоретического распределения количественного признака генеральной совокупности и соответствующих ему эмпирических распределений, представленных выборками; далее, рассматриваются числовые характеристики эмпирического распределения (выборочные средняя, дисперсия, среднеквадратическое отклонение).
В процессе решения специально подобранных заданий учащиеся выявляют определённые внутрипредметные связи; при этом происходит актуализация соответствующих знаний и умений из других разделов курса математики. Приведём соответствующий пример.
Выстрелы по мишени выполняются до первого попадания. Вероятность попадания всякий раз равна p(0 < p < 1). Какова вероятность, что будет выполнено:
а) ровно k выстрелов (k = 1, 2, …);
б) не более n выстрелов (n = 1, 2, …).
Здесь имеется так называемое геометрическое распределение случайной величины Х – числа сделанных выстрелов. Вероятность попадания в мишень при k-ом выстреле определяется в виде Pk = (1 – p)k–1 p, k = 1, 2, …, 2, так что последовательность {Pk} представляет собою геометрическую прогрессию. Вероятность же выполнения не более n выстрелов определится в виде суммы Sn первых n её членов
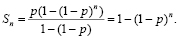
В старших классах учащимися уже накоплен некоторый опыт математической деятельности и, в частности, деятельности в области стохастики. Расширению и углублению данного опыта способствует приём использования в учебной практике так называемых кейс-заданий. В них могут быть одновременно актуализированы знания и умения в области комбинаторики, действий над событиями, вычисления вероятностей как непосредственно по определению, так и с помощью соответствующих теорем, а также анализа статистических данных с последующим прогнозированием зависимостей и др. Решение кейс-заданий способствует формированию системности стохастических знаний, умению использовать известные учащемуся факты и методы в новой ситуации, проводить комплексные исследования.
Теоретические упражнения («мини-теоремы») – эффективный технологический приём организации исследовательской деятельности учащихся. Сюда включаются: выдвижение гипотез, их подтверждение проведением соответствующего доказательства либо опровержение путём построения контрпримеров, решение стандартных задач в общем виде (когда вероятности заданы в форме параметров; см., например, приведённое выше упражнение на геометрическое распределение) и др. Приведём в качестве примеров также следующие упражнения.
1. Доказать, что
,
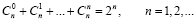где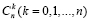 
– число сочетаний из n по k 
.
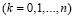2. Если геометрическая вероятность P(A) = 1, то означает ли это, что А – достоверно? Если P(A) = 0, то обязательно ли А – невозможное событие?
3. Доказать, что для любых двух событий A1 и A1 имеет место неравенство
.
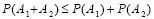4. Доказать, что выборочная средняя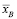 
принимает значения
,
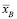
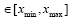где xmax и xmin – соответственно наибольшее и наименьшее значения вариант xk.
Выводы
Школьная (довузовская) стохастическая подготовка имеет ряд особенностей. Так, в основе распределения содержания материала по уровням образования лежат принципы наглядности, доступности, последовательности, систематичности, практической направленности, активности учащихся. Основным подходом в освоении элементов стохастики выступает задачный подход. При решении задач необходимо оптимально соотносить интуитивные, эвристические соображения с логическими рассуждениями, доказательностью. Такой оптимизации призваны способствовать предлагаемые выше технологические приёмы изучения стохастического материала: домашние задания практического характера, формулировка общих требований к понятию вероятности и проверка выполнимости этих требований на конкретных моделях, решение теоретических упражнений, позволяющее учащимся самостоятельно обнаруживать определённые математические закономерности в стохастике и др. Кроме того, указанные приёмы направлены на развитие логических умений учащихся, получение ими представлений о прикладном характере математических знаний, а также реализации внутрипредметных (внутриматематических) связей.