Высшее образование в современных условиях должно способствовать формированию специалистов широкого профиля с глубокими фундаментальными знаниями и обстоятельной практической подготовкой в конкретной отрасли промышленного производства или сельского хозяйства. Согласно требованиям ФГОС ВО компетенции выпускника сельскохозяйственного вуза как планируемый результат освоения образовательной программы включают подготовленность к научно-исследовательской деятельности, способность использовать математические методы при решении конкретных задач сельского хозяйства. В связи с этим разрабатываются специальные дисциплины, в рамках которых на высоком научном уровне изучаются соответствующие математические модели [1].
В Кубанском государственном аграрном университете имени И.Т. Трубилина для направления 20.04.02 «Природообустройство и водопользование» преподается дисциплина «Математическое моделирование процессов в компонентах природы». Целями её изучения являются: формирование профессиональных компетенций, обеспечение качественной подготовки квалифицированных специалистов в области рекультивации, мелиорации и охраны земель, эксплуатации водохозяйственных систем и оборудования на основе передовых инновационных технологий. В рамках дисциплины решаются практические задачи изучения гидрогеологических условий и прогноза их изменения под влиянием проектируемых мелиоративных решений, рационального использования и охраны подземных вод на мелиорируемых территориях с учетом их воздействия на окружающую среду [1, 2].
Дисциплина «Математическое моделирование» предполагает изучение специальных прикладных разделов математики, посвященных разработке математических моделей изучаемых процессов, теоретические основы которого закладываются на первом курсе при изучении высшей математики.
Задачей «Математического моделирования процессов в компонентах природы» является ознакомление студентов с наукой как сферой человеческой деятельности, овладение методологией научного поиска, изучение современных методов и средств научных исследований [3]. Необходимо научить студентов формулировать прикладные задачи, четко выявляя их математическую сущность, моделировать изучаемую ситуацию, отбрасывая все несущественные стороны, переводить математическую модель обратно в реальные рассматриваемые процессы и верно интерпретировать полученные математические результаты в контексте конкретной профессиональной деятельности. В рамках каждой дисциплины важно разработать практические рекомендации для проведения занятий с примерами из данной специальности. Примеры оживляют учебный процесс и вызывают интерес к углубленному изучению математики. Такой подход используется нами в учебном процессе при проведении практических (семинарских) занятий.
Прогноз изменения мелиоративной обстановки должен опираться на надежную количественную оценку процессов тепло- и массопереноса в ненасыщенных и насыщенных грунтах. Оценка может быть получена методами математического моделирования и вычислительного эксперимента с привлечением математической статистики. Этому разделу программы уделяем особое внимание [4].
Магистранты выполняют следующее задание: обработать результаты лабораторных определений коэффициента фильтрации по выборке из двадцати вариант, n = 20. Составить из них вариационный ряд [5]. Приведем кратко алгоритм решения.
Группируем данные. Вычисляем число интервалов N. Находим длину интервала ΔN. Зная длину интервала, находим для каждого интервала границы и окончательное их число. Составляем таблицу. Строим гистограмму и полигон частот. На оси абсцисс откладываем в масштабе интервалы значений коэффициентов фильтрации и для их центральных значений на оси ординат находим отвечающие им значения частот nm. Из построенной гистограммы видно, что данная статистическая совокупность асимметрична, гистограмма характеризует логнормальное распределение коэффициента фильтрации.
Следующее задание – построение логнормальной кривой распределения. Вычисляем логарифмы коэффициентов фильтрации, используя вариационный ряд. Проводим новую группировку данных. Результаты вычислений заносим в таблицы, строим гистограмму, из которой видно, что значения частот lgk распределены достаточно симметрично, что отвечает нормальному закону. Модальное значение отвечает интервалу с максимальной частотой. Значения среднего, медианы и моды практически совпадают, что может свидетельствовать о распределении lgk, близком нормальному закону.
Для построения интервальной оценки задаются доверительным уровнем (его обычно обозначают 2α) и ищут доверительный интервал [θ1, θ2]. Величина доверительного уровня стандартизована: обычно таблицы составлены для 2α = 0,05 (5%); 0,01 (1%) и 0,001 (0,1%). Выбор того или иного доверительного уровня связан с важностью проводимых исследований, точнее – с теми потерями, которые понесет общество, если мы ошиблись в своих выводах [6].
Построение доверительных интервалов основано на так называемом принципе «практической невозможности маловероятных событий»: если вероятность наступления события мала, то можно считать, что оно не наступит, и вести себя так, как будто это событие было бы невозможным событием. С этих позиций величина 2α и есть та граница, которая отделяет события практически невозможные от событий практически возможных. Если вероятность наступления события меньше 2α, то это событие можно считать практически невозможным и вести себя так, как если бы это событие никогда не наступало.
Эта трактовка и лежит в основе методики построения доверительных интервалов. Пусть мы имеем оценку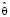 
, зависящую от выборки 
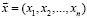. Можно найти
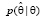, пользуясь методиками вычисления плотности вероятностей функций от случайных величин.
Возьмем доверительный уровень 2α и разделим его на две равные части 2α = α + α. Найдём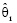 
из условия
.
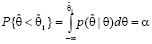Тогда это будет событие практически невозможное.
Аналогично, найдем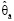 
из условия
.
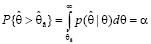Это будет также практически невозможное событие.
Событие, заключающееся в том, что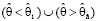 
, имеет вероятность 2α и поэтому также является практически невозможным событием.
Пусть теперь мы по выборке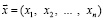 
нашли оценку 
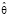. Каким значениям параметра θ она может соответствовать? Если считать события, имеющие вероятность наступления 2α, практически невозможными и поэтому не наступающими, то значения параметра θ, при которых наступившее событие будет практически возможным, будут лежать в интервале [θ1, θ2]. Это и будет доверительный интервал для параметра θ, соответствующий доверительному уровню 2α.
Для характеристики почвенного покрова как объекта сельскохозяйственного использования или предполагаемой мелиорации важна проверка независимости двух признаков.
Рассмотрим следующую задачу. Пусть имеется два случайных события А и В, которые наступают с вероятностями р(А) и р(В). Надо проверить следующую гипотезу Н0: р(АВ) = р(А) · р(В),
Н1: р(АВ) ≠ р(А) · р(В), которая утверждает, что события А и В независимы, а альтернатива – что они зависимы.
Пусть мы провели п опытов, в которых т11 раз появилась комбинация АВ, т12 раз – комбинация АВ, т21 раз – комбинация АВ и т22 раз – комбинация АВ. Это можно представить в форме таблицы, которая называется таблицей сопряженности признаков.
Таблица сопряженности признаков
|
В |
¯В |
|
|
А |
т11 |
т12 |
|
Ā |
т21 |
т22 |
Очевидно, что
т11 + т12 + т21 + т22 = п.
Пусть верна гипотеза Н0 и вероятности р(А) и р(В) нам известны. Тогда выражение для χ2 примет вид
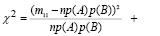
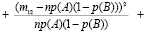
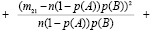
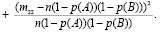
Но на самом деле р(А) и р(В) нам не известны. Поэтому заменим р(А) и р(В) их оценками. Так как в наших опытах событие А наступило всего т11 + т12 раз, а событие В – т11 + т21 раз, то
.
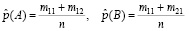Подставляя это в выражение для χ2, после громоздких преобразований можно получить, что
.
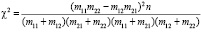Решающее правило выглядит так: если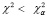 
, то принять гипотезу Н0, если 
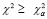, то отвергнуть гипотезу Н0. Величины 
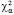находим по соответствующим таблицам.
Магистранты также знакомятся с непараметрическими критериями – по критерию Вилкоксона проверяют гипотезу об однородности выборок. Для ее проверки составляем из величин х1, х2, х3, …, хm и y1, y2, y3 …, yn один общий вариационный ряд, то есть располагаем в порядке возрастания их значений. В результате получаем последовательность из N значений (N = m + n). В качестве статистики для проверки гипотезы используем сумму рангов той выборки, объем которой меньше. Теоретические значения критерия находим из специальных таблиц в соответствии с объемами выборок и уровнем значимости.
Следующее задание для магистрантов - установить, можно ли считать доказанным влияние контролируемого фактора на рассматриваемый объект.
Решение этого вопроса связано со следующей математической моделью рассматриваемой ситуации. Считается, что величины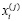 
можно представить в виде
,
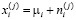где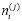 
– независимые одинаково распределённые случайные величины с нулевым математическим ожиданием и дисперсией σ2. Величина µi описывает влияние контролируемого фактора [7].
Проверка того, влияет ли контролируемый фактор на изучаемый объект, сводится к проверке следующей статистической гипотезы Н0: µ1 = µ2 = … = µs.
Принятие этой гипотезы означает, что влияние контролируемого фактора не доказано (действительно, ведь в этом случае µi не меняются!); если же эта гипотеза будет отвергнута, то влияние контролируемого фактора можно считать доказанным.
Для проверки этой гипотезы используем так называемый F-критерий. Согласно ему, следует вычислить величину
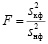
и сравнить это значение с пороговым значением Fα. Если окажется, что F ≤ Fα, то следует принять гипотезу Н0, то есть влияние контролируемого фактора нельзя считать доказанным. При выполнении противоположного неравенства F > Fα влияние контролируемого фактора можно считать установленным по уровню значимости α0. Пороговое значение Fα находится из таблиц F-критерия по выбранному уровню значимости α0, числу степеней свободы числителя f1 = s – 1 и числу степеней свободы знаменателя f2 = n – s.
Популярной оценкой меры зависимости двух случайных величин ξ и η является коэффициент корреляции, который определяется так
,
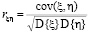где D{ξ} и D{η} – дисперсии случайных величин ξ и η, а cov(ξ, h) – их ковариация
.
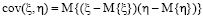Коэффициент корреляции является мерой линейной зависимости случайных величин дуг от друга.
Рассмотрим оценку коэффициента корреляции для нормальных случайных величин. Пусть имеются две случайные величины ξ и η. Проведено п опытов, в которых получили п пар измеренных значений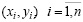 
. Оценка коэффициента корреляции, построенная по методу максимального правдоподобия, является асимптотически несмещенной и асимптотически эффективной. Для построения доверительного интервала для неизвестного коэффициента корреляции используют обходной путь через так называемое z-преобразование Фишера.
Рассмотрим величину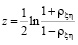 
.
Фишер показал, что распределение вероятностей этой величины очень хорошо аппроксимируется нормальным распределением с параметрами
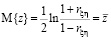
и дисперсией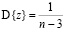 
, которая зависит только от объёма выборки п.
Задаемся доверительным уровнем 2α. Тогда можем сказать, что с вероятностью 1 – 2α будет выполнено неравенство
,
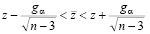где gα даётся таблицей:
|
2α |
0,05 (5%) |
0,01 (1%) |
0,001 (0,1%) |
|
gα |
1,96 |
2,58 |
3,29 |
Пусть
, 
.
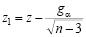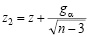Тогда с вероятностью 1 – 2α будет верно неравенство
,
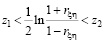разрешая которое относительно rξη, получим, что с вероятностью 1 – 2α будет верно неравенство r1 <rξη <r2, где
.
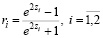Таким образом, величины r1 и r2 и есть границы доверительного интервала для неизвестного коэффициента корреляции rξη.
Немаловажную роль, на наш взгляд, играет усиление профессиональной направленности содержания дисциплины. Учебные задания, расчетно-графические работы целесообразно конструировать в тесной связи с различными реальными ситуациями и будущей профессиональной деятельностью студентов. Уже на уровне формулировки математической задачи можно с успехом использовать этот приём с целью адаптации восприятия излагаемого теоретического материала, повышения интереса магистрантов к изучаемой теме.
Профессионально направленное обучение математическим дисциплинам в вузе позволяет осуществлять глубокую фундаментальную и обстоятельную практическую подготовку магистранта для применения в конкретной отрасли сельского хозяйства, развивает его профессиональные навыки и компетенции, повышает его конкурентоспособность на кадровом рынке не только России, но и других мировых держав.