Организация городского и областного этапов республиканской олимпиады школьников по математике, представлена типовыми задачами, а последующие этапы, республиканский и международный, более сложные: «здесь много авторских задач исследовательского характера» [1]. И для достижения качественных результатов на олимпиадах всех уровней нужна систематическая подготовка их участников.
Раздел тригонометрия включен в «кодификатор основных тем олимпиадных заданий по математике» [2], и так как «…олимпиады выявляют качество знаний учащихся и ориентируют учителя, характеризуя уровень той предметной подготовки, которая считается высокой» [3, с. 5], то это могут быть как задачи повышенной трудности, соответствующие программе школьного курса, так и задачи, для успешного решения которых необходимы знания программы олимпиадной математики.
Цель и методы исследования: в статье мы исследуем возможности применения раздела тригонометрии в заданиях математических олимпиад. Для этого выполнен методический анализ содержания олимпиадных заданий по математике для IX–XI классов, изучены методические рекомендации по проведению республиканской олимпиады школьников в Кыргызстане, научная и учебно-методическая литература, касающаяся особенностей обучения тригонометрии, учащихся профильных и общеобразовательных школ.
Результаты исследования и их обсуждение
В исследовании О.В. Захаровой обучение тригонометрии в профильных классах рассматривается с позиций трех подходов: деятельностного, содержательного, личностно-ориентированного [4]. Расширяя область задач, решение которых требует знания раздела тригонометрии, автор предлагает включить в обучение задачи геометрического, геодезического, астрономического, физического содержания, выделяя при этом следующие их виды, показанные в табл. 1.
Таблица 1
Виды и цели обучения учебно-предметных задач тригонометрического содержания
|
Виды |
Цель обучения |
|
учебно-предметных задач тригонометрического содержания |
|
|
предметно-познавательные |
освоение знаний раздела тригонометрии |
|
практико-ориентированные |
демонстрация прикладной роли тригонометрии |
|
гуманитарно-ориентированные |
применение тригонометрии как научного инструмента для изучения природных процессов |
Анализируя тематику и содержание олимпиадных заданий по тригонометрии, мы определили в [5], что задания олимпиад в зависимости от уровня сложности, соответствуют типовой программе математики для общеобразовательных школ; программе математических кружков; программе школы олимпийского резерва.
Республиканская олимпиада 2017–2018 учебного года школьников Кыргызской Республики проводилась соответственно правилам ее организации [6]. Сформулируем принципы составления комплектов олимпиадных заданий для IX–XI классов общеобразовательных школ, требованиям которых должны удовлетворять задачи олимпиад:
1. Содержание олимпиадных заданий должно быть направлено на выявление способностей ученика применять знания в конкретных новых ситуациях, а не энциклопедичности знаний.
2. Олимпиадные задания должны включать элементы научного творчества, формирующие и развивающие способности участников генерировать новые идеи при решении.
3. Олимпиадные задания составляются на материале разделов математики: арифметики, алгебры, геометрии, тригонометрии, для IX–XI классов общеобразовательных школ, изученных в соответствующем классе к моменту проведения олимпиады.
4. В задания олимпиады необходимо включить задачи различного возрастающего уровня сложности.
5. Условия олимпиадных заданий должны быть корректными, не содержать термины и понятия, незнакомые учащимся соответствующего класса.
6. В зависимости от уровня олимпиады задания должны содержать задачи нового типа, при этом авторы задач считают, что «… для начальных этапов олимпиады нет необходимости в абсолютной новизне предлагаемых заданий» [7].
Включение тригонометрии в раздел олимпиадной математики А.Н. Марасанов обосновывает «наличием значительного числа внутрипредметных связей как внутри ее отдельных тем, так и между ними. Тригонометрия очень тесно связана с методом координат и с такими дисциплинами, как математический анализ, геометрия, алгебра» [8, с. 4], и конструирует систему задач соответственно принципам: преемственности; эвристического обучения; соответствия функциям задач; дифференциации. Перечисленные принципы объединяет принцип внутрипредметной связи [8, с. 7–8].
Роль тригонометрии в реализации принципа внутрипредметной связи в профильном обучении математике указана и в работе О.В. Захаровой: «Изучение тригонометрии в X–XI классах играет решающую роль в системе профильного обучения, так как универсальность математических методов позволяет в формальных понятиях алгебры, геометрии и математического анализа на уровне общенаучной методологии отразить связь теоретического материала различных областей знаний с практикой» [4].
Тригонометрия играет важную роль и в формировании умений школьника генерировать несколько идей решения задачи, это подчеркивает автор учебника по тригонометрии А.И. Новиков: «Многие задачи тригонометрии можно решать различными способами, не обязательно равноценными, но приводящими к искомому результату. Владение широким спектром решения задач является составной частью математической культуры учащегося» [9, с. 4]. Анализируя содержание заданий республиканской математической олимпиады школьников IX–XI классов Кыргызской Республики, проведенной в период 2014–2018 гг., мы выявили, что тригонометрические задачи составлены по следующим темам:
– Тождественные преобразования тригонометрических выражений.
– Тригонометрические функции числового аргумента, их графики и свойства монотонности, ограниченности, периодичности.
– Тригонометрические уравнения и неравенства.
Тригонометрия включена в программу обучения различных интеллектуальных конкурсов. Так, одно из решений задачи заочной олимпиады «Штурмуем Воробьёвы горы» в 2007 г. было основано на тригонометрической подстановке y = tg(x) [10]. В задания математической олимпиады Кенгуру в 2009 г. входила задача третьего уровня сложности: «Каково максимальное значение выражения sinαcosβ + sinβcosγ + sinγcosδ + sinδcosα для действительных α, β, γ, δ?» [11]. Задания олимпиады Ломоносова также содержат задачи на обратные тригонометрические функции.
Определенное место тригонометрия занимает и в построении содержания различных пособий и программ обучения олимпийцев. Так, в программу математики XI класса гуманитарно-математической школы А.С. Штерн включил изучение тем: «задачи на использование неравенства sinx < x; использование тригонометрических подстановок; геометрический смысл тригонометрических выражений; целые и рациональные значения тригонометрических функций; свойства тригонометрических функций» [10]. Учебное пособие для подготовки к единому государственному экзамену по математике содержит олимпиадные задачи на решение тригонометрических уравнений и неравенств; обратные тригонометрические функции [12]. Вышеперечисленное свидетельствует, что тригонометрия занимает важное место не только в школьных олимпиадах, но и в других интеллектуальных конкурсах. Исходя из этого, раздел тригонометрии включен в разработанную нами программу курса школы олимпийского резерва [3]. С учетом того, что: «Содержание курса направлено на расширение диапазона качественных характеристик усвоения обязательного уровня» [13], были определены цели обучения олимпиадной тригонометрии, показанные в табл. 2.
Таблица 2
Цели и требования по изучению олимпиадной тригонометрии
|
Раздел тригонометрии в программе школы олимпийского резерва |
||
|
Цель |
Требования к математической подготовке учащихся |
|
|
Знать |
Уметь решать |
|
|
– расширить и углубить знания школьного курса тригонометрии; – овладеть методами решения различных тригонометрических олимпиадных задач |
– основные формулы тригонометрии; – методы решения тригонометрических уравнений |
– тригонометрические уравнения и неравенства; – системы тригонометрических уравнений и неравенств |
Одним из факторов, положительно влияющих на уровень личностных образовательных достижений ученика в олимпиадах, считаем правильно построенную программу обучения: «Для решения задач олимпиадного характера школьникам недостаточно знаний, которые они получают на уроках, так как зачастую олимпиадные задачи выходят далеко за рамки школьной программы. Поэтому необходимо познакомить учащихся с теоретическими сведениями, которые очень часто применяются при решении олимпиадных задач, но не изучаются в школе» [5]. Кроме того, «задачи на доказательство и с элементами исследования, в частности тригонометрические уравнения с параметрами, являются средством развития навыков самостоятельной исследовательской работы», считает О.В. Захарова [4]. Электронный образовательный ресурс выступает основным инструментом реализации модели обучающей технологии по тригонометрии Н.И. Попова, основанной на теории поэтапного формирования умственных действий, и включает: «структурированный теоретический материал; практические задания; справочный материал; тесты для самоконтроля с указанием правильно и неправильно выполненных заданий; типовые упражнения и задачи для самостоятельного решения с ответами» [14]. При испытании модели при обучении студентов Марийского государственного университета автором выявлена «прямая зависимость развития интеллектуальных качеств учащихся от суммы накопленных ими конкретных приемов решения упражнений» [14].
Таким образом, основываясь на мнении исследователей, считаем необходимым формирование у школьников на обязательных уроках математики тех знаний методов преобразования тригонометрических выражений, решения тригонометрических уравнений и неравенств, которые будут способствовать овладению навыками решения олимпиадных задач. Так, участник олимпиады должен усвоить, что решение тригонометрических уравнений сводится к двум этапам: приведение уравнения к простейшему виду тригонометрического уравнения; решение полученного уравнения. И овладеть основными методами решения тригонометрических уравнений: «замены переменной t = tgx; исключения; разложения на множители; приведения к однородному уравнению относительно sinα и cosα; введения вспомогательного угла (уравнение вида asinx + bcosx = c); метод оценок и другие специальные приемы решения тригонометрических уравнений» [9]. Решение тригонометрических неравенств требует знаний всех групп тригонометрических формул, свойств неравенств, свойств единичной окружности, методов тождественных преобразований. А.И. Новиков считает необходимым ввести тригонометрические уравнения, содержащие радикалы, в программу обучения, указывая, что они: «…отличаются от других классов тригонометрических уравнений прежде всего необходимостью и важностью нахождения области допустимых значений уравнения» [9] и включает их в содержание обучения видов «тригонометрических уравнений:
– уравнений вида R(sin2nx, cos2kx) = 0; R(sinx ± cosx, sin2x) = 0;
– уравнения с радикалами и модулями;
– уравнения с дополнительными условиями. Отбор корней;
– уравнения со сложными тригонометрическими функциями» [9].
Далее покажем приемы решения разнотипных тригонометрических задач, предложенных учащимся X–XI классов на городских олимпиадах школьников г. Ош, демонстрирующих реализацию принципа внутрипредметной связи и комплексного применения математических знаний из нескольких разделов математики [15]. Решение задачи 1 для X класса основано на сочетании предметных знаний по геометрии и тригонометрии.
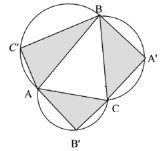
Рисунок к задаче 1
Задача 1. В остроугольном треугольнике ABC точки A', B', C' определяются следующим образом: точка A' является точкой пересечения продолжения высоты AD, опущенной на BC с полуокружностью, построенной во внешнюю сторону, причём BC является её диаметром (рисунок).
Аналогичным образом определяются точки B' и C'. Докажите, что 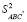 +
+ 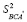 + +
+ + 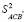 =
= 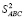 .
.
Доказательство:
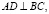
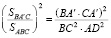 ;
; 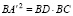 ;
; 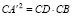 ;
;
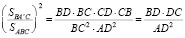 ;
; 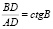 ;
; 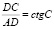 .
.
Тогда 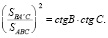
Требуемое соотношение примет вид
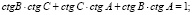
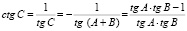 ;
;
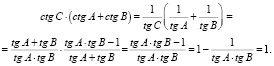
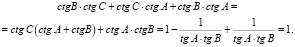
Ответ: 1.
Решение следующей задачи, автором которой является А.А. Заславский, требует комплексного применения знаний по геометрии и тригонометрии.
Задача 2. Тангенсы углов треугольника являются натуральными числами. Чему они могут быть равны? [16]
Решение: 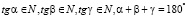 ,
, 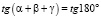 [16], пусть
[16], пусть 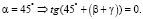
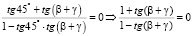 ,
,
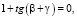 где
где 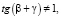 т.е.
т.е. 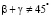 ,
, 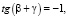
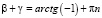 ,
, 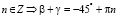 , n
, n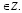
Если n = 1, то 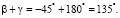 При α = 45 ° получили, что:
При α = 45 ° получили, что: 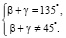
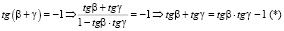 .
.
Подберем значения чисел к равенству (*) 2 + 3 = 2•3 – 1. Делаем вывод: tg β = 2,tg γ = 3.
Ответ: tgα = 1, tg β = 2, tg γ = 3.
Задача 3. Решить уравнение 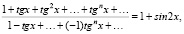
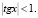
Решение: b1 = 1, b2 = tgx, b3 = tg2x, q = tgx,
1 + tgx + tg2x + …. + tgnx + ….= 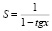 , 1 – tgx + …. +
, 1 – tgx + …. + 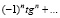 ;
;
b1 = 1, b2 = – tgx, bn = b1•q(n – 1); q = –tgx, b3 = tg2x, b3 = 1•tg2x,
1 + tgx + …. + 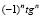 x + ….=
x + ….= 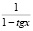 ,
, 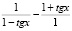 = 1 + sin2x,
= 1 + sin2x,
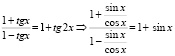 ,
, 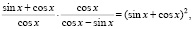
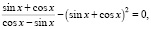
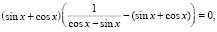
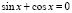 ,
, 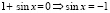 ,
,
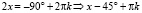 , т.е.
, т.е. 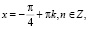
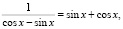
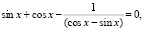
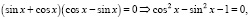
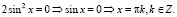
Ответ: πk, 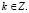
Следующая задача для X класса требует знаний свойств показательной функции.
Задача 4. Найдите наименьшее значение функции 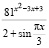 .
.
Решение: Показательная функция с основанием больше, чем единица, является возрастающей. Поэтому числитель примет наименьшее значение в точке минимума квадратичной функции x2 – 3x + 3. Этот минимум достигается в точке 1,5 и равен 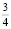 . Следовательно, наименьшее значение числителя равно 813/4 = 27. Так как точка 1,5 является также точкой максимума знаменателя исходной функции, то в ней достигается наименьшее значение функции
. Следовательно, наименьшее значение числителя равно 813/4 = 27. Так как точка 1,5 является также точкой максимума знаменателя исходной функции, то в ней достигается наименьшее значение функции 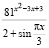 . Оно равно
. Оно равно 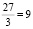 .
.
Ответ: 9.
Задача 5. Решить уравнение cos7x – sin7x = 1.
Решение: Так как функция cos7x четная, а sin7x – нечетная, исходное уравнение равносильно уравнению cos7(–x) + sin7(–x) = 1. Рассмотрев его вместе с основным тригонометрическим тождеством, получим систему: 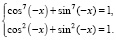
Ее решение (cos(–x); sin(–x)) не может состоять из чисел, модули которых меньше единицы. Поэтому возможны только решения cos(–x) = 1; sin(–x) = 0 и cos(–x) = 0; sin(–x) = 1. Следовательно, 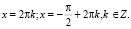
Ответ: 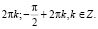
Задача 6 для XI класса. Найдите число положительных членов среди первых 2013 членов последовательности cos1 °, cos10 °, cos100 °, cos1000 °, cos10000 °, …
Решение: Так как cos1000 ° = cos(3•360 ° –80 °) = cos(–80 °) = cos80 ° > 0, то все последующие члены последовательности положительны. Докажем это.
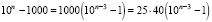 для всех n > 3.
для всех n > 3.
Выражение в скобках делится на 9, так как оно составлено из девяток. Следовательно, 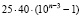 кратно 360, так как 9•40 = 360. Поэтому,
кратно 360, так как 9•40 = 360. Поэтому, 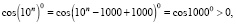 для всех n > 3.
для всех n > 3.
Ответ: 2012, т.е. все числа данной последовательности, кроме cos100 °.
Одной из целей дисциплины «Внеклассная работа по математике и методика решения олимпиадных задач» бакалавров группы МК(б)-1-14Р факультета «Математика и информационные технологии» ОшГУ являлось формирование компетентности студентов в области олимпиадной тригонометрии. В задания диагностического тестирования знаний студентов методов решения олимпиадных задач по математике, проведенного 16 апреля 2018 г., был включен перечень учебных элементов: знание формул тригонометрии, методов решения тригонометрических уравнений; умения решать тригонометрические олимпиадные задачи. В результате получены показатели качественной – 47 % и абсолютной – 87 % успеваемости обученных студентов.
Выводы
На основании изложенных в статье мнений авторов научных исследований и методических работ мы делаем вывод, что включение тригонометрии в олимпиадную тематику в немалой степени основано на возможностях комплексного применения знаний всего курса математики при решении тригонометрических олимпиадных заданий.
Повышение уровня сложности заданий республиканской олимпиады по математике показывает необходимость обучения учащихся решению олимпиадных задач, содержание которых построено на тригонометрическом материале, на занятиях математического кружка и школы олимпийского резерва, что требует от учителя выхода за рамки школьной программы и демонстрации новых методов решения тригонометрических задач.
Активизация личностной потребности ученика в успехе позволит учителю, осуществляющему олимпиадную подготовку, ориентировать образовательный процесс на его академические достижения.

