Развитие науки и техники делает необходимым достижение новых результатов обучения, требующих применения инновационных образовательных технологий. Современный процесс обучения должен быть ориентирован на развитие навыков самообразования и саморазвития, креативности мышления, умения формулировать цели и решать научно-практические задачи [1]. Дидактика образования должна быть сконцентрирована на необходимости привития навыков поиска и систематизации информации, построения логики рассуждений, умения четко формулировать задачу и методы, необходимые для ее решения, согласовывая их с существующими рыночными реалиями [2]. Поэтому вероятностные дисциплины (теория вероятностей, математическая статистика, теория случайных процессов) являются одними из наиболее востребованных математических дисциплин и изучаются бакалаврами, специалистами и магистрантами большинства направлений подготовки [3]. Отметим особый статус вероятностных дисциплин, идеология и дидактика преподавания которых существенно отличаются от других дисциплин математического цикла [4]. Как известно, теория вероятностей является аксиоматической теорией, такое построение дисциплины трудно для восприятия студентами технического направления, не имеющих достаточной подготовки по таким дисциплинам, как математическая логика, функциональный анализ, теория графов [5, 6].
Целью настоящего исследования является проектирование инновационных дидактических приемов, нацеленных на раскрытие междисциплинарных связей и обеспечивающих повышение качества подготовки студентов-инженеров по вероятностным дисциплинам.
Основные трудности при изучении дисциплин вероятностного цикла
Основные сложности при изучении математических дисциплин хорошо известны, пути их преодоления подробно рассмотрены в ряде работ, например в [3, 7, 8]. Дополнительно в качестве причин недостаточной успеваемости отметим плохую мотивированность, а также страх перед изучением STEM-дисциплин (Science – наука, Technology – технология, Engineering – инженерия, Mathematics – математика) [9]. У студентов технического направления подготовки часто сильно выражен страх именно перед математическими дисциплинами. Остановимся на основных известных трудностях, дополнительно возникающих при обучении вероятностным дисциплинам.
При изучении дисциплин вероятностного цикла часто возникают сложности, связанные с громоздкостью формул и «плохими числами» при анализе реальных явлений, необходимостью большого объема рутинных вычислений [6]. Часто при их выполнении студенты теряют логику рассуждений, не видят связи между постановкой задачи и полученным результатом [4]. Также в инженерной практике нередко возникают задачи, аналитическое решение которых часто бывает практически нереализуемым или требующем слишком большого времени решения и/или затрат. Поэтому навыки численного решения и моделирования приобретают особую значимость в рамках системного подхода к решению задачи.
Кроме того, зачастую отдельная часть потока не в состоянии провести математические выкладки в принципе в силу отсутствия у них необходимых навыков или же из-за забывания материала, пройденного на первых курсах. Это становится особенно очевидным при обучении магистрантов, группы которых очень разнородны по своему составу и полученному ранее образованию [5]. Поэтому при решении задач могут быть использованы персональные компьютеры, планшеты или смартфоны, на которые установлены специальные комплексы программ. Согласно [10], выбор той или иной технологии в равной степени должен быть обусловлен наличием определенных материальных ресурсов и предполагаемых результатов обучения. Использование цифровых технологий оказывает существенное влияние не только на процесс обучения, но и на восприятие изучаемой дисциплины и ее законов.
Несмотря на то, что вероятностные дисциплины являются необходимыми элементами математического образования возникают ситуации, когда отсутствующие базовые знания теории вероятностей не позволяют студентам успешно освоить математическую статистику или теорию случайных процессов [4–6].
Важно отметить, что для успешного анализа случайных явлений необходимы обширные междисциплинарные знания, включающие фундаментальные дисциплины математического цикла. Инновационные методы обучения, рассматриваемые в том числе в настоящем исследовании, направлены на раскрытие этих связей, а также на максимальную визуализацию рассматриваемых схем и явлений.
Известно, что программирование является одной из самых сложных дисциплин для студентов, не изучавших его ранее, например, в школе, а также требует значительного количества времени [11]. Кроме того, ввиду большого их разнообразия бывает затруднительно обеспечить знание одного и того же языка на большом потоке, состоящем из групп разных специализаций подготовки. Более удобным будет использование программ компьютерной математики, таких как Mathematica, Matlab, Mathcad, основы которых могут быть изучены гораздо быстрее.
Дополнительным преимуществом систем компьютерной математики является возможность создать шаблоны решения для типовых задач [4, 6, 12], могут быть найдены полные аналитические решения за счет варьирования исходных данных, ведущих к изменению промежуточных и конечных результатов. Также эти программные комплексы удобны для визуализации полученных зависимостей. Интерактивные шаблоны и методические преимущества их использования рассмотрены в [6, 12].
Описание предлагаемой методики раскрытия междисциплинарных связей
Методический комплекс дисциплины [4], традиционно состоящий из материалов лекционного курса и семинарских занятий, вариантов домашних заданий и контрольных работ по одному или нескольким учебным модулям, предлагается дополнить инновационными учебными материалами – комплектом презентаций и интерактивных шаблонов, иллюстрирующих решаемые задачи и основы выборочного метода.
Для студентов-инженеров особенно важно подчеркивать связь между реальными физическими явлениями и результатами, получаемыми в теории, решать задачи профессиональной направленности. Например, когда в теории вероятностей изучают понятие медианы, необходимо апеллировать к выводу формулы для периода полураспада. Математическая формулировка закона больших чисел также с трудом воспринимается подавляющим большинством слушателей, однако если напомнить о его связи с измерениями физических параметров, которые проводились в том числе на лабораторных работах по физике, то смысл закона становится понятным.
При изучении основных моделей в теории вероятностей, математической статистике и теории случайных процессов мы предлагаем действовать по следующей схеме:
1) объяснять, откуда появилась конкретная математическая модель;
2) разбирать ее свойства и их значение для практики;
3) подробно объяснять, какие реальные явления описывает данная модель и при каких условиях;
4) обсуждать возможные способы обобщения, включая то, в каких случаях это необходимо и к каким дополнительным трудностям ведет.
Создаваемые электронные средства обучения должны дополнительно иллюстрировать каждый из приведенных пунктов.
Для проектирования таких электронных средств обучения для студентов-инженеров удобно использовать системы компьютерной математики (Matlab, MathCad, Mathematica). Одним из преимуществ этих систем является традиционная математическая форма представления функций и удобные средства визуализации. Основные принципы и методы обучения с использованием этих технологий приведены в [4, 8, 12]. Использование таких программных комплексов сводит к минимуму необходимость рутинных вычислений, позволяет получать решения для реальных явлений, не прибегая к аналитическим выкладкам. Дополнительным преимуществом является то, что при составлении банка заданий отпадает необходимость в ручном отборе вариантов с хорошими числами. Как известно, обновление банка заданий является необходимым условием достижения высоких результатов обучения [3].
Наряду с создаваемыми материалами для демонстрации необходимо включение в образовательный процесс интерактивных шаблонов [12]. Особенно важным представляется то, что при их использовании студенты могут самостоятельно проводить дополнительные опыты по моделированию с целью установления новых свойств или проверки уже установленных [6].
Рассмотрим пример применения предлагаемой методики и используемых материалов.
Пример. Найти функцию распределения дальности полета снаряда в пустоте, выпущенного под углом α к горизонту с начальной скоростью v0, предполагая, что а) угол α распределен равномерно в интервале (0; π/2); б) угол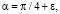 
где ε – случайная ошибка, распределенная нормально со средним квадратичным отклонением π/36; в) угол 
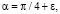где ε – ошибка округления, распределенная равномерно со средним квадратичным отклонением 
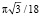. Провести численное моделирование дальности полета во всех трех случаях при v0 = 100 м/с, объем выборки взять равным n = 5. Провести качественное и количественное сравнение результатов для разных распределений.
Решение. Разобьем решение на несколько частей, к каждой из которых приведем список знаний, умений и навыков, приобретаемых студентами при решении.
Часть 1. Аналитическое решение. Воспользуемся известными формулами для времени Т, дальности S и высоты H полета:
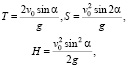(1)
где g – ускорение свободного падения. Тогда функция распределения случайной величины S может быть найдена из следующего равенства
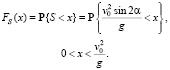(2)
Уравнение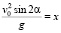 
имеет два решения при 
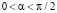, которые мы обозначим
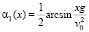
и
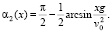(3)
Решая последнее неравенство в (2) относительно α, получаем связь между функциями распределения α и S:
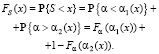(4)
При решении первой части задачи студенты приобретают знания таких понятий, как функция распределения, обратная функция, функция от случайной величины; умения выводить закон распределения скалярной функции от случайной величины из ее закона распределения; вспоминают навыки решения тригонометрических неравенств. Демонстрируется связь решения задачи по теории вероятностей с формулами из физики (1) и знаниями математического анализа (3).
Часть 2. Аналитическое решение с использованием системы Mathematica. Дальнейшие выкладки проведем в системе Mathematica, дабы избежать рутинных вычислений.
Зададим распределения из пунктов а)–в) и соответствующие им функции распределения по формуле (4). Код системы Mathematica приведен ниже.
S[v0_,α_]:=v0^2 Sin[2α]/g; H[v0_,α_]:=(v0 Sin[α])^2/(2g);
Dist1=UniformDistribution[{0,π/2}]; Dist2=NormalDistribution[π/4,π/36];
Dist3=UniformDistribution[{-(π/(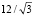
))+π/4,π/(
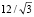)+π/4}];
g1[v0_,x_]:=ArcSin[(g x)/v02]/2; g2[v0_,x_]:=π/2-ArcSin[(g x)/v02]/2;
F1[v0_,x_]:=CDF[Dist1,g1[v0,x]]+1-CDF[Dist1,g2[v0,x]];
F2[v0_,x_]:=CDF[Dist2,g1[v0,x]]+1-CDF[Dist2,g2[v0,x]];
F3[v0_,x_]:=CDF[Dist3,g1[v0,x]]+1-CDF[Dist3,g2[v0,x]];
Вычислим числовые характеристики для указанных законов:
M1=Table[Integrate[S[v0,u]PDF[Dist,u],{u,-∞, ∞}],{Dist,{Dist1,Dist2,Dist3}}];
M2=Table[Integrate[S[v0,u]^2 PDF[Dist,u],{u,- ∞,∞}],{Dist,{Dist1,Dist2,Dist3}}];
D1=FullSimplify[(M2-M1^2)];
Tab1=TableForm[{{"Dist1","Dist2","Dist3»},M1,D1}]
В результате получим таблицу значений числовых характеристик, однако в силу ее громоздкости в статье ее не приводим. Вид числовых характеристик в общем случае достаточно громоздок, однако нам удалось их вычислить, не прибегая к рутинным вычислениям. Сразу же можно получить и численные значения. В качестве дополнительной задачи можно предложить желающим провести все выкладки аналитически для получения дополнительных рейтинговых баллов.
Построим графики найденных функций распределения (рис. 1).
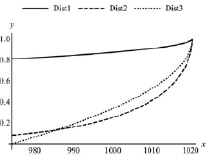
Рис. 1. Графики функций распределения для законов а), б) и в)
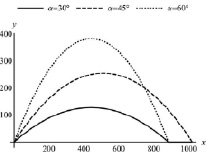
Рис. 2. Графики траекторий полета снаряда при различных α
g=9.8; v0=100; N[Tab1]
Plot[{F1[v0,x],F2[v0,x],F3[v0,x]},{x,S[v0,π4π/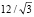
],S[v0,π4]},
PlotLegends>Placed[{"Dist1","Dist2","Dist3"},Above]]
При решении второй части задачи студенты приобретают знания способов задания основных законов распределения в системе Mathematica, вида и формы функции распределения, а также навыки по вычислению числовых характеристик случайных величин, вспоминают понятия интеграла (собственного и несобственного), а также техники интегрирования. Здесь также необходимо отметить, что вычислительный аспект задачи базируется на знании математического анализа.
Часть 3. Численное моделирование. Зададим функцию, определяющую траекторию полета, и построим ее график при нескольких значениях α.
y[x_,v0_,α_]:=Piecewise[{{a x (S[v0,α]-x)/(S[v0,α] v0 Cos[?]),0<x<=S[v0,α]}}];
y1[x_,v0_,α_]:=y[x,v0,α]/.Solve[y[S[v0,α]/2,v0,α]==H[v0,α],a];
Plot[Evaluate@Table[y1[x,v0, α],{ α,{π6,π4,π3}}],{x,0,v0^2π},PlotLegends>
Placed[Table["α="<>ToString[180απ]<>"°",{α,{π6,π4,π3}}],Above]]
Приведем моделирование значений дальности полета и построение соответствующих графиков только для случая а), так как случаи б) и в) отличаются только заменой распределения. Графики траекторий представлены на рис. 3.
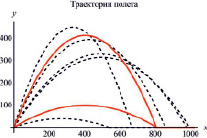
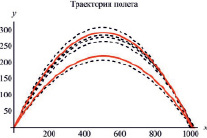
а) б)
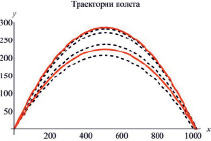
в)
Рис. 3. Графики смоделированных траекторий полета (пунктирные линии) и возможные траектории, соответствующие средней дальности полета (сплошная линия) для случаев а), б) и в) соответственно
s1=RandomVariate[Dist1,5];
s2=Table[S[v0,s1[[j]]],{j,1,5}];
m2=Mean[Table[S[v0,α],{α,s1}]];
Show[Plot[Evaluate@Table[y1[x,v0,α],{α,s1}],{x,0,S[v0,π/4]},AxesLabel->{"x","y"},
PlotLabel->"Траектории полета", PlotStyle->Dashed, PlotTheme->»Monochrome»],
Plot[y1[x,v0,α]/.Solve[S[v0,α]==m2,?],{x,0,S[v0,π/4]}, PlotStyle->{Thick,Red}],
Plot[y1[x,v0,α]/.Solve[S[v0,α/2-?]==m2,α],{x,0,S[v0,π/4]}, PlotStyle->{Thick,Red}]]
При решении третьей части задачи студенты приобретают знания об основных принципах выборочной теории, вычислении выборочных характеристик и их свойствах; навыки по моделированию в системе Mathematica, вычислению выборочных характеристик; навыки качественного и количественного сравнения полученных результатов.
Данный пример демонстрирует следующие основные характеристики предлагаемой методики обучения:
1) раскрытие междисциплинарных связей;
2) практическая направленность рассматриваемых задач;
3) использование систем компьютерной математики как средства для проведения рутинных выкладок и визуализации.
Кроме того, возникает большое количество дополнительных задач различной сложности, которые можно предложить для самостоятельной работы. Это очень важно в рамках организации модульно-рейтинговой системы контроля успеваемости [7].
Важно отметить, что предлагаемые средства обучения применяются не обособленно, а дополняют традиционный методический комплекс дисциплины. Например, при обучении в рамках модульно-рейтинговой системы [7] возможно получение дополнительных баллов для студентов, активно использующих интерактивные шаблоны, или тех, кто предложил или модифицировал подобные шаблоны самостоятельно. Кроме того, возможно выполнение определенных заданий по командам, повышающее мотивированность за счет соревновательного процесса [13]. Необходимы также коллективное обсуждение и верификация результатов, получаемых отдельными группами. При этом обоснованная критика или, наоборот, обоснование правильности решения должно также поощряться дополнительными баллами.
Результаты исследования и их обсуждение
В работах [3, 7, 13] установлено, что использование средств обучения, основанных на системах компьютерной математики, имеет положительное влияние на результаты обучения по дисциплинам математического цикла. Настоящее исследование позволяет сделать аналогичный вывод относительно использования инновационных дидактических методов, раскрывающих междисциплинарные связи посредством использования систем компьютерной математики.
Остановимся на важных способах достижения более высоких результатов обучения. Одним из основных факторов, влияющих на уровень успеваемости, является мотивированность. Низкий уровень мотивированности на достижение заявленных результатов обучения может быть вызван как недостатком профессиональных ориентации и адаптации на этапе выбора специальности и учебы на первых курсах университета [7], так и несовпадением между восприятием уровня своих знаний и действительного уровня подготовки по математике. В [4] установлено, что те студенты, у которых наблюдался баланс между этими двумя факторами, были более мотивированы и готовы потратить дополнительное время на преодоление трудностей, возникающих при решении задач. В [14] описана структура мотивации и предложена регрессионная модель, связывающая отношения разных компонент мотивации (гендер, образовательная программа и предыдущие успехи) у группы студентов, изучающих курс анализа данных, в котором компьютерные технологии интегрированы в образовательный процесс. Оказалось, что мотивированность является одним из важнейших факторов, влияющих на результаты обучения.
Цель любых образовательных технологий состоит в том, чтобы повысить заинтересованность и вовлеченность студентов в процесс обучения. В [14, 15] установлено, что возможно использование информационных технологий, в том числе систем компьютерной математики, в качестве инструмента для решения этой задачи. Наше исследование показывает, что таким инструментом выступают в том числе интерактивные шаблоны, созданные при помощи систем компьютерной математики.
Также новые информационные технологии позволяют индивидуализировать процесс обучения, подстраивая методы под способности и интересы каждого отдельного студента. Одновременно они позволяют контролировать уровень достижений, мотивируя и студента, и преподавателя к достижению поставленных целей обучения.
Заключение
Предложен дидактический прием преподавания дисциплин вероятностного цикла с использованием инновационных учебных материалов (демонстрационные материалы и интерактивные шаблоны для решения задач), подготовленных с помощью систем компьютерной математики для студентов-инженеров. Предлагаемые методы обеспечивают визуализацию полученных результатов, сокращают объем проводимых рутинных вычислений, раскрывают междисциплинарные связи вероятностных дисциплин с другими дисциплинами математического и профессионального циклов. Они могут применяться в рамках модульно-рейтинговой системы контроля учебного процесса, представляя дополнение методического комплекса дисциплины, повышая заинтересованность студентов и мотивируя из на достижение высоких результатов обучения. В рамках рассматриваемого дидактического приема возможно использование различных методов обучения, в том числе соревновательного и игрового.