Любая работа трудна в выполнении без достаточной мотивации. Это относится и к процессу обучения. При рассмотрении проблематики отсутствия мотивации у студентов в процессе изучения предметов математического цикла можно выделить следующие задачи:
– укрепить в сознании студента связь математических дисциплин с другими предметами, предусмотренными образовательным стандартом по его специальности;
– дать прочувствовать связи непосредственно самих предметов математического цикла, а также мотивировать студента для более углубленного изучения предмета;
– помочь осуществить связь математики с окружающей действительностью, другими жизненными проблемами.
Одно из решений поставленных задач – это вовлечение студента в научную работу, в которой используется изученный в рамках предмета математического цикла материал. При написании научной статьи, тезисов доклада для студенческой конференции у учащегося возникает потребность в использовании дополнительной литературы по предмету, углубленном изучении тематики вопроса.
Но самое главное при решении поставленных задач – таким способом учесть личные предпочтения студента при выборе темы исследования. Только в этом случае возникнет дополнительная мотивация и интерес.
Цель исследования: проверить, как вовлечение учащегося в научную деятельность повлияет на решение поставленных выше задач.
Материалы и методы исследования
В данном эксперименте участвовали пять студентов с различными личными интересами: учащиеся, у которых было повышенное внимание к предмету, связанному с их профессиональной деятельностью, студентка, у которой было желание более глубоко изучить математические дисциплины, студентка, интересы которой выходили за рамки обучения в университете. Исследование длилось два года, в ходе которых каждый студент был вовлечен в научную деятельность с учетом их пожеланий.
Результаты исследования и их обсуждение
Пример 1
Студент направления подготовки «информационные системы и технологии», обучающийся по профилю «информационные системы и технологии», имеет оценку «отлично» по предмету «языки программирования высокого уровня». Успевать по данной дисциплине могут только учащиеся с хорошо развитым алгоритмическим мышлением. Перевод задачи на язык схем и символов не составляет для них труда.
Стоит предположить, что у такого студента не могут не вызывать интерес предметы математического цикла. Однако часто в процессе обучения способный ученик уделяет больше внимания предмету, который больше нравится. Это влечет за собой поверхностное изучение материала и отсутствие владения техникой решения задач, что в дальнейшем может привести к затруднению ведения видов деятельности, к которым должен быть готов студент, освоивший программу бакалавриата по направлению 09.03.02: проектно-конструкторская и научно-исследовательская.
Цели и задачи: помочь студенту осуществить связь между предметами «языки программирования высокого уровня» и «математика»; поставить перед учащимся задачу, которую он мог бы использовать в своей дальнейшей научной деятельности.
Решение:
В рамках предмета «математика» у студентов первого курса направления подготовки «информационные системы и технологии» изучается тема «Решение систем линейных алгебраических уравнений методом Гаусса». Данный метод широко применим для решения прикладных задач в различных областях.
Студенту была предложена совместная научная работа по теме: особенности преподавания предметов математического цикла у студентов специальности «информационные системы и технологии» (рис. 1) [1].
Сначала была поставлена задача и произведен научный эксперимент: студенту нужно было запрограммировать изученный на занятии алгоритм.
Будем решать систему: 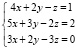 .
.
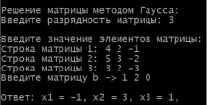
Рис. 1. Пример работы программы
Далее результаты были оформлены в виде научной статьи, в ходе написания которой учащийся научился составлять план публикации, осуществлять её оформление.
Вывод:
Во время данной работы студент познакомился с дополнительной литературой по алгебре и численным методам, что обязательно пригодиться в дальнейшем, попробовал себя в роли настоящего программиста, наглядно смог проследить связь алгебры с языками программирования.
Пример 2
Часто студенты более старших курсов, вовлеченные в научную деятельность преподавателями кафедр специализации, сталкиваются с проблемой применения полученных математических знаний в решении поставленных научно-прикладных задач.
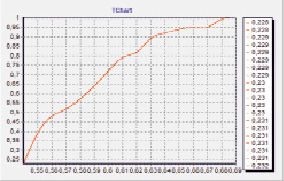
Рис. 2. Эмпирическая зависимость между деформацией модуля и вероятностью увеличения потерь
Студентка направления подготовки «Оптические системы связи» со своим научным руководителем занималась проблемой деформации кабеля в неблагоприятных погодных условиях. Была необходимость в построении математической модели по отысканию зависимости между деформацией модуля оптического кабеля и вероятностью увеличения потерь в нём.
Цели и задачи: помочь построить математическую модель поставленной прикладной задачи; помочь разобраться, какую часть из полученного математического образования следует применять для решения полученной математической задачи; помочь научиться читать математическую литературу, соответствующую поставленной задаче.
Решение:
Студентке была предложена для чтения и изучения дополнительная математическая литература [2]. Чтобы учащейся было легче ориентироваться в данных учебниках, были указаны разделы и номера страниц, на которые следует обратить особое внимание.
После была построена математическая модель и на основе формулы наименьших квадратов найдена зависимость
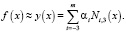
Для дальнейшего исследования надо было полученную зависимость представить графически (рис. 2). Поэтому была написана программа на языке C++.
Результаты работы были оформлены в виде научной статьи [3].
Вывод:
За время выполнения данной работы студентка познакомилась с дисциплиной «численные методы», не предусмотренной учебным планом для её специальности.
Кроме того, она научилась читать математическую литературу и использовать на практике знания, полученные при изучении предметов математического цикла, самостоятельно разрабатывать математическую модель из результатов исследования.
Пример 3
Часто у студентов не технических специальностей возникают вопросы, с какой целью им следует изучать математические дисциплины.
Студентка направления «Прикладная информатика», обучающаяся по профилю «Прикладная информатика в экономике», хорошо успевала и была заинтересована в специальных предметах экономического цикла. При этом её очень интересовало, зачем студентам-экономистам столь углубленно, с её точки зрения, изучать математический анализ.
Цели и задачи: помочь осуществить связь между предметами специального (экономического) цикла и математическими предметами; помочь научиться доводить экономическую модель до математической задачи; помочь разобраться в специальной математической литературе для студентов экономических специальностей.
Решение:
Студентке была предложена научная работа на тему «применение интегралов в экономике».
Сначала нужно было изучить специальную литературу [4], потом поставить экономическую задачу и решать её математическими методами, изучаемыми в рамках предмета.
Например, с помощью интегрирования можно искать излишек товара (рис. 3) [5]: 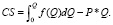
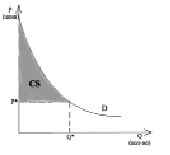
Рис. 3. Потребительский излишек товара
Результаты были оформлены в виде научной публикации.
Вывод:
При написании данной работы у студентки четко сформировалась связь между специальными, гуманитарными предметами и математикой. Кроме того, она научилась не бояться читать математическую литературу [5], что обязательно пригодится ей в дальнейшем.
Пример 4
Студентка направления подготовки «Управление инновациями» – выпускница гимназии с углубленным изучением математики. Некоторые темы предмета «математика» ученики таких школ изучают в рамках школьной программы. По этой причине выпускники математических гимназий часто запускают изучение математики в вузе, мотивируя данный факт тем, что они это уже изучили ранее. Подходя к освоению предмета подобным образом, студент рискует получить лишь поверхностные знания.
Цели и задачи: поддержать заинтересованность в предмете; поставить и решить задачу, требующую углубленных математических знаний.
Решение:
Студентке было предложено исследование на тему «Разреженные технологии в теории графов».
Для начала была поставлена задача отыскать в графе число маршрутов данной длины. В процессе решения использовать разреженные технологии [5].
Вывод:
В рамках данного исследования студентка более углубленно изучила некоторые темы из алгебры, численных методов, дискретной математики. Кроме того, она научилась читать не только учебную математическую литературу, но и статьи в научных журналах, и научные монографии [6].
Пример 5
Студентка ускоренного обучения направления подготовки «Информационные системы и технологии» подрабатывала в одной кофейне нашего города. Конечно, такие студенты редко бывают мотивированы на изучение не только математики, но и других предметов.
Цели и задачи:
– не дать потерять интерес к обучению в целом;
– помочь понять связь математических дисциплин с окружающим миром.
Решение:
Студентке была предложена научная работа, в которой надо было построить математическую модель работы кофейни, как системы массового обслуживания [7].
В кофейне принимаются заказы по двум кассам. Среднее количество заказов, поступающих в час – 80 чел. Среднее время оформления заказа – 1 мин. Определить показатели системы массового обслуживания.
Здесь n = 2, λ = 80 в час, t = 1 мин.
1. Интенсивность нагрузки.
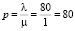
2. Время обслуживания (час).
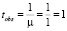
3. Вероятность, что канал свободен (доля времени простоя каналов).
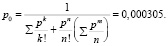
В ходе исследования были сделаны выводы, что кофейня перегружена и необходимо либо нанимать еще сотрудников, либо строить ещё одну кофейню по соседству.
Вывод:
При выполнении данной работы студентка убедилась в том, что полученные знания можно применить на практике даже там, где это, казалось бы, не представляется возможным [8].
Выводы
В описанных выше примерах поставленные в начале статьи задачи были решены. Студенты проявляли живой интерес к своей работе и предметам математического цикла в целом.
Конечно, многие из данных проектов с большой натяжкой можно отнести к серьезным научным исследованиям. Но сознание у студента, что он выполняет научную работу по интересующей его проблеме, повышает мотивацию к дальнейшему изучению математики.

