В настоящий момент одной из основных тенденций развития общества становится осознание того, что его развитие тесно связано с образованностью людей. Подготовка личности, отвечающей всем критериям – инициативного, деятельного специалиста, способного постоянно совершенствоваться, – сегодня имеет критическую важность.
Стремительное, постоянное обновление знаний, появление новых видов техники приводит к необходимости и преподавателям постоянно учиться и повышать квалификацию. Активное внедрение электронных технологий служит средством решения этих задач. Современные компьютерные средства способствуют повышению качества и скорости обучения, воспитанию информационной грамотности студента, пониманию необходимости продолжать самообучение в течение всей жизни.
Информационные технологии применяются при решении задач самых разных областей. Конечно, ни один компьютер не может заменить знания и опыт, которыми должны обладать молодые специалисты, но использование компьютера может помочь работать с большей отдачей и увеличить творческий потенциал специалиста.
Цель исследования: обзор преимуществ компьютерной визуализации при работе c поверхностями в курсе дифференциальной геометрии.
Материалы и методы исследования: анализ педагогической, психологической, методической и математической литературы.
Обучение – одно из средств познания окружающего мира, которое осуществляется с помощью органов чувств. Поначалу обучение было связано с трудовой деятельностью, что не вызывало каких-либо затруднений у детей, так как основой обучения были выполняемые операции. В дальнейшем обучение стало включать некоторые теоретические законы, которые невозможно было продемонстрировать вследствие их абстрактности. Появившееся противоречие между отвлеченностью передаваемых знаний и потребностью в создании чувственной опоры разрешил великий чешский педагог Ян Амос Коменский, который полагал, что познавать предметы необходимо на основе эмпирического восприятия. По его мнению, принцип наглядности составлял «золотое правило» дидактики. Крупнейший педагог-гуманист Иоганн Генрих Песталоцци, разработавший теорию природосообразного обучения, показал важность применения наглядности для формирования абстрактных понятий. Выдающийся российский ученый-педагог Константин Дмитриевич Ушинский подчеркивал, что главное в обучении – не обеспечение наглядности знания, а последующее формирование чувственного образа. Дальнейшее развитие педагогики подтвердило, что наглядность является важным и необходимым средством организации образовательного процесса на любом уровне [1].
Согласно исследованиям психологов, до 80 % информации человек получает через зрение [2], потому прием визуализации, будучи интересным и увлекательным для обучающихся, способен также стать сильнодействующим средством обучения. Это и делает актуальным исследование визуальных средств обучения [3].
На сегодняшний день наукой подтверждено, что пропускная способность органов чувств человека различна. Органы слуха пропускают в мозг больше информации, чем тактильные органы; органы зрения – больше, чем слуховые органы; то есть около 80 % всех сведений об окружающем мире человек получает с помощью зрения. Исследования показывают, что сопровождение словесной информации иллюстрацией значительно повышает уровень усвоения – до 65 % эффективности восприятия [4].
Жизнь человека протекает в мире образов – это обусловлено современной культурой и развитием цивилизации, – и потому естественно, что и обучение все больше визуализируется. Как методический прием, визуализация информации представлена еще в XVII в. в утопии Т.Кампанеллы «Город солнца» – «…во всем городе стены, внутренние и внешние, нижние и верхние, расписаны превосходнейшею живописью, в удивительно стройной последовательности отображающей все науки…». Описанный таким образом способ обучения можно считать наиболее правильным, идеальным образом получения образования [5].
Как сказал однажды К. Гаусс: «Математика – наука не столько для ушей, сколько для глаз». Наглядность и визуальные образы играют значительную роль в математике – недаром ещё древние математики пытались представлять самые элементарные алгебраические тождества в геометрическом виде. Без наглядных образов знания становятся бессодержательными и формальными, потому было немало сторонников разумной визуализации математики, среди которых и такие великие ученые, как Леонард Эйлер и Бернхард Риман [6].
Считается, что наглядное обучение обеспечивает разностороннее и полное формирование математических знаний и приводит к более высокому уровню развития математического мышления. В последние годы, в связи с переходом к информационному обществу, подспорьем для визуализации математического знания становятся компьютерные технологии [7]. И хотя мнения исследователей о компьютеризации геометрии расходятся, использование компьютера как инструмента оказывается крайне полезным в геометрических исследованиях, изучении многих вопросов и экспериментальном открытии новых фактов [8]. Весь спектр аспектов развития личности человека (его интеллект, эмоции, творческое мышление и др.) определяет потенциал использования информационных технологий в системе образования, в общем.
Эмоции являются неотъемлемой частью познания как процесса. Более того, успешная познавательная деятельность невозможна без эмоциональной составляющей – «большого напряжения и великой страсти требует наука от человека», как сказал академик И.П. Павлов [9]. Поэтому так важно, чтобы учителя и преподаватели воздействовали не только на когнитивную, но и на эмоционально-чувственную сторону воспитанников.
Общеизвестно положение, что процесс обучения и воспитания протекает успешнее, если педагог делает его эмоциональным. Где сегодня эта проблема активизации эмоций не стоит острее, как не в сфере обучения математике? Большинство учащихся убеждены, что математика слишком абстрактна и далека от их личных нужд, чтобы даже просто браться за чтение учебника или решение задач. И в таких условиях первостепенной задачей педагога является не «научить методам и приемам решения задач», как многие убеждены; но открыть ученикам элегантность, стройность и гармонию математики. Это возможно, если вызвать у студента интерес, мотивировать его.
Мотивация – один из важнейших психологических феноменов, который обеспечивает успех деятельности. В частности, высокомотивированные студенты учатся старательнее и достигают лучших результатов [10]. Мотивировать и развивать познавательный интерес у учащихся – важная и необходимая часть процесса обучения, и для этого нужно пользоваться всеми доступными средствами. Одним из таких средств является наглядность. Психологами установлено, что наглядность необходима в учебном процессе, так как выполняет важные функции – оживляет обучение, мотивирует и «настраивает» на процесс, добавляет убедительности абстрактным понятиям, способствует появлению у учащихся эмоционального отношения к изучаемому предмету. Использование различных функций наглядности способствует более плодотворному мышлению учащихся.
Реализация принципа наглядности при обучении математике является важным компонентом ввиду того, что все математические понятия – абстрактны, вследствие чего существует вероятность, что учащиеся будут воспринимать математику лишь как игру с символами, не осознавая связи изучаемых понятий с окружающим миром. Для получения знаний о свойствах математических объектов и о глубинных связях между ними и применяется наглядность.
Особенности мышления непосредственно влияют на формирование и развитие индивидуальности обучающегося. Логическое (аналитическое) мышление традиционно считается основным средством и целью процесса обучения. Но обилие достижений науки и техники XXI в. требует от человека создания чего-то исключительного и абсолютно нового. Логическое мышление связано с другими мыслительными операциями и не может считаться эффективным для создания нового продукта. Поэтому сегодня большее внимание уделяется развитию у учащихся других видов мышления, в частности, творческого.
Вообще говоря, разделение мышления на воспроизводящее (репродуктивное) и творческое (продуктивное) довольно условно, так как в любом мыслительном акте присутствует как творческая, так и исполнительная, проверяющая и реализующая, части. Процесс мыслительной деятельности или ее результат можно назвать творческим, только если он не мог быть получен после логического или алгоритмического вывода. Подлинно творческое деяние требует разрыва устоявшегося, логически обоснованного образа мыслей, возможного за счет иррационального начала.
Априори считается, что знание эффективно только при условии, что им пользуются творчески. Каждый человек изначально обладает творческими способностями, которые развиваются лишь при соответствующих условиях обучения и воспитания [11]. В формировании творческого мышления математике отведена значительная роль. Развитое творческое мышление может не раз помочь специалисту в решении многих задач будущей трудовой деятельности, в том числе тех задач, которые относятся к принятию ответственных решений. И хотя основной целью преподавания любого предмета является формирование специальных, предметных способностей, этими же средствами, и в том числе математическими, можно сформировать и развить гораздо больший набор способностей.
В связи со стремительной информатизацией сферы образования компьютерные технологии все чаще становятся подспорьем для визуализации математического знания. Несмотря на то, что в основном компьютерные технологии включаются в традиционный учебный процесс в качестве вспомогательных средств, в будущем, вне всякого сомнения, процесс обучения будет невозможен без современных информационных технологий. Так, с использованием компьютерных программ можно организовать различные формы учебно-познавательной деятельности студента, сделать целенаправленной и более активной самостоятельную работу обучающихся, углубить межпредметные связи, обеспечить личностно-ориентированный подход в обучении.
Если использование средств наглядности является важным элементом изучения математики, то изучение геометрии без них не представляется возможным. Но в ходе обучения этому предмету зачастую возникает проблема иного рода, а именно проблема развития пространственного воображения. После изучения планиметрии, когда все внимание было сосредоточено на двумерных объектах, учащимся непросто работать с пространственными телами. Поступая затем в высшее учебное заведение, бывший школьник сталкивается с еще более сложными задачами. В этих условиях очевидно, что необходимо обеспечивать студента такими технологиями обучения, которые отводили бы особое место наглядности знания.
В высшей школе большое внимание уделяется геометрическим курсам, где очень часто можно применять компьютерную графику для более полного визуального восприятия изучаемого материала. В курсе аналитической геометрии, к примеру, визуализация может помочь при изучении геометрических свойств таких объектов, как эллипс, парабола и другие кривые; эллипсоид, однополостный и двуполостный гиперболоиды и другие поверхности. При изучении поверхностей цилиндра и конуса демонстрируются динамические процессы сечения их плоскостями – для объяснения возможности изучения кривых второго порядка на основе конических сечений.
Возможности современных программных средств могут быть в особенности полезны при изучении теории поверхностей в рамках курса дифференциальной геометрии. Далеко не каждый человек может построить в своем воображении объемную фигуру по заданным уравнениям или условиям. Ранее учёные вынуждены были изображать исследуемые поверхности и тела самостоятельно – но такого рода упражнения будут непосильны для большинства студентов. Применение компьютерных средств визуализации в таких обстоятельствах становится важным и необходимым элементом обучения теории поверхностей.
Результаты исследования и их обсуждение
Не рассматривая в этой работе традиционные для дифференциальной геометрии кривые и поверхности (такие как астроида, циклоида и др.; тор, геликоид и др.), остановимся на тех поверхностях, которые, ввиду сложности описывающих уравнений, не включены в стандартный курс. Подобные функции сложно представить и изобразить самостоятельно. В этой связи неоценима роль компьютерных технологий. Их возможности позволяют не только без труда строить любые поверхности, но и давать волю фантазии, видоизменяя уже известные поверхности или даже придумывая новые.
К примеру, поверхность, полученная из катушки Миндинга (назовем ее спиралевидной катушкой), заменой функции для z и подбором диапазонов для u и v (рис. 1):
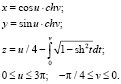

Рис. 1. Спиралевидная катушка
Так называемая (трижды) обмотанная катушкообразная поверхность (рис. 2) [12]:
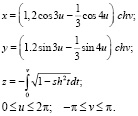

Рис. 2. Обмотанная торообразная поверхность
Следующие поверхности были построены именно вследствие творческого вдохновения, как ответ на вопрос: «Как будут выглядеть поверхности вращения с гипоциклоидами в качестве меридиан?» (рис. 3). Уравнения поверхностей и процесс их построения представлены в работе [13].


Рис. 3. Примеры поверхностей вращения с гипоциклоидными меридианами
Нельзя утверждать, что для воспитания личностных качеств и навыков, активизации творческого мышления или повышения качества усваиваемого учебного материала студентами достаточно только показывать им подобные иллюстрации. Учеба и мышление – это всегда деятельность самих студентов. При работе над поверхностями студенту полезными будут задания, которые не концентрируются исключительно на расчетах тех или иных характеристик поверхности. Возможности компьютерных технологий позволяют даже не самым успевающим ученикам без труда производить манипуляции над уравнениями и графическими образами поверхностей, руководствуясь только собственными фантазией и интуицией. Как показывает наш исследовательский опыт, подобная практика положительно сказывается как на понимании предмета, так и на формировании положительного к нему отношения.
Заключение
За последние годы было создано колоссальное количество новых технологий, которые фактически сделали компьютер мощным средством образования. Современный компьютер уже не просто средство для решения задач – расчетных, экономических, технических и т.д., – но и крайне важный элемент процесса формирования навыков, необходимых специалисту в его профессиональной деятельности.
На сегодняшний день преподавание без применения компьютерных технологий уже не представляется возможным, а овладение информационными технологиями является важным требованием к специалисту. Неоценимы преимущества программных средств в создании визуальных образов для трудно представимых объектов, таких как поверхности, заданные сложными параметрическими уравнениями. Вместе с тем использование компьютерной визуализации требует соответствующей подготовки учащихся в высших учебных заведениях. Высокий уровень подготовки специалистов является главным критерием эффективности работы учебного заведения.

