Студенты 1-го курса бакалавриата архитектуры с первого семестра занимаются архитектурным проектированием. Следовательно, с первых шагов обучения им предстоит овладевать методикой проектирования. Выясним толкование слова «проектировать» в разных словарях. У Ожегова [1] – это «намечать», по тезаурусу – «планировать», «составлять план», у Ушакова и Ефремовой [2, 3], – «собираться что-либо делать», «намечать осуществление чего-либо». Судя по словарному толкованию, овладевать методикой проектирования можно на любой дисциплине. И в первую очередь при изучении начертательной геометрии.
Цель исследования: изучение методики выбора наиболее оптимального варианта решения поставленной проблемы.
Объект исследования: задача по начертательной геометрии.
Метод исследования: сравнительный анализ решения задачи разными способами.
Сформулируем проблему: представить оптимальный вариант решения предложенной задачи.
Задача: построить линию пересечения конуса с плоскостью.
Намечаем этапы работы над проблемой.
- Задать условие.
- Изучить имеющиеся приёмы решения задачи.
- Провести сравнительную оценку этих приёмов.
- Проанализировать и оценить возможность применения этих приёмов в изменившихся условиях.
- Выбрать наиболее оптимальный вариант.
Задаём условие задачи. Возьмём вариант, когда ни одной проекции искомой линии пересечения заранее не задано. Пусть имеем наклонный конус, плоскость основания которого параллельна горизонтальной плоскости проекций. Секущая плоскость общего положения.
Изучая литературу, нашли 4 способа решения поставленной задачи.
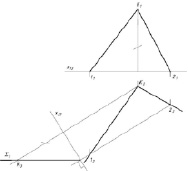
Метод вспомогательных секущих плоскостей [4].
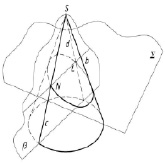
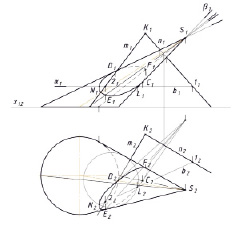
Проводим вспомогательную секущую плоскость β (проецирующую) так, чтобы она пересекала конус по простейшей линии. Поскольку основание конуса на горизонтальную плоскость проецируется в виде окружности, то вспомогательную плоскость можно выбрать параллельно основанию конуса. Ещё более простой вариант, когда вспомогательная плоскость проходит через вершину конуса (рис. 1, а). Cтроим линии пересечения вспомогательной плоскости с конусом (образующие с и d) и с заданной секущей плоскостью (прямая b). Отмечаем точки пересечения построенных линий: N = c ∩ b; L = d ∩ b. Эти точки будут принадлежать искомой линии пересечения плоскости ∑ с конусом. Затем строим ещё несколько точек и последовательно соединяем их с учётом видимости. На рис. 1, б, использованы и горизонтальная (α) и фронтально проецирующие вспомогательные плоскости (β).
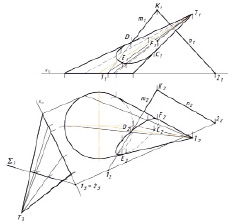
Гомологичное соответствие [5] (рис. 2).
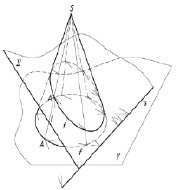
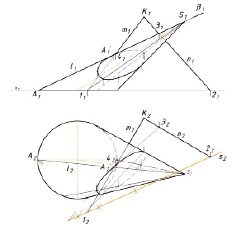
Из рис. 2, а, видно, что фигуры f' сечения и f основания конуса гомологично соответственные. Центром гомологии является вершина S, осью гомологии – линия s пересечения заданной плоскости Σ с плоскостью γ основания конуса: s = Σ ∩ γ. Точки A’ пересечения образующей l конуса с плоскостью Σ и А, через которую проходит эта образующая, будут гомологично соответственными. В ортогональных проекциях гомологичное соответствие возникает в поле π2 (рис. 2, б), где центр гомологии – проекция S2 вершины конуса. Ось гомологии s2 пройдёт через горизонтальные проекции 12 и 22 точек пересечения прямых m и n секущей плоскости Σ с плоскостью γ. Пара соответственных точек A2 > A2'. Остальные точки фигуры сечения определены гомологичными построениями. На фронтальную проекцию точки перенесены через образующие.
а) б)
Рис. 1. Метод вспомогательных секущих плоскостей: а) пространственный рисунок; б) эпюр
а) б)
Рис. 2. Гомологичное соответствие: а) пространственный рисунок: б) эпюр
а) б)
Рис. 3. Метод замены плоскостей проекций: а) преобразование секущей плоскости; б) решение задачи на эпюре
Замена плоскостей проекций [4, 6].
Преобразуем эпюр так, чтобы плоскость Σ общего положения стала проецирующей (рис. 3, а). В плоскости Σ проводим горизонталь 1–2 и задаём плоскость π3 ⊥ π2 и перпендикулярно горизонтали 1–2. На эпюре появится ось х23 ⊥ 1222 (рис. 3, а). Поскольку в π1 основание конуса расположено на х12, то в поле π3 оно будет находиться на оси х23 (рис. 3, б). В поле π3 плоскость Σ станет проецирующей. Искомое сечение совпадёт со следом Σ3 плоскости. Это будет та его часть, которая расположена в пределах изображения конуса. Через образующие конуса переносим точки искомого сечения сначала в поле π2, затем в π1 (рис. 3, б).
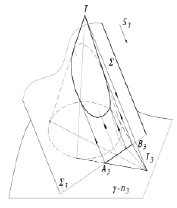
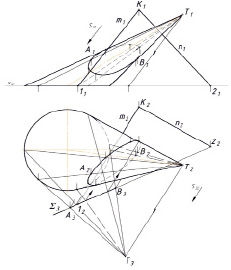
Дополнительное параллельное проецирование [7].
Сделать плоскость общего положения проецирующей можно и дополнительным параллельным проецированием, выбрав центр S3 в направлении, параллельном какой-либо прямой линии, лежащей в плоскости Σ. Дополнительную плоскость π3 совместим с плоскостью γ основания конуса. Построим дополнительную проекцию Т3 вершины конуса. Проекции основания конуса на π2 и π3 совпадут. Дополнительную проекцию конуса получим, проведя из Т3 касательные к основанию конуса (рис. 4, а). Проекция плоскости Σ на π3 представляет собой линию пересечения плоскостей Σ и γ и вырождается в след Σ3. Дополнительная проекция искомого сечения на π3 изображается отрезком А3В3 следа Σ3. В ортогональных проекциях решение показано на рис. 4, б. Через образующие конуса переносим точки сечения сначала в поле π2, затем в π1.
Во всех четырёх случаях эллипс построен по 6 точкам, 4 из которых расположены на очерковых образующих конуса. Как видно из рис. 1-4, результат получили один и тот же. Количество выполненных графических операций при решении задачи во всех четырёх случаях примерно одинаково. Оно колеблется от 22 до 24. Временные затраты приведены в первом столбце таблицы. Менее затратным при выбранном условии задачи оказался метод вспомогательных секущих плоскостей, наиболее трудоёмким – метод замены плоскостей проекций.
Изменим условие задачи. Пусть основание конуса находится во фронтально проецирующей плоскости, расположенной под углом к горизонтальной плоскости проекций (рис. 5, а). Снова решаем задачу рассмотренными выше четырьмя способами. Во всех четырех случаях она оказалась решаемой. Один из вариантов решения (гомологичное соответствие) представлен на рис. 5, а. Для построения оси гомологии пришлось воспользоваться дополнительной прямой d(d1, d2), лежащей в заданной секущей плоскости Σ. Ось s2 пройдёт через горизонтальные проекции 12 и 22 точек пересечения прямых m и d с плоскостью γ.⊥ π1. Пара соответственных точек A2 → A2' определена при помощи фронтально проецирующей плоскости β, проведённой через образующую l конуса. Временные затраты (таблица, столбик 2) увеличились из-за того, что при изменившемся положении плоскости основания конуса пришлось использовать дополнительные прямые линии заданной секущей плоскости. А при замене плоскостей проекций основание конуса в дополнительном поле проецируется в виде эллипса. Время ещё затрачено на построение его точек.
а) б)
Рис. 4. Метод дополнительного параллельного проецирования: а) пространственный рисунок; б) эпюр
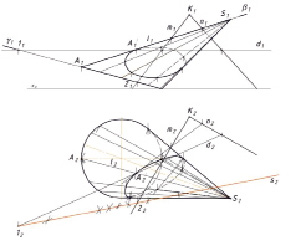
а)
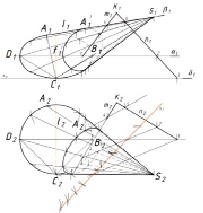
б)
Рис. 5. Изменённое условие задачи: а) основание конуса расположено во фронтально проецирующей плоскости; б) основание конуса в плоскости общего положения
Затраты времени на решение задачи
|
Расположение плоскости основания конуса |
Горизонтальная |
Фронтально- проецирующая |
Общего положения |
Средние затраты времени |
|
Метод |
||||
|
Вспомогательной секущей плоскости |
13 мин |
18 мин |
21 мин |
17,6 |
|
Гомология |
14 мин |
17 мин |
21 мин |
17,6 |
|
Замена плоскостей проекций |
19 мин |
22 мин |
28 мин |
23,0 |
|
Дополнительное параллельное проецирование |
16 мин |
20 мин |
– |
– |
Наконец возьмём общий вариант. Основание конуса лежит в плоскости общего положения (рис. 5, б) и опять решаем задачу четырьмя способами. Для удобства выполнения построений в основании конуса выделим треугольник DВС. В этом случае совершенно неприемлемым оказался 4-ый вариант. Очень трудно было подобрать направление дополнительного проецирования так, чтобы построение не выходило за пределы чертежа. Ситуация осложнялась ещё тем, что каждый раз необходимо строить точку пересечения прямой линии общего положения с плоскостью общего положения основания конуса. Остальные три варианта оказались снова решаемы. Результат в гомологичном варианте представлен на рис. 5, б. В этом случае гомологичное соответствие возникает между f1 и f1' в плоскости π1 и между f2 и f2' в плоскости π2. На рис. 5, б, гомологичные построения выполнены в плоскости π2. Ось гомологии s2, как горизонтальная проекция линии пересечения двух плоскостей Σ и γ общего положения построена при помощи вспомогательных плоскостей α и δ. Пара соответственных точек A2 → A2' определена путём построения точки пересечения образующей l с секущей плоскостью Σ. В плоскость π1 точки фигуры сечения перенесены через образующие конуса. Можно было сделать наоборот. Гомологичные построения выполнить в π1, а в плоскость π2 перенести через образующие. Не исключены и гомологичные построения в обеих плоскостях проекций. С плоскостью общего положения увеличилось время решения задачи, что видно из третьего столбца таблицы. Самым трудоёмким оказался метод замены плоскостей проекций.
Выводы
Проанализировав возможные ситуации поставленной проблемы, можно сказать, что в общем случае (т.е. независимо от способа задания условия) для её решения из четырёх рассмотренных вариантов приемлемы только три: метод вспомогательных секущих плоскостей, гомология и замена плоскостей проекций. В последнем столбце таблицы приведено среднее время решения задачи каждым приемлемым методом независимо от способа задания условия задачи. Менее затратными по времени оказались первые два: метод вспомогательных секущих плоскостей и гомология. Но по наименьшей загруженности чертежа линиями построения предпочтение следует отдать гомологии.
Итак, оптимальным вариантом решения предложенной задачи является гомология.
Заключение
На примере решения конкретной задачи начертательной геометрии показано, как путём анализа ситуации и цепочки логических рассуждений, можно разрешить поставленную проблему. Сформулированная проблема может быть выдвинута на абсолютно любой дисциплине, так как методика проектирования и ее способы аналогичны. Главными этапами в проектировании являются: анализ поставленной задачи, исследование предполагаемых решений и выбор наиболее оптимального варианта. Рассмотренные этапы подходят для решения задач всех видов проектирования. Полученные умения учитывать различные факторы решения поставленной проблемы и их анализ применимы в течении всего учебного процесса. Поэтому освоение методики проектирования крайне необходимо для продуктивной работы студента.

