На современном этапе Казахстан находится в состоянии непрерывной модернизации и реформирования системы образования в соответствии с современными требованиями развития казахстанского общества и условиями интеграции в мировое образовательное пространство.
В Послании Главы государства Касым-Жомарта Токаева народу Казахстана «Конструктивный общественный диалог – основа стабильности и процветания Казахстана» большое внимание уделяется вопросам повышения качества образования [1]. В Государственном общеобязательном стандарте начального образования подчеркивается необходимость создания условий для всестороннего развития обучающихся, способных найти свое достойное место в обществе [2]. Начальное образование является важным этапом основного среднего образования, так как на данном уровне формируется первоначальная система знаний, умений и навыков, необходимая для дальнейшего обучения. Каждый учебный предмет в начальной школе играет важную роль в формировании познавательной активности, развитии умений применять полученные знания для решения задач прикладного характера, готовности к жизни в современном информационном обществе. Учебный предмет «Математика» направлен на формирование у обучающихся первоначальных математических знаний для описания разнообразных объектов и явлений окружающей действительности, усвоение устных и письменных вычислительных алгоритмов, развитие общих приемов решения задач, умение выстраивать логические суждения на основе измерительных и вычислительных навыков [3]. Исходя из этого, можно сделать вывод о том, что в современном информационном мире математике отводится важная роль в развитии и становлении активной, самостоятельной личности.
В начальной школе геометрия не выделяется в отдельный предмет, но раздел «Элементы геометрии» включен в базовое содержание учебного предмета «Математика» и имеет существенное значение в развитии обучающихся [4]. Данный раздел включает три подраздела, которые представлены на рис. 1.
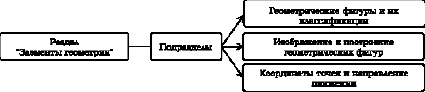
Рис. 1. Раздел «Элементы геометрии» и его подразделы
При изучении подраздела «Геометрические фигуры и их классификация» у обучающихся начальной школы формируются знания о геометрических фигурах, признаках и их видах – плоские (треугольник, круг, квадрат, прямоугольник, симметричные и несимметричные) и пространственные (куб, шар, конус, цилиндр, пирамида); умения измерять и строить геометрические фигуры с помощью измерительных и чертежных инструментов; сравнивать значения величин и преобразовывать единицы измерения; составлять и применять формулы нахождения периметра и площади прямоугольника, квадрата, треугольника и комбинированных фигур [5]. Младшие школьники, усваивая подраздел «Изображение и построение геометрических фигур», создают модели плоских фигур и составляют из их частей композиции, изготавливают развертки пространственных фигур, собирают их модель и др. Подраздел «Координаты точек и направление движения» направлен на реализацию цели определять расположение точек на числовом луче, на линии точек, на плоской фигуре точек относительно друг друга, составлять схемы движения объектов и др. Изложенное выше показывает, что с переходом на обновленное содержание образование происходит более углубленное изучение элементов геометрии, а также развитие пространственных представлений у обучающихся.
Результаты исследования и их обсуждение
Рассмотрим работу по усвоению элементов геометрии, проводимую на уроках математики в третьем классе. Обучающиеся знакомятся с окружностью, кругом и их элементами (центр, радиус, диаметр), симметричными и несимметричными фигурами, параллельными и пересекающимися прямыми, изучают площадь и ее единицы измерения, формулы нахождения площади прямоугольника, квадрата, прямоугольного треугольника и периметра комбинированных фигур, изготавливают развертку пространственных фигур и их модели, учатся определять расположения точек на плоской фигуре относительно друг друга, чертят фигуры и определяют ее координаты. Следует подчеркнуть, что они проявляют огромный интерес при изучении элементов геометрии, легко запоминают названия геометрических фигур и выделяют их существенные и несущественные свойства в процессе практических действий с ними.
Практическая часть в третьем классе основывается на составлении композиций из моделей фигур, конструировании и моделировании из палочек, пластилина, проволоки, что позволяет закрепить устойчивый образ фигуры в памяти младшего школьника. Для обобщения полученных ранее знаний в 1–2 классах о плоских и пространственных геометрических фигурах, их существенных признаков и особенностей, используем метод «Заполни пробелы». Целью данного метода является упорядочение и восстановление в памяти младших школьников общих свойств геометрических фигур. Каждому обучающемуся раздается карточка с заданием и за определенный промежуток времени необходимо вспомнить изученный ранее учебный материал и заполнить пропуски:
- Геометрические фигуры делятся на две группы _________.
- Закрась плоские фигуры и обведи в круг пространственные фигуры.

- Перечисли пространственные фигуры ____________.
- Прямоугольник – это четырехугольник, у которого _______.
- Фигура, у которой все стороны равны, все углы прямые, называется _________.
- Геометрическая фигура, которая имеет три стороны и три угла_______
- Фигура на плоскости, у которой нет углов? _________ .
Таким образом, обучающиеся выходят на тему урока «Окружность, круг и их элементы». Важным моментом при формировании данных понятий является выяснение, что им уже известно о данных фигурах, какие различия они могут назвать и где фигуры встречались им в повседневной жизни. Поэтому одной из главных задач при формировании у младшего школьника умения узнавать форму разных предметов в соответствии с определенными геометрическими фигурами является умение абстрагировать форму от вещи и видеть ее в других предметах и, проводя интеллектуальную переработку, выделять в нем наиболее существенные признаки.
Обучающиеся, используя различные источники информации, формулируют более полные и точные определения понятий «круг» и «окружность», обобщая, конкретизируя полученную информацию. Чтобы младшие школьники правильно усвоили данные понятия, им необходимо создать модель окружности и круга, с этой целью применяется проволока или бельевая веревка для изготовления модели окружности, а модель круга создается из картона так, чтобы она помещалась в окружность. Важно, чтобы они осознали то, что окружность ограничивает круг и является его границей. Для закрепления данных понятий и применения их в дальнейшем предлагается метод «Классификация», в котором необходимо распределить по двум столбикам перечень предметов, в первый записать предметы, которые имеют форму круга, а во второй – окружности (крышка, бублик, тарелка, кольцо, блин, зеркало, браслет). Критерием оценивания является умение определять обучающимся фигуру предмета: круг или окружность. Данный метод способствует развитию умения выделять существенные признаки данных понятий и устанавливать между ними сходство и различие.
Младшим школьникам можно предложить провести исследовательскую работу «Пицца», используя вырезанный круг из бумаги и выполняя действия согласно инструктажу учителя:
1. Согни пиццу ровно пополам 2 раза.
2. Разверни пиццу, найди точку пересечения двух линий. Это центр пиццы. Обозначь буквой «О». Сколько половин в круге? Какие получились части? (одинаковые, они совмещаются, если приложить одну часть к другой). Какая линия сгиба? (прямая). Есть ли у нее начало и конец? Это отрезок.
3. Линия сгиба – это диаметр. Он делит пиццу пополам. Обозначь его буквой D и обведи синим цветом. Сколько диаметров можно провести?
4. Линия, соединяющая край пиццы и ее центр, называется радиус и обозначается буквой R. Обведи его зеленым. Сколько радиусов можно провести? Что вы можете сказать про размеры радиуса и диаметра? Диаметр равен двум радиусам.
Так, сгибая лист бумаги, выделяя все это цветными карандашами, обучающиеся наглядно знакомятся с элементами круга и окружности, что позволяет научиться чертить, а также определять центр, радиус и диаметр окружности. Таким образом, выполняя действия согласно алгоритму и слушая комментарии учителя, знакомятся с данными понятиями. После того как обучающиеся выполнили исследовательскою работу, с помощью приема «Верные и неверные утверждения» проводится анализ усвоенного материала.
|
Верные и неверные утверждения |
+ / – |
|
Окружность – это замкнутая линия |
+ |
|
Расстояние от центра до любой точки окружности всегда одинаково |
+ |
|
В окружности можно провести только один диаметр |
– |
|
Радиус окружности равен двум диаметрам |
– |
|
Диаметр – отрезок, который соединяет две точки окружности и не проходит через центр окружности |
– |
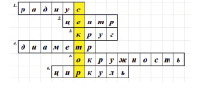
Для закрепления данных понятий обучающиеся разгадывают кроссворд (рис. 2).
|
|
|
Рис. 2. Кроссворд
Практические действия с геометрическим фигурами играют значительную роль в успешном овладении данными понятиями и их существенными признаками. Для этого используется метод моделирования, суть которого заключается в следующем: обучающимся предлагается создать модель круга и окружности с ее элементами из пластилина и прикрепить на картон. При изучении данного учебного материала необходимо также вспомнить пространственную геометрическую фигуру шар и провести параллель между понятиями. Младшим школьникам предлагается создать в группе мини-проект «Парад планет».
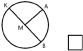
При изучении окружности и круга большое значение отводится правильному построению окружности. Для начала младшим школьникам предлагается обсудить в паре, как без чертежных инструментов нарисовать окружность и круг. Знакомство с чертежным инструментом циркулем происходит с рассмотрения строения данного устройства, а также с инструктажа педагога о технике безопасности при работе с циркулем. Далее выполняется построение окружности, при котором учитель все практические действия выполняет у доски и комментирует, обращая внимание на правильное построение, а обучающиеся в своих рабочих тетрадях. Выполнив построение, предлагаем закрасить полученную окружность синим цветом, а внутреннюю область окружности желтым цветом, тем самым обращая внимание на различие данных понятия. Особое внимание уделяется алгоритму построения окружности произвольного или заданного радиуса, обозначая буквами центр, радиус и диаметр окружности. При измерении радиуса и диаметра окружности обучающиеся делают вывод о том, что радиус окружности меньше, чем диаметр, в два раза. Для выработки навыка правильного построения окружности с помощью циркуля предлагаем младшим школьникам создать проект «Сказочное животное» (рис. 3).




Рис. 3. Проект «Сказочное животное»
В ходе выполнения практических задач на построение геометрических фигур важно научить младших школьников пользоваться различными чертежными инструментами, а также соблюдать алгоритм построения, являющийся необходимым средством развития мышления обучающихся. Первые построения целесообразно выполнять по образцу, далее обучающиеся самостоятельно чертят геометрические фигуры, следуя алгоритму. Немаловажное значение имеет развитие логического мышления у младших школьников при построении разнообразных предметов или их недостающих частей.
После того как младший школьник овладел умением чертить круг и окружность по заданному радиусу, можно предложить следующую практическую работу: нарисовать графические орнаменты или сюжетную картину с помощью циркуля.
Для закрепления изученной темы предлагаются задания на определение элементов окружности и на нахождение радиуса и диаметра окружности.
Задание 1. Отметь окружность. Дополни таблицу
|
|
|
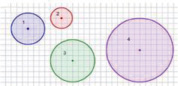
Задание 2. Найди длину диаметра и радиуса каждого круга. Обрати внимание на единицы измерения.
|
|
Круг 1: диаметр ____ см, радиус ____ см Круг 2: диаметр ____ мм, радиус ____ мм Круг 3: диаметр ____ см, радиус ____ см Круг 4: диаметр ____ см, радиус ____ см |
Знакомство с симметричными и несимметричными плоскими фигурами начинаем с приема «Лишнее слово», где обучающимся необходимо найти в таблице изученные плоские геометрические фигуры и термин «симметрия». Младший школьник, определяя признак, объединяющий группу данных слов, исключает лишнее слово и тем самым подходит к изучению новой темы. Целью данного приема является развитие логического мышления, навыков абстрагирования и обобщения, а также выделение существенных признаков предметов.
|
Д |
Ж |
Е |
П |
Л |
Д |
П |
К |
А |
Т |
К |
О |
Ч |
Д |
Ж |
Е |
П |
Л |
Д |
П |
К |
А |
Т |
К |
О |
Ч |
|
|
О |
В |
К |
В |
А |
Д |
Р |
А |
Т |
Ш |
Р |
Д |
Е |
О |
В |
К |
В |
А |
Д |
Р |
А |
Т |
Ш |
Р |
Д |
Е |
|
|
Х |
П |
А |
Д |
К |
О |
Я |
П |
Р |
Е |
У |
Г |
Т |
Х |
П |
А |
Д |
К |
О |
Я |
П |
Р |
Е |
У |
Г |
Т |
|
|
Ы |
Р |
О |
Т |
Р |
К |
М |
А |
Д |
С |
Г |
В |
Ы |
Ы |
Р |
О |
Т |
Р |
К |
М |
А |
Д |
С |
Г |
В |
Ы |
|
|
С |
И |
Щ |
Р |
А |
Р |
О |
З |
М |
Ф |
Й |
О |
Р |
С |
И |
Щ |
Р |
А |
Р |
О |
З |
М |
Ф |
Й |
О |
Р |
|
|
И |
У |
З |
Е |
К |
У |
У |
Г |
З |
О |
Г |
Ф |
Е |
И |
У |
З |
Е |
К |
У |
У |
Г |
З |
О |
Г |
Ф |
Е |
|
|
М |
К |
В |
Д |
Г |
Ш |
Г |
Е |
С |
К |
В |
Х |
Х |
М |
К |
В |
Д |
Г |
Ш |
Г |
Е |
С |
К |
В |
Х |
Х |
|
|
М |
Г |
М |
Г |
О |
Р |
О |
И |
А |
Р |
О |
Ы |
У |
М |
Г |
М |
Г |
О |
Р |
О |
И |
А |
Р |
О |
Ы |
У |
|
|
Е |
В |
Ц |
В |
У |
В |
Л |
Х |
Х |
У |
А |
Л |
Г |
Е |
В |
Ц |
В |
У |
В |
Л |
Х |
Х |
У |
А |
Л |
Г |
|
|
Т |
Д |
В |
А |
З |
О |
Ь |
Ц |
Ю |
Ж |
В |
Я |
О |
Т |
Д |
В |
А |
З |
О |
Ь |
Ц |
Ю |
Ж |
В |
Я |
О |
|
|
Р |
О |
И |
К |
Х |
У |
Н |
И |
Ч |
Н |
Д |
Ж |
Л |
Р |
О |
И |
К |
Х |
У |
Н |
И |
Ч |
Н |
Д |
Ж |
Л |
|
|
И |
У |
О |
Х |
В |
Ю |
И |
Ю |
М |
О |
Н |
Х |
Ь |
И |
У |
О |
Х |
В |
Ю |
И |
Ю |
М |
О |
Н |
Х |
Ь |
|
|
Я |
С |
Р |
Р |
А |
А |
К |
Ы |
Н |
С |
Ж |
Ц |
Н |
Я |
С |
Р |
Р |
А |
А |
К |
Ы |
Н |
С |
Ж |
Ц |
Н |
|
|
М |
А |
Е |
К |
О |
С |
Л |
Н |
К |
Т |
У |
И |
И |
М |
А |
Е |
К |
О |
С |
Л |
Н |
К |
Т |
У |
И |
И |
|
|
А |
Е |
Т |
Р |
Е |
У |
Г |
О |
Л |
Ь |
Н |
И |
К |
А |
Е |
Т |
Р |
Е |
У |
Г |
О |
Л |
Ь |
Н |
И |
К |



Рис. 4. Игра «Симметрия»
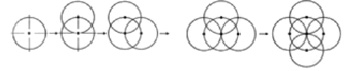
Изучение понятия «симметрия» целесообразно начать с практической работы. У каждого на парте лежат фигуры, сгибая и наблюдая за ними, обучающиеся, таким образом, знакомятся с понятиями «симметрия», «симметричные фигуры», «ось симметрии». Далее следует провести игру «Симметрия», заключающуюся в том, что младший школьник в силу своих возможностей выбирает круг, содержащий 2, 4, 8 секторов, из которых один заполнен определенным узором, к нему прилагается конверт с разнообразными геометрическими фигурами. Задача обучающегося составить симметричное отражение, используя фигуры, в соответствии с изображением первого сектора (рис. 4).
Данное задание формирует у младших школьников представление о симметрии, симметричных фигурах и о том, что фигуры могут содержать несколько осей симметрии, а также способствует развитию логики, образного мышления, мелкой моторики.
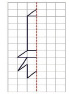
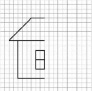
Практическая работа по построению симметричных плоских фигур проводится в виде графических диктантов, рисованию по клеткам. Младшим школьникам предлагается в группе исследовать и выявить симметрию цифр, букв, тела человека и его одежды, зданий.
Задание: Дорисуй фигуру, соблюдая принципы симметрии.
|
Уровень 1. |
Уровень 2. |
Уровень 3. |
|
|
|
|
Обучающиеся также выполняют творческие задания способом монотипия: на линии сгиба бумаги с помощью шаблона создают изображение половины бабочки, елки, лягушки или гриба, листа клена, покрывают данный рисунок краской и, накладывая другую половину бумаги, получают отпечаток целого изображения. После выполнения задания подводятся итоги изученной темы.
Урок по теме «Площадь. Единицы площади» имеет несколько этапов. На первом этапе младшие школьники сравнивают определенные предметы по площади, которые совершенно отличаются друг от друга или одинаковы, устанавливая при этом отношения «больше», «меньше», «равно», при этом используются различные способы измерения площади: на глаз или наложением предметов, а также разнообразные мерки. Например, младшим школьникам предлагается измерить поверхность парты, используя нестандартные мерки. В ходе обсуждения после выполненной практической работы составляется диаграмма, которая содержит разные результаты измерения. В процессе обсуждения приходим к выводу о необходимости использования стандартной мерки для измерения площади.
На втором этапе обучающиеся знакомятся с таким инструментом для измерения площади геометрических фигур, как палетка, применение которого способствует пониманию смысла измерения площади, а именно подсчет единичных квадратов, которые умещены в измеряемой фигуре. При этом необходимо, чтобы обучающиеся уяснили алгоритм вычисления площади при помощи палетки:
1. Наложить палетку на фигуру.
2. Сосчитать количество полных ква- дратов.
3. Сосчитать количество неполных квадратов и разделить полученное число на 2.
4. Найти приблизительную площадь данной фигуры, сложив число полных квадратов и неполных квадратов, деленное на 2.
Обучающиеся находят площадь геометрических фигур с использованием палетки, знакомятся с единицей измерения площади – квадратный сантиметр, квадратный дециметр и квадратный метр. В процессе изучения единиц измерения площади, их сравнения и нахождения значения выражений у некоторых обучающихся возникают трудности, что приводит к пассивности. Для того чтобы включить в активную деятельность весь класс, необходимо использовать опорные схемы «Единицы измерения площади». Младший школьник, опираясь на схемы, экономит время при изложении материала и приобретает больше уверенности при ответе и, таким образом, запоминает изучаемый материал, что способствует повышению успеваемости и обеспечивает успешную работу на уроке. Для закрепления единиц измерения площади предлагаются задания, где необходимо заполнить пропуски:
|
16м2 = _________ дм2 |
29дм2 = ________ см2 |
8м2 = __________ см2 |
3м2 = __________ см2 |
Площадь геометрической фигуры можно вычесть путем пересчета единичных квадратов (палетка, модель квадратного сантиметра) и косвенным путем (используя формулы). Таким образом, на следующем этапе младший школьник вычисляет площадь квадрата, прямоугольника и прямоугольного треугольника с применением формулы. Перед обучающимися ставится вопрос о том, как можно вычислить площадь фигуры быстрее, не подсчитывая количество единичных квадратов или используя палетку. В процессе этого вводятся формулы нахождения площади прямоугольника и квадрата. Данные формулы закрепляются в ходе решения задач.
В ходе изучения формул вычисления площади необходимо проиллюстрировать младшим школьникам прямую и обратную пропорциональную зависимость между величинами. У обучающихся нередко возникают ошибки в понятиях «площадь» и «периметр». Поэтому в процессе изучения формул нахождения площади фигур целесообразно повторить периметр и установить различия в данных понятиях, а также обратить внимание на разницу в названиях единиц измерения периметра и площади. Площадь – часть плоскости, которую занимает фигура, ограниченная замкнутой кривой или ломаной линией. Младшие школьники, выделяя разными цветами замкнутую линию и внутреннюю часть фигуры, проводят параллель между понятиями «площадь» и «периметр», при этом, опираясь на прежний опыт обучающихся, даем возможность самостоятельно делать выводы. Для закрепление формулы нахождения периметра и площади прямоугольника выполните задание, где нужно заполнить пропуски в таблице:
|
a |
8 см |
11 см |
||
|
b |
4 см |
6 дм |
20 см |
|
|
P |
40 см |
1 м |
||
|
S |
72 м2 |
В ходе выполнения заданий на вычисление площади и периметра прямоугольника необходимо показать, что геометрические фигуры, которые имеют одинаковую площадь, могут иметь разные периметры, и, наоборот, прямоугольники, имеющие одинаковый периметр, могут иметь неодинаковые площади. Обучающиеся чертят прямоугольники с заданными сторонами, вычисляют площадь и периметр, записывая их в таблицу. Полученные результаты позволяют младшим школьникам наглядно осознать соотношения между периметром и площадью.
Заключение
Исходя из вышеизложенного, следует сделать вывод о том, что на уроках математики необходимо вести систематическую работу по изучению элементов геометрии, являющейся важной составляющей образовательного процесса при обучении предмета «Математика». Применение учителем начальных классов наглядности, исследовательских и активных методов обучения, алгоритма при проведении практических работ, способствует развитию у обучающихся образного мышления и пространственного воображения, навыков анализа и синтеза, умений сравнивать и обобщать предметы по признаку, классифицировать геометрический материал, а в дальнейшем применять эти знания, умения и навыки на следующих уровнях образования при изучении предмета «Геометрия» и в процессе собственной жизнедеятельности.