Изучение классического закона всемирного тяготения в рамках школьной программы, как правило, ограничивается ознакомлением с математической записью этого закона [1–3],
,
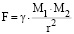и объяснением причины отсутствия столкновения космических тел их вращением (рис. 1) вокруг друг друга [4, с. 18], которое подчиняется формуле
.
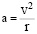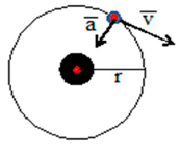
Рис. 1. Схема вращения космического тела вокруг источника гравитационного поля
Например, Луна вращается вокруг Земли, Земля вокруг Солнца, Солнце вокруг центра Галактики. Проблемы тёмной энергии и тёмной материи обычно подробно не обсуждают. Между тем возникают естественные вопросы: «А если мгновенно остановить вращение, например, Луны вокруг Земли, то через какое время они столкнутся и с какой скоростью? Какие расстояния преодолеют перед столкновением?» Авторы учебников избегают в своих книгах ответы на эти вопросы в силу кажущейся сложности выражений, необходимых для соответствующих расчётов.
Целью настоящей работы является проверка возможности обучения учащихся самостоятельно рассчитывать ответы на подобные вопросы, используя математику исключительно в объёме школьной программы [5–7].
Материалы и методы исследования
В качестве методов исследования применяли анализ процесса сближения двух масс под действием сил гравитации и комбинирование математических действий и операций, предусмотренных общеобразовательными стандартами [7].
Результаты исследования и их обсуждение
Считается, что вычисление скоростей столкновения двух масс под действием сил гравитации, расстояния, преодолеваемого ими при этом, а также времени сближения двух масс слишком сложно для учащихся общеобразовательных школ. На первый взгляд, действительно, точное время t столкновения должно вычисляться по формуле:
,
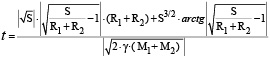где R1 и R2 – радиусы сталкивающихся масс M1 и M2 соответственно, S – первоначальное расстояние между их центрами, γ – гравитационная постоянная. Скорость столкновения требует следующих расчётов:
,
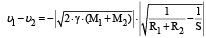где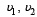 
– противоположно направленные скорости столкновения масс M1 и M2.
При этом подразумевается, что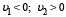 
и 
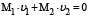, а расстояния S1 и S2, преодолеваемые массами M1 и M2 до столкновения, находятся из соотношения
.
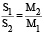Однако отметим, что все эти вычисления не требуют от учащихся знаний, превышающих школьную программу. Учащемуся необходимо лишь владеть умением извлекать квадратные корни, пользоваться дробными показателями степеней, составлять и решать системы двух уравнений с двумя неизвестными. Относительная громоздкость некоторых расчётов может потребовать также навыков использования современных калькуляторов. Рассмотрим конкретный пример.
Задача
При мгновенной остановке вращения Луны вокруг Земли эти два космических тела столкнутся под действием силы тяготения. Через какое время t это столкновение произойдёт? С какими скоростями ʋ1 и ʋ2 соответственно эти космические тела встретятся? Какой путь к Земле (S1) преодолеет до столкновения Луна и какой путь к Луне (S2) преодолеет Земля? Учесть, что расстояние S между центрами Луны и Земли 384 467 км, масса (M1) Луны 7,35∙1022 кг, масса (M2) Земли 6,0·1024 кг, радиус Луны (R1) 1378 км, средний радиус Земли (R2) 6371 км, гравитационная постоянная 6,67·10-11 Н·м2/кг2. При решении можно воспользоваться формулами
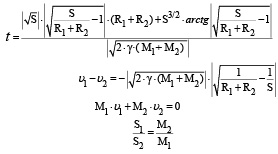
Большого объёма предложенной задачи легко избежать преподавателям и авторам учебных пособий, разбив её на три:
− задачу о нахождении времени столкновения;
− задачу на расчёт скоростей столкновения заданных масс;
− задачу на вычисление расстояний, преодолеваемых сталкивающимися массами.
Заметим, что эта же самая или аналогичная задача может быть поднята до уровня олимпиадной простым устранением из условия готовых формул. В этом случае участнику олимпиады придётся эти формулы выводить, что опять-таки не потребует от него знаний математики, превышающих школьную программу, однако понадобится более глубокое понимание математического аппарата дифференциального и интегрального исчислений. В частности, участник олимпиады должен продемонстрировать понимание соответствия физических величин математическим действиям, а именно: определять скорость как производную расстояния или интеграл ускорения, ускорение – как производную скорости, расстояние – интеграл скорости.
Рассмотрим один из вариантов вывода формул, приведённых в условии рассмотренной задачи.
Проведём ось ОХ через Землю и Луну, не вращающуюся вокруг планеты, обозначив х1 – положение Луны, х2 – положение Земли (рис. 2).
Рис. 2. Схема взаиморасположения Луны и Земли, сталкивающихся вследствие мгновенной остановки вращения спутника вокруг планеты
Обозначим также а1= х1″ – ускорение Луны, а2 = х2″ – ускорение Земли, М1 – масса Луны, М2 – масса Земли.
Из рисунка видно, что
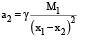
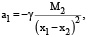
где γ – гравитационная постоянная.
Следовательно,
.
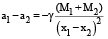Вводя обозначения
х1 – х2 = r;
γ·( М1 + М2) = K, (1)
сможем записать
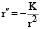. (2)
Если обозначить
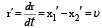, (3)
то из условия задачи вытекает, что
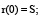
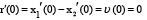(м/с).
Поскольку величина r зависит от времени t, то
.
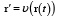То есть для того, чтобы выразить величину r″ из последнего равенства, необходимо взять производную сложной функции:
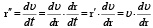. (4)
При t = 0
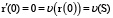
То есть ʋ(S) = 0, что вполне соответствует здравому смыслу.
Сопоставляя (2) и (4), можем записать
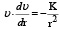
или (после разделения переменных)
.
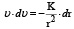Проинтегрируем полученное равенство до момента столкновения
,
,
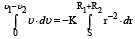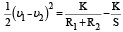Подставив вместо K его значение из (1), получим
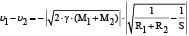.(5)
Для нахождения отдельно ʋ1 и ʋ2 необходимо ещё одно уравнение, включающее эти две величины. Выведем его, пользуясь равенством:
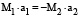
или
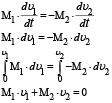
С учётом формулы (5) получаем систему двух уравнений с двумя неизвестными для расчёта ʋ1 и ʋ2.
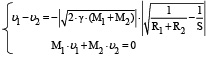
Для расчёта времени столкновения t воспользуемся обозначениями (1) и (3) и представим (5) в виде равенства, справедливого на протяжении всего движения Луны и Земли навстречу друг другу.
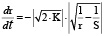
или
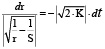
Проинтегрировав полученное равенство до момента столкновения t, при котором r = R1 + R2
,
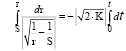получим
.
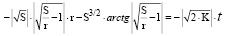Следовательно,
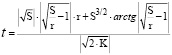
или
.
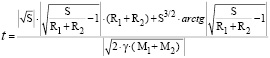Для нахождения расстояний, преодолеваемых Луной (S1) и Землей (S2) перед столкновением, исходим из неизменности положения центра масс в течение всего процесса сближения космических объектов. В данном случае положение этого центра определяется выражением
.
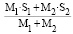Если в момент остановки вращения Луны за начало оси ОХ принять положение Земли, то
.
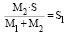Если в этот момент за начало оси принять положение Луны, то
.
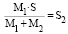Следовательно,
.
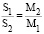Заключение
Задачи по расчёту:
− скоростей тел, сталкивающихся под действием сил гравитационного притяжения;
− времени, требующегося для их сближения;
− расстояния, преодолеваемого при этом телами, –
могут быть сформулированы для любой пары масс и предложены старшеклассникам на уроках физики или естествознания при условии указания основных формул, необходимых для решения, а также участникам школьных олимпиад по физике, которые должны будут выводить эти формулы самостоятельно.