Культура принятия решений, т.е. умение находить и обосновывать решения, востребована в любой интеллектуальной области. Это требует от человека творческого подхода к своей деятельности. Бесспорно, что навыкам творить, т.е. открывать неизведанное, наиболее продуктивно учит математика. Поэтому очевиден вывод: надо повышать математическую культуру школьников, чтобы решение творческих задач для них стало скорее нормой, чем исключением [1].
В настоящее время поступить в престижный технический вуз могут выпускники, которые зарекомендовали себя в олимпиадном движении и набрали высокий балл по ЕГЭ. Однако стандартная школьная программа по математике не способствует ни тому, ни другому. В результате школьники прибегают к услугам репетиторов, среди которых хороших мало. И, как правило, репетиторы не учат творчеству, а лишь натаскивают на стандартные приемы, зарекомендовавшие себя как ведущие к цели с минимальными затратами. Обычно репетиторы не выходят за рамки школьной программы, ставя перед школьником цель прилично сдать ЕГЭ. Однако если школьник хочет участвовать в олимпиадном движении, то репетиторы помогают мало. Тут нужен принципиально иной подход, способствующий развитию творческого потенциала школьника и формированию математической культуры.
Исходя из этих предпосылок, автор реализовал программный комплекс «Живая математика», отражая тем самым мысль, что математика не статична, а представляет собой развивающийся организм. Отметим, что «Живая математика» не решебник, содержащий большое число решений самых разных задач. Реализованный в продукте подход в корне иной – дать возможность ученику самостоятельно найти решение, используя подсказки в трудных местах и прибегая к тем приемам решений, которыми в изобилии располагает система. Достаточно подробно «Живая математика» представлена в [2], поэтому здесь на ее особенностях не останавливаемся. Следует лишь отметить, что в «Живой математике» автор реализовал концепцию единой среды математики, которой представляется школьная математика. Так, развитое геометрическое мышление помогает при решении алгебраических и тригонометрических задач, а свободное владение алгебраическими навыками позволяет увидеть в геометрических задачах аспекты, без этих навыков незаметные. Наконец, развитое комбинаторное мышление необходимо не только в школьной математике, так как позволяет формировать логический каркас рассуждений, приводящих к искомому решению.
Одним из компонентов «Живой математики» является подсистема «Алгебраист», представляющая собой среду решения алгебраических задач. В «Алгебраисте» собраны все преобразования, необходимые для решения задач школьной алгебры. Однако «Алгебраист» не является алгебраическим калькулятором, выполняющим элементарные алгебраические преобразования. Система представляет собой среду со своим языком описания алгебраических выражений, механизмом выбора преобразований, средством формирования протокола, позволяющего сохранить решение, и пр. Протокол избавляет пользователя от необходимости использовать дополнительный инструмент для сохранения промежуточных вычислений в базе данных. Потом, с целью дополнительного анализа, решение может быть использовано несколько раз. Тем самым «Алгебраист» реализует и функции решебника. Поэтому всегда можно вернуться к уже решенным задачам с целью разбора их решений. В заключение отметим, что «Алгебраист» реализован на языке Python, который, с одной стороны, содержит все необходимые средства, а с другой, обеспечивает вполне приемлемую эффективность программы [3].
В статье демонстрируются основные особенности системы «Алгебраист» с целью дать общее представление о ее возможностях при изучении школьного курса алгебры.
Назначение подсистемы «Алгебраист»
Умение преобразовывать алгебраические выражения дает существенное преимущество ученику при решении большого числа задач, связанных с преобразованием выражений. К ним относятся, например, задачи упрощения алгебраических выражений, решения уравнений и неравенств, тригонометрических преобразований и пр. Владея устойчивыми навыками алгебраических преобразований, школьник может легко свести исходное выражение к наиболее выгодному виду. Например, разложить на множители, чтобы потом найти решение уравнения, частное от деления многочленов и пр. Отметим, что вынесение, например, нетривиального множителя в алгебраическом или тригонометрическом выражении далеко не тривиальная задача. Поэтому «Алгебраист» учит ученика видеть, как преобразовывать алгебраическое выражение, предоставляя для этого все необходимые в школьном курсе алгебраические преобразования. Это позволяет ученику легко получить различные результаты по исходному выражению: приведение подобных, умножение и деление полиномов, вынесение общих множителей, разложение на множители, сокращение полиномов и т.п.
В случае алгебраических преобразований какого-то единого окончательного результата быть не может, так как последний определяется условием задачи. Поэтому, имея под рукой необходимые преобразования, ученик сможет получить результат, который, как ему кажется, быстрее приводит к решению. Исходя из этого, подсистема «Алгебраист» позиционируется как среда решения алгебраических задач со своим языком описания алгебраических выражений, интерпретатором преобразований, средством протоколирования и сохранения решений и т.п. В итоге ученику предоставляется возможность при поиске решения совершать разнообразные алгебраические преобразования, которые существенно перекрывают программу средней школы. Тем более что в средней школе часть материала по алгебре проходится поверхностно или вообще не проходится. Это определяется конкретным уровнем класса и снижением общей математической культуры школьников.
В системе «Алгебраист» используются приемы искусственного интеллекта, что определяется следующими причинами [4]. Не приходится говорить о наличии некоторого универсального алгоритма решения алгебраических задач. Например, задача разложения многочлена на множители обладает существенной неопределенностью, что может привести к разным результатам, причем одни могут привести к окончательному решению, другие – нет. От навыков получать эти результаты и легко с ними оперировать зависит успех в поиске искомого решения. Эта идея в полной мере реализована в «Алгебраисте», в котором подразумевается возможность использования различных вариантов поиска. Основные методы искусственного интеллекта, представленные в «Алгебраисте», суть разнообразные стратегии поиска, которые могут выбираться пользователем или самой системой, если подразумевается автоматическое решение. Описание этих стратегий приводится в более подробной инструкции по пользованию системой, чтобы понимать, какие из них лучше использовать в том или ином случае.
Язык описания алгебраических выражений и интерфейс подсистемы «Алгебраист»
Кратко опишем те параметры «Алгебраиста», с которыми приходится иметь дело пользователю. Ориентируясь на пользователей, которые не обладают глубокими знаниями в области ИТ, система «Алгебраист» характеризуется весьма простым интерфейсом и понятным языком описания алгебраических выражений. Последний практически ничем не отличается от обычного языка, за исключением того, что операция возведения в степень использует символ ^, а не запись показателя степени над строкой. Так, выражение x2 представляется в виде x^2, а одночлен 2y2z3 представляется в виде 2y^2z^3. Это обычная запись степенных выражений, используемая в языках программирования. В тех местах, где требуется знак умножения, используется звездочка *, так же как в языках программирования. Скобки используются только круглые и соглашения, касающиеся их, принимаются без изменения. К такому языку пользователь легко привыкает, и поэтому ввод исходных данных задачи при работе с «Алгебраистом» не вызывает затруднений.
Чтобы не загромождать изложение излишними деталями (кроме того, цель статьи состоит в предварительном знакомстве с «Алгебраистом»), здесь не приводятся снимки экрана для представления интерфейса. Тем более что интерфейс реализован в минималистском стиле, чтобы исключить излишнюю неопределенность в выборе вариантов преобразований. Головная форма подсистемы «Алгебраист» содержит три текстовых окна и выпадающее меню. Два текстовых окна используются для ввода аргументов преобразований, третье – для вывода результата и формирования протокола решения задач. Результат в третьем окне фиксируется после каждого преобразования. Кроме того, в нем же сохраняется последовательность преобразований с указанием аргументов и результата. Последняя используется в случае, когда требуется совершить несколько взаимосвязанных преобразований с сохранением промежуточных результатов.
Выпадающее меню содержит все операции, которые могут использоваться в «Алгебраисте». Операции образуют полный базис, в том смысле, что он достаточный для решения задач по алгебре школьного курса. Выбирая последовательность необходимых преобразований, пользователь формирует искомое решение. Как уже было упомянуто, это решение сохраняется в протоколе и при завершении решения в базе данных.
Примеры использования системы «Алгебраист»
В этом разделе рассмотрим некоторые достаточно простые преобразования алгебраических выражений с использованием «Алгебраиста». Так как цель статьи состоит в концептуальном знакомстве с системой, то примеры выбраны, с одной стороны, достаточно наглядные, а с другой – простые с точки зрения поиска решения. При решении примеров используются лишь несколько наиболее типичных операций, чтобы дать общее представление о возможностях «Алгебраиста». Более комплексные примеры будут приведены в последующих публикациях.
Пример 1. Первым преобразованием будет упрощение выражения (a-b)(a2 + ab +b2). На головной форме в окне первого аргумента вводится выражение (a-b)(a^2 + ab + b^2), а в выпадающем меню выбирается пункт Упростить. Тот же результат будет получен, если в одном текстовом окне для ввода аргумента ввести выражение a-b, в другом – a^2 + ab + b^2 и выбрать пункт Умножить выпадающего меню. В обоих случаях результатом будет выражение a^3 – b^3.
Теперь проиллюстрируем работу «Алгебраиста», выполняя обратную операцию – деления многочленов. В первом случае вводим в первом текстовом окне аргумент a^3 – b^3, во втором – a – b и выбираем пункт Разделить выпадающего меню. В результате получаем выражение a^2 + ab + b^2. Если теперь в качестве аргументов ввести a^3 – b^3 и a^2 + ab + b^2, и в выпадающем меню вновь выбрать Разделить, то получим a – b. Тем самым, действие умножения многочленов проверено делением произведения на оба сомножителя.
Все результаты сохраняются в третьем текстовом окне в виде последовательности строк: два аргумента и результат. Кроме того, протокол решения сохраняется в базе, чтобы можно было использовать результаты вычислений для последующего анализа. Последнее очень важно, когда преподаватель разбирает ранее решенные задачи. Так как в протоколе приводятся лишь существенные моменты решения, он позволяет повысить эффективность обучения, избавляя от несущественных деталей. Кроме того, протокол содержит решенные ранее задачи и поэтому при повторении позволяет легко восстановить основную нить рассуждения.
Хотя скорость алгебраических преобразований в «Алгебраисте» вполне приличная, чтобы легко решать вновь введенные задачи, сохранение решений особенно полезно, когда приходится вводить длинные выражения. Действительно, легче просмотреть уже полученное решение, нежели вводить аргументы заново. Кроме того, сохраненные решения вполне подходят для самостоятельной проработки учащимися в точности так, как это делается в решебниках.
Алгебраические преобразования необходимы для решения нестандартных уравнений, когда приходится проводить предварительные преобразования, чтобы свести исходное уравнение к нескольким стандартным. Следующие два примера – решение таких уравнений. Демонстрируются возможности «Алгебраиста» по преобразованию уравнений, что позволяет свести нестандартные уравнения к стандартным.
Пример 2. Решить уравнение
x3 + x2 +3x = 5.
В текстовом окне для ввода аргумента вводим выражение x^3 + x^2 + 3x – 5 и воспользуемся пунктом меню «Найти делители». В результате исходное выражение раскладывается в произведение (x-1)(x^2+2x+5) двух выражений. Тогда исходное уравнение преобразуется в такое: (x-1)(x^2+2x+5) = 0, что равносильно решению двух уравнений: x-1=0 и x^2+2x+5 = 0. Первое из них имеет единственный корень 1, второе корней не имеет. Окончательный ответ: уравнение имеет единственный корень 1.
Пример 3. Решить уравнение
x (x+1)2 + (x+1) x2 = 30.
В текстовом окне для ввода аргумента вводим выражение x(x+1)^2 + (x+1)x^2 и воспользуемся пунктом меню «Упростить». Результат выглядит так: 2x^3+3x^2+x. Далее вводим выражение 2x^3+3x^2+x–30 и выбираем пункт: «Найти делители». В результате получаем произведение (x-2)(2x^2+7x+15). Следовательно, исходное уравнение сводится к двум уравнениям: x- 1 = 0 и 2x^2+7x+15 = 0. Первое уравнение имеет единственный корень: 1, второе корней не имеет. Окончательный ответ: уравнение имеет единственный корень 1.
Следующие два примера взяты из [5]. С технической точки зрения поиска решения в этих задачах вопросов нет. Однако в результате преобразований возникают длинные выражения, в которых ученики, как правило, по невнимательности часто допускают ошибки. Система «Алгебраист» избавляет от этого, повышая эффективность образовательного процесса.
Пример 4. Упростить выражение (1).
Система «Алгебраист» предоставляет возможности для всех преобразований этого примера. В частности, для получения окончательного результата выполняем следующие действия.
Приводим первую скобку к общему знаменателю (умножение, приведение подобных членов, упрощение). Общий знаменатель есть результат перемножения трех алгебраических выражений. Числитель – результат упрощения достаточно длинного выражения (умножение, приведение подобных членов, упрощение). После упрощения и сокращения получаем, что числитель и знаменатель результирующего выражения совпадают, но отличаются знаками. Поэтому первая скобка равна -1. Преобразования второй скобки выполняются аналогично, результат равен 1. Следовательно, окончательный ответ -1.
Такое несколько подробное изложение последовательности преобразований приведено исключительно с целью представить основные возможности «Алгебраиста» при решении задач упрощения.
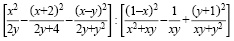 (1)
(1)
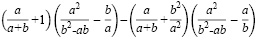 (2)
(2)
Пример 5. Упростить выражение (2).
Этот пример также решается применением стандартных преобразований. Все они поддерживаются в «Алгебраисте», избавляя школьника и преподавателя от рутинной работы по переписыванию выражений. В результате эффективность освоения нового материала и закрепление уже пройденного путем решения задач возрастает.
Как следует из описаний решений последних примеров, с помощью «Алгебраиста» они решаются с легкостью, избавляя ученика от ошибок, возникающих из-за невнимательности при переписывании длинных выражений. Преподавателю же предоставляется возможность ускорить прохождение материала, исключая рутинную работу и останавливаясь только на ключевых моментах.
Заключение
Программная система «Алгебраист» предоставляет возможность осуществлять все алгебраические преобразования в объеме средней школы. Тем самым система обладает достаточным функционалом и вполне может использоваться для подготовки школьников к ЕГЭ и олимпиадам по математике. «Алгебраист» является подсистемой более объемной системы «Живая математика» [1], она реализована на языке Python и обладает вполне приемлемым интерфейсом и естественным языком для описания алгебраических выражений. Приведено несколько примеров использования «Алгебраиста», демонстрирующих его возможности, вполне достаточные для решения в том числе олимпиадных задач. При решении уравнений и задач с параметрами алгебраические преобразования, предоставляемые «Алгебраистом», могут использоваться во взаимодействии с подсистемой «Графика» общей системы «Живая математика». Так, например, в результате соединения алгебраических возможностей и графической иллюстрации возникает более полное представление о том, какими решениями обладает уравнение. Это существенно сокращает время на поиск самого решения.

