Подготовка высококвалифицированных специалистов является важной составляющей любой образовательной программы высшего образования [1]. Она направлена на формирование у обучающихся навыков применения теоретических знаний в конкретных производственных ситуациях. В этой связи особое значение приобретает практико-ориентированный подход, который должен применяться в образовательном процессе как приоритетный [2]. Большая часть задач в области экономики связана с применением современного математического аппарата. Если проанализировать математическую компоненту в профессиональной деятельности специалиста в экономической области, то можно сделать вывод о том, что математическая подготовка является неотъемлемой составляющей подготовки выпускника к будущей профессиональной деятельности. Так, образовательная программа бакалавриата по направлению подготовки 38.03.01 Экономика содержит следующие математические дисциплины: алгебра, математический анализ, дифференциальные и разностные уравнения, теория вероятностей, математическая статистика, теория игр. Кроме этого, при решении экономических задач широко используются эконометрические методы: регрессионный анализ, трендовый анализ, анализ временных рядов, что также нашло свое отражение в образовательной программе посредством включения дисциплины «Эконометрика». Качественная математическая подготовка является необходимым условием для успешного освоения экономических дисциплин в дальнейшем. Это влечет за собой необходимость применения практико-ориентированного подхода при реализации образовательной программы бакалавриата по направлению подготовки 38.03.01 Экономика.
Цель исследования – разработка практико-ориентированных задач с прикладным экономическим содержанием по дисциплине «Математический анализ».
Материалы и методы исследования
Материалы исследования: федеральный государственный образовательный стандарт высшего образования и образовательный стандарт РАНХиГС по направлению подготовки 38.03.01 Экономика, рабочая программа дисциплины, результаты текущего контроля успеваемости обучающихся по дисциплине, личные разработки автора по дисциплине. Методы исследования: теоретические (анализ педагогической литературы, анализ нормативных документов) и эмпирические (наблюдение, анкетирование).
Результаты исследования и их обсуждение
Рассмотрим возможности использования практико-ориентированных задач в процессе обучения будущих экономистов на примере дисциплины «Математический анализ». Согласно образовательному стандарту РАНХиГС дисциплина «Математический анализ» обеспечивает формирование следующей обязательной профессиональной компетенции ПКо ОС II -1 «Способен использовать методы математического анализа для решения прикладных задач» [3, с. 45]. Таким образом, обучающийся должен не только знать понятийный аппарат, основные теоретические положения по дисциплине, но также уметь применять приобретенные знания при решении конкретных экономических задач. Математический аппарат не должен существовать отдельно, а должен быть частью общей реальной действительности, в том числе и профессиональной.
Ни для кого не секрет, что обучающиеся нематематических направлений подготовки сталкиваются с серьезными трудностями при изучении математических дисциплин. Это прежде всего связано со спецификой самой предметной области, а также и с методическими подходами к ее преподаванию. Преподавание математических дисциплин, с одной стороны, должно быть достаточно естественным, понятным (с точки зрения построения учебной дисциплины в целом), а с другой стороны, должно основываться на уровне разумного теоретического подхода [4]. При этом необходимо соблюдать все требования, которые предъявляются к уровню подготовки выпускника в соответствии с нормативными требованиями. Поэтому, чтобы процесс обучения по математическим дисциплинам положительно влиял на уровень профессиональной подготовки будущих выпускников, необходимо: направить изучение математических дисциплин на решение практико-ориентированных задач; показать связь математических понятий и теоретических положений с задачами экономического характера; повысить мотивацию обучающихся при изучении математических дисциплин с помощью включения в образовательный процесс задач с прикладным экономическим содержанием; усилить связь математических дисциплин с будущей профессиональной деятельностью обучающихся.
Рассмотрим некоторые примеры практико-ориентированных задач, которые могут быть использованы преподавателем в образовательном процессе при изучении дисциплины «Математический анализ».
Так, при изучении темы «Числовые последовательности» наглядным примером может служить исчисление конечных сумм денежных средств, находящихся во вкладах, путем исчисления процентов. Данные примеры иллюстрируют хорошо известные из курса средней школы числовые последовательности: арифметическую и геометрическую прогрессии.
Пример 1. Простая процентная ставка
.
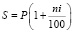P – сумма вклада, i – процентная ставка, n – число лет, S – наращенная сумма, S = P + I, I – проценты. Зависимость наращенной суммы S от времени n описывается линейной функцией. Зачастую начисление процентов осуществляется только по истечении ряда лет. В этом случае наращенная сумма S является арифметической прогрессией
,
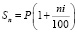первый член которой S1 равен P, а разность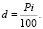 
Пример 2. Сложная процентная ставка
.
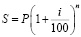В данном случае зависимость наращенной суммы S от времени n описывается показательной функцией. Если начисление процентов производится по истечении ряда лет, то наращенная сумма S есть геометрическая прогрессия
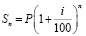
с первым членом S1 = P и знаменателем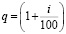 
.
Изучая тему «Предел и непрерывность функции», можно рассмотреть понятие непрерывности функции, точек разрыва, используя функциональные зависимости, встречающиеся в экономических исследованиях. При решении экономических задач встречаются как непрерывные функции, так и функции, имеющие разрыв. Приведем некоторые примеры таких функций.
Пример 3. N – налоговая ставка, Q – годовой доход, N = N(Q). График данной функции имеет схематично следующий график (рис. 1).
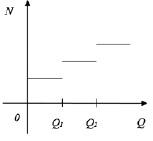
Рис. 1. График функции N = N(Q)
Из графика функции налоговой ставки следует, что функция N = N(Q) имеет точки разрыва (первого рода).
Пример 4. P – величина подоходного налога, Q – годовой доход, P = P(Q) –непрерывная функция. График данной функции изображен на рис. 2.
Функция, изображенная на рис. 2, является непрерывной функцией. С экономической точки зрения это означает, что если доходы за год отличаются незначительно у двух людей (ΔQ→0), то незначительно отличаются и их подоходные налоги (ΔP→0).
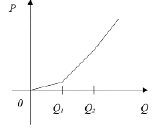
Рис. 2. График функции P = P(Q)
Классическими примерами непрерывных функций в экономике также могут служить функции спроса и предложения, где независимой переменной является цена.
Рассматривая темы «Производная и дифференциал функции», «Исследование свойств функций и построение их графиков», следует привести примеры использования функций из экономической области, таких как функция полезности, одноресурсная производственная функция, функция издержек производства, функция потребления и сбережения и др. Данные задачи хорошо иллюстрируют понятие производной функции, правила дифференцирования, логарифмическое дифференцирование, экономический смысл производной, нахождение экстремумов функции и др.
Пример 5. Пусть функция полезности для потребителя задается следующим соотношением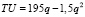 
.
Требуется определить значение переменной q, при котором общая полезность TU достигает своего максимального значения, а потребитель – насыщения.
Решение. Функция TU достигает максимального значения при условии, когда предельная полезность MU = 0, где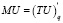 
.
Тогда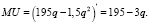 
Так как MU = 0, следовательно, 195 – 3q = 0, q = 65.
Таким образом, при данном значении переменной q функция общей полезности TU достигает своего максимального значения, а потребитель – насыщения.
Ответ. При q = 65 общая полезность является максимальной, и потребитель достигает насыщения.
Пример 6. Пусть u (усл. ед.) – объем продукции, которую выпускает крупный завод некоторого региона в течение рабочего дня, описывается следующим соотношением
,
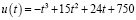где t(ч) – время.
Требуется определить: а) производительность труда; б) скорость изменения производительности труда; в) темп изменения производительности труда.
Определить указанные показатели в начале рабочего дня (t = 1), в середине рабочего дня (t = 4) и в конце рабочего дня (t = 7).
Решение. а) Из экономического смысла производной следует, что производительность труда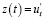 
. Для заданной производственной функции:
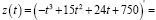
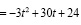(усл. ед./ч).
В заданные моменты времени получим: z(1) = 51, z(4) = 96, z(7) = 87.
Таким образом, на основе проведенных расчетов можно сделать вывод о том, что к концу рабочего дня происходит снижение производительности труда.
б)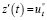 
– скорость производительности труда. Следовательно,
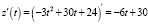(усл. ед./ч2).
В заданные моменты времени получим: z’(1) = 24, z’(4) = 6, z’(7) = –12.
Итак, изменение скорости производительности труда с плюса на минус означает, что рост производительности труда в начале рабочего дня меняется его снижением к концу рабочего дня.
в)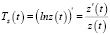 
– темп изменения производительности труда. Находим 
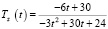(усл. ед./ч). Тогда в заданные моменты времени получим
Tz(1) = 8/17, Tz(4) = 1/16, Tz(7) = –4/29.
Полученные расчеты темпов изменения производительности труда позволяют еще раз подтвердить выводы, сделанные выше.
Ответ. а) производительность труда: z(1) = 51, z(4) = 96, z(7) = 87; б) скорость изменения производительности труда: z’(1) = 24, z’(4) = 6, z’(7) = –12; в) темп изменения производительности труда Tz(1) = 8/17, Tz(4) = 1/16, Tz(7) = –4/29.
Рассмотренный выше пример можно использовать при изучении темы «Производные высших порядков», так как скорость производительности труда является производной второго порядка от производственной функции (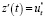
).
Пример 7.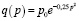 
, p0 > 0 – функция спроса от переменной p, где p – цена. Требуется определить такие значения p, при которых спрос является эластичным, нейтральным и неэластичным.
Решение. Эластичность функции определяется следующим образом:
.
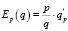В нашем случае:
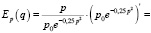
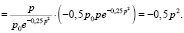
При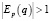 
спрос будет эластичным.
Следовательно,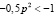 
, 
, 
.
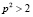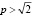При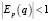 
спрос будет неэластичным.
Следовательно,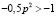 
, p2<2 , 
.
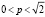При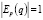 
спрос будет нейтральным.
Следовательно,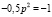 
, p2 =2 , 
.
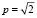Ответ. При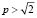 
спрос будет эластичным; при 
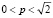спрос будет неэластичным; при 
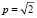спрос будет нейтральным.
Пример 8. Дана зависимость между себестоимостью продукции C и объемом производства Q, которая выражается соотношением C = 30 – 0,4Q.
Чему равна эластичность себестоимости C, если объем производства Q = 15?
Решение. Коэффициент эластичности себестоимости C рассчитывается по формуле
.
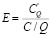Для нашей функции коэффициент эластичности равен
.
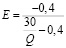Тогда при объеме производства Q = 15,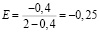 
.
Ответ. Эластичность себестоимости C составит –0,25.
Пример 9. Дана функция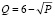 
, где Q – спрос за сутки на лимонад (тыс. шт.), P – цена за одну бутылку (руб.). Эффективная область работы формулы – от 1 до 25 рублей. При какой цене P за бутылку лимонада общая выручка будет наибольшей?
Решение.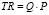 
– совокупная выручка. Для нашей задачи: 
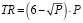. Следовательно, необходимо найти наибольшее значение данной функции на отрезке [1,25].
Вычислим стационарные точки:
, 
, 
, 
, 
.
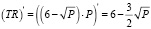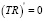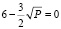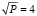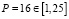Стационарная точка P = 16. На концах отрезка и в стационарной точке найдем значение функции совокупной выручки:
;
;
.
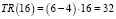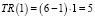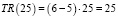Таким образом, совокупная выручка будет наибольшей, если цена за бутылку лимонада составит 16 руб.
Ответ. 16 руб.
Рассмотрим применение функции Кобба – Дугласа при изучении темы «Определенный интеграл». Предлагаемые задачи хорошо иллюстрируют основные понятия и используемые методы по данной теме.
Пример 10.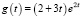 
– функция Кобба – Дугласа в предположении, что затраты труда есть линейная зависимость от времени, а затраты капитала неизменны. Требуется рассчитать объем произведенной продукции за 3 года.
Решение. С учетом сделанных предположений, объем произведенной продукции Q вычисляется по формуле
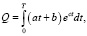
где T – количество лет.
Для нашей функции:
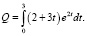
Вычислим интеграл:
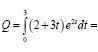
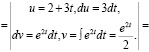
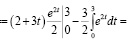
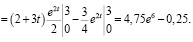
Ответ. Объем продукции, произведенной за 3 года, составит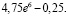 
Рассмотренная в статье тематика практико-ориентированных заданий не ограничивает применение методов математического анализа при решении задач профильной направленности [5]. Практико-ориентированные задания полезны для развития навыков анализа и диагностики экономических процессов, а также применения математических методов для прогнозирования экономических изменений и поиска оптимальных решений. Кроме того, такие задания могут помочь обучающимся развить собственные навыки решения задач, которые необходимы для работы в экономической сфере.
Данный подход применялся в 2021–2022 учебном году в процессе изучения дисциплины «Математический анализ» для обучающихся первого курса по направлению подготовки 38.03.01 Экономика Дальневосточного института управления – филиала РАНХиГС. В начале учебного года было проведено анкетирование обучающихся, в ходе которого было выяснено, что 70 % обучающихся не понимают, зачем будущему экономисту нужна математика. В качестве основной причины отмечалось то, что в школьном курсе математики не рассматривались вопросы применения математики в других областях и в экономике в частности. При изучении дисциплины «Математический анализ» практико-ориентированные задания использовались при проведении практических занятий, при выполнении домашних заданий, а также при проведении текущего контроля успеваемости обучающихся. Согласно рабочей программе дисциплины «Математический анализ» применялись следующие методы текущего контроля успеваемости обучающихся: контрольная работа, опрос. В рамках их проведения предлагались не только задачи из предметной области, но и практические задачи профильной направленности. После изучения дисциплины было проведено повторное анкетирование обучающихся, и уже только 20 % обучающихся затруднялись с ответом на поставленный вопрос, что свидетельствует о положительной динамике и эффективности применения рассматриваемого подхода автора.
Заключение
Таким образом, практико-ориентированные задачи являются эффективным средством оттачивания математических навыков и способностей, необходимых для успешного изучения экономических дисциплин в дальнейшем. Практико-ориентированные задачи являются важным компонентом математической подготовки будущих специалистов в экономической сфере. Представленный в статье подход, по мнению автора, позволит в наиболее полной мере обеспечить подготовку выпускников к профессиональной деятельности в соответствии с предъявляемыми нормативными требованиями.