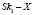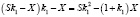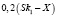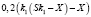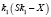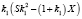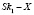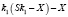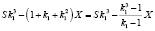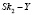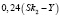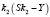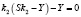Scientific journal

International Journal of Experimental Education

ISSN 2618–7159

ИФ РИНЦ = 0,425

Начнем свою работу с высказывания известного педагога-математика Д. Пойа: «Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности» [1].

Экономические задачи введены в базу КИМ профильного уровня ЕГЭ по математике сравнительно недавно – в 2015 году. Задачи этого типа по своей сложности входят в повышенный уровень и оцениваются с 2022 года двумя первичными баллами [2]. По данным статистики (за последние 3 года) ЕГЭ по математике (профильный уровень), правильно решили задание № 15 в 2020 году 22,0% выпускников, в 2021 году – 19,0%, в 2022 году – 34,1%, что указывает на нестабильную динамику.

Статистика анализа решения задач дает невысокий уровень доведения их до логического ответа. Это объясняется относительной сложностью задания для выпускников и тем, что элементарно решения чисто экономических задач нет в учебниках по алгебре, входящих в Федеральный перечень учебников РФ [3]. Основная трудность состоит, как нам кажется, в том, что обучающийся пока не сталкивался с кредитами и кредитными ставками, с вкладами и ставками по ним. Это во многом отражается на восприятии текста задачи и сформулированного в задаче вопроса. Экзаменуемый должен суметь выбрать оптимальный подход. В процессе работы и разбора типовых задач с учениками, посещающим дополнительные занятия, и учащимися Образовательного центра «Антарес» появилась идея написания статьи, которая, на наш взгляд, окажет помощь учителям школ в процессе подготовки учащихся к ЕГЭ по математике (профиль).

Цель исследования – способствовать формированию фундаментальных знаний у будущих участников ЕГЭ посредством изучения методов решения практико-ориентированных задач экономического содержания профильного экзамена по математике.

Материал и методы исследования

Широкое использование математических размышлений во множестве современных процессов и изменений, происходящих в нашем обществе, позволяет расширить роль математики в современных условиях.

Формы, методы и методики проведения ЕГЭ по математике подвержены изменениям. В школьных учебниках практически отсутствуют задания по применению математических знаний в экономике, поэтому трудно предположить, что обучавшиеся, подготовка которых к государственной аттестации не содержала «экономического тренажа», смогут в атмосфере организации и проведения ЕГЭ успешно справиться с подобными задачами.

При решении задач с экономическим содержанием следует вникнуть в условие задачи; выразить основные действия в условии на математическом языке; выполнить действия; изучить полученное решение (взгляд назад) [4].

Расчеты по получению кредитов обычно сводятся к одному из двух характерных типов задач, которые легко различить между собой.

1. Выплаты кредита производятся равными платежами (аннуитетными платежами). В силу громоздкости вычислений в задачах этого типа иногда применяется формула суммы n первых членов геометрической прогрессии.

Задача 1. После первого полугодия 2023 года бизнесмен планирует взять кредит в Сбербанке на некоторую сумму. Банк предложил бизнесмену два варианта кредитования:

1-й вариант

– кредит предоставляется на три календарных года;

– в конце февраля каждого года действия кредита долг увеличивается на 20% от суммы долга на конец предыдущего года;

– в период с марта по июнь каждого года действия кредита выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью

2-й вариант

– кредит предоставляется на два календарных года;

– в конце февраля каждого года действия кредита долг увеличивается на 24%;

– в период с марта по июнь каждого года действия кредита выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью

Когда бизнесмен подсчитал, то выяснил, что по 2-му варианту кредитования ему придется выплачивать на 373 600 рублей меньше, чем по 1-му варианту. Какую сумму бизнесмен планирует взять в кредит?

Решение. Пусть S – сумма кредита, X – платежи по первому варианту, а годовые составляют r1 = 20%. Тогда в конце февраля каждого года оставшаяся сумма долга умножается на коэффициент 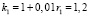, так как

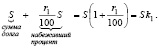
Для нахождения ежегодной выплаты по 1-му варианту кредитования целесообразно составить таблицу 1.

Таблица 1

Ежегодная выплата по 1-му варианту кредитования

Так как по условию:

,

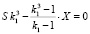то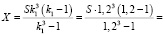

.

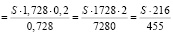Таблица 2

Ежегодная выплата по 2-му варианту кредитования

Пусть теперь Y – платежи по 2-му варианту, а годовые по 2-му варианту составляют r2 = 24%. Тогда в феврале каждого года оставшаяся сумма долга умножается на коэффициент 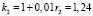. Аналогично 1-му варианту кредитования составим таблицу 2.

Рассуждая аналогично, находим, что, если бы долг бизнесмен гасил двумя равными выплатами, то ежегодная выплата была бы равной:

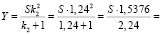
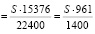рублей.

Разность величин выплат между тремя и двумя аннуитетными платежами:

.

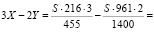
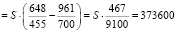Откуда S = 7280000.

Ответ: 7280000.

Основной проблемой в решении таких задач становятся вычислительные ошибки. Решая задачи экономического содержания, иногда целесообразно переходить от десятичной дроби к обыкновенной дроби, чтобы минимизировать ошибки вычислительного характера.

Задача 2. В июле Яна планирует взять кредит на три календарных года на целое число миллионов рублей. Два банка предложили Яне оформить кредит на следующих условиях:

– в январе каждого года действия кредита долг увеличивается на некоторое число процентов (ставка плавающая – может быть разной для разных годов);

– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причем последний платеж должен погасить долг по кредиту полностью.

В первом банке процентная ставка по годам составляет 10, 20 и 15 процентов соответственно, а во втором – 15, 10 и 20 процентов. Яна выбрала наиболее выгодное предложение. Найдите сумму кредита, если эта выгода по общим выплатам по кредиту составила от 14 до 15 тысяч рублей.

Решение. Пусть сумма кредита Яны составляет S млн рублей, а ежегодные выплаты в первом банке – X млн рублей. По условию, долг перед первым банком (в млн рублей) по состоянию на июль должен уменьшаться согласно ряду:

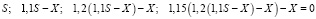или

,

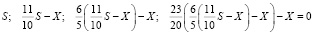откуда .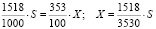

Пусть ежегодные выплаты во втором банке составляют Y млн рублей. По условию, долг перед вторым банком (в млн рублей) по состоянию на июль должен уменьшаться согласно ряду:

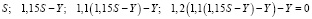или

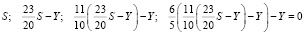, откуда

.

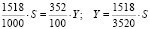Заметим, что общие выплаты по кредиту в первом банке меньше, чем во втором. Поэтому:

,

,

.

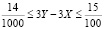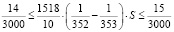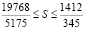Получаем S = 4 млн рублей.

Ответ: 4000000.

2. Выплаты кредита подбираются так, что сумма долга уменьшается по равномерному закону. Это так называемая схема с дифференцированными платежами. В задачах этого типа мы часто сталкиваемся с формулами суммы конечного числа членов арифметической прогрессии.

Задача 3. В июле 2025 года планируется взять кредит в банке на некоторую сумму на 10 лет. Условия его возврата таковы:

– в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 18% по сравнению с концом предыдущего года;

– в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;

– с февраля по июль каждого года необходимо выплатить часть долга;

– в августе каждого года долг должен быть на одну и ту же величину меньше долга на август предыдущего года;

– к августу 2035 года кредит должен быть полностью погашен.

Найдите общую сумму выплат полного погашения кредита.

Решение. Пусть сумма кредита составляет S тыс. рублей.

По условию, долг перед банком (в тыс. рублей) по состоянию на август 2025–2035 годов должен уменьшаться до нуля следующим образом:

.

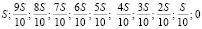В январе каждого года с 2026 по 2030 долг возрастает на 18%, а в январе каждого года с 2031 по 2035 – на 16%, значит, последовательность размеров долга (в тыс. рублей) в январе 2026–2035 годов такова:

.

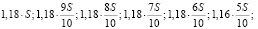
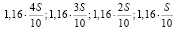Следовательно, выплаты (в тыс. рублей) должны быть следующими:

.

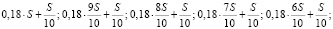
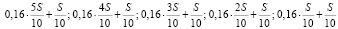Значит, сумма всех выплат (в тыс. рублей) по данному кредиту равна:

.

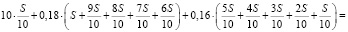
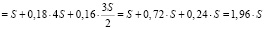Откуда 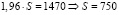, то есть сумма всех выплат составила 750 тыс. рублей.

Ответ: 750000.

Таблица 3

Таблица всех выплат и долга

Среди задач встречаются такие, при решении которых требуется подсчитать сумму, выплаченную за определенный период срока кредитования.

Задача 4. 15 января текущего года клиент взял кредит в банке на два календарных года. В договоре кредитования прописано:

– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;

– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Сколько рублей нужно клиенту будет вернуть банку за весь срок кредитования, если за пятнадцатый месяц выплата составляет 44 тыс. рублей?

Решение. Пусть первоначальная сумма кредита равна S = 24X тыс. рублей. В течение 24 месяцев она равномерно уменьшается до нуля рублей. Без учета процентов ежемесячные выплаты составят: 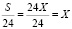тыс. рублей.

В данной задаче целесообразно составить таблицу всех выплат и долга (табл. 3).

По условию за 15-й месяц кредитования нужно выплатить 44 тыс. рублей, то есть:

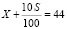; 110X = 4400;

X = 40; S = 24 ∙ 40 = 960 тыс. рублей.

Тогда всего следует выплатить банку:

.

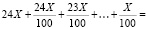
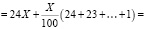
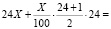
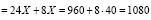Таким образом, общая сумма выплат после полного погашения кредита составит S1 = 1080 тысяч рублей, это сумма кредита плюс ежемесячные проценты.

Ответ: 1080000.

В контрольно-измерительных материалах ЕГЭ встречаются задачи, в которых долг уменьшается неравномерно, но известна закономерность его уменьшения.

Задача 5. В июле 2023 года клиент Сбербанка собирается оформить кредитование на три года в размере S млн рублей, где S ∈ Z. Условия договора таковы:

– каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;

– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

– в июле каждого года долг должен уменьшаться до нуля в соответствии со следующей схемой: S; 0,8S; 0,4S; 0.

Чему равно наибольшее значение S, при котором каждая из выплат будет меньше 5 млн рублей?

Решение. Долг перед банком (в млн рублей) на июль каждого года:

Согласно условию, наибольшая из выплат не должна превышать 5 млн рублей:

.

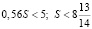Наибольшее целое число, удовлетворяющее этому неравенству, равно 8. Оно и определяет величину максимального кредитования.

Ответ: 8.

Экономические вопросы ЕГЭ включают в себя и задания нахождения оптимальных значений, решение которых требует не совсем стандартного подхода [5]. Задачи такого типа чаще всего решают с применением производной, но мы рассмотрим альтернативное решение.

Задача 6. В начале 2021 года предприниматель купил акции Газпрома за 11 тыс. рублей. Стоимость акций ежегодно возрастает на 4 тыс. рублей. В январе любого года предприниматель может продать акции и положить вырученные деньги на банковский счет (открыть вклад). Ежегодно сумма вклада будет увеличиваться на 10%. В начале какого года предприниматель должен продать акции, чтобы через 15 лет после покупки сумма вклада была наибольшей?

Решение. Пока предприниматель не продал акции, величина их стоимости ежегодно увеличивается на 4 тыс. рублей. Через n лет их стоимость будет равна 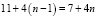тыс. рублей.

Продажа акций Газпрома через n лет после покупки и открытия банковского вклада будет обеспечивать повышение величины вклада ежегодно на 10% (то есть в 1,1 раза) в течение 15 – n лет.

Значит, через 15 лет после приобретения акций величина вклада равна .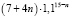

Нам нужно найти номер максимального члена последовательности 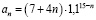, где .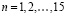

Рассмотрим разность

,

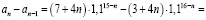
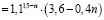отсюда 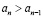при n ≤ 9 и 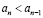при n > 9.

Таким образом, наибольшее значение последовательность an принимает при n = 9.

Значит, акции надо продать на девятый год после их приобретения, т.е. в 2029 году.

Ответ: 2029.

Все рассмотренные задачи в полной мере соответствуют рекомендациям по подготовке к единой по РФ аттестации выпускников школ и взяты из сборника ФИПИ ЕГЭ-2023 профильного уровня под редакцией И.В. Ященко [6].

Результаты исследования и их обсуждение

По теме исследования изучены некоторые подходы к решению экономических задач, которые позволяют при построении математической модели избегать ошибок вычислительного характера, сосредоточиться на выборе решения по типу задач. Приступая к выполнению задания под № 15 (после проведенных занятий), малое число обучающихся составляют неверную модель, некоторые допускают арифметические ошибки при работе с правильно составленной моделью, а подавляющее большинство (в том числе учащиеся 10-го класса Образовательного центра «Антарес»), нашедшие путь решения, верно доводят его до конца, что указывает на рост математической культуры. При этом хочется отметить, что многие из участников эксперимента предпочли комбинировать методы решения во избежание вычислительных ошибок и с целью экономии времени.

Выводы

Методы решения задач экономического характера вызывают интерес к прикладным задачам и математике в целом. Выпускники школ, которые способны решать экономические задачи, успешнее справляются с другими заданиями ЕГЭ.