Введение
В современном обществе математика играет все более важную роль. Ее применение в различных сферах жизни помогает лучше понимать и объяснять происходящие процессы. Помимо общей грамотности необходима также элементарная математическая грамотность. Учащиеся должны уметь использовать как традиционные, так и инновационные методы. Д. Пойа отмечал, что поиск правильного решения задачи – это творческий процесс, который можно сравнить с искусством [1, с. 15]. Умение применять как классические подходы, так и нестандартные способы решения задач поможет учащимся в их дальнейшей научно-исследовательской работе.
Неравенства играют ключевую роль в различных областях современной математики. Без них невозможно представить себе ни физику, ни математическую статистику, ни экономику. Несмотря на широкое использование неравенств, до сих пор не существует единой и хорошо разработанной теории, которая могла бы охватить все их разновидности. Однако для некоторых классов неравенств такая теория уже была создана. Неравенства можно встретить как в классических, так и в самых современных разделах математики.
Исследование неравенств является самым сложным разделом программного курса математики. Умение решать неравенства обязательно учитывается при итоговой аттестации учащихся [2, c. 204]. Традиционно неравенства вызывают у учащихся наибольшие трудности. Они не только не понимают логику их исследования, но и затрудняются в выборе метода решения. В отличие от уравнений, в неравенствах невозможно проверить найденные решения. Поэтому стандартная схема решения уравнений, которая предполагает получение последовательности уравнений-следствий и отбор корней, не подходит для решения неравенств. Однако многие приемы и методы, используемые для решения неравенств, схожи с теми, что используются для уравнений.
Особую трудность представляют собой иррациональные неравенства. Ученик, видя в тексте задания корень любой степени, начинает испытывать страх от неумения или незнания использования свойств радикалов. Изучение неравенств открывает множество возможностей для формирования и развития математической культуры, позволяет использовать разнообразные педагогические методы для развития логического мышления. Практическое применение теоретических знаний напрямую зависит от уровня их усвоения [3, с. 107].
Классические методы требуют больших вычислений, поэтому в некоторых случаях более эффективным решением может быть использование нестандартных подходов к неравенствам, которые часто встречаются в олимпиадных задачах для школьников, а также во второй части КИМ ЕГЭ. Для успешной сдачи ЕГЭ очень важно правильно распределять время, поэтому требуются новые методы решения, обеспечивающие наиболее быстрое выполнение заданий. Чтобы использовать эти методы, нужно хорошо разбираться в таких понятиях, как функция и ее свойства, среднее арифметическое и геометрическое, а также быть знакомым с некоторыми тождествами.
Нестандартные методы, основанные на использовании известных численных неравенств, часто остаются в тени. Однако они могут быть очень эффективны при решении многих математических задач, особенно повышенной сложности. Поэтому незнание их может значительно ограничить количество успешно решаемых задач. Выполнение разнообразных заданий поможет развить логическое мышление и получить опыт работы с задачами повышенной сложности, выходящими за рамки обязательного уровня. Тогда основу подготовки школьников составит обучение предварительному анализу задачи [4, с. 282]. Это, в свою очередь, способствует формированию навыков познавательной активности, повышению математической культуры и расширению кругозора учащихся. Оптимизация поиска методов решения задач позволит учащимся достичь более высокого уровня подготовки к ЕГЭ.
Цель исследования – изучить нестандартные методы решения неравенств, базирующихся на использовании неравенств Коши и Бернулли.
Материалы и методы исследования
При подготовке статьи был проведен тщательный анализ научно-методической литературы, посвященной классическим неравенствам. Изучены нестандартные методы решения неравенств, базирующихся на использовании неравенств Коши и Бернулли. Приведены примеры, которые наглядно демонстрируют, что рассмотренные методы не требуют специальной подготовки и особых навыков. Они предполагают наличие умения обобщать и анализировать, а их использование значительно сокращает время и упрощает решение задач. Данным неравенствам в последние годы уделяется весьма существенный интерес. Однако их применение требует особого внимания, чтобы избежать возможных ошибок. Поэтому одной из задач учащихся является освоение нестандартных методов решения неравенств. Важно мотивировать учеников тем, что они смогут более уверенно и точно решать задачи с неравенствами на олимпиадах и получать больше баллов на ЕГЭ.
Результаты исследования и их обсуждение
В школьном курсе математики изучаются различные виды неравенств. Для их решения существует множество методов, среди которых особенно выделяются метод интервалов, метод замены переменной, метод рационализации и метод оценки. Суть метода рационализации при решении неравенств заключается в замене сложного выражения f(x) на более простое φ(x). При этом новое выражение f(x) < 0 должно быть равносильно φ(x) < 0 в области определения f(x). Чтобы использовать метод оценки для решения неравенств, необходимо, чтобы в неравенстве присутствовали функции разных типов, а также была возможность оценить одну часть неравенства. Чтобы эффективно применять эти методы, необходимо обладать определенными навыками и знаниями, которые позволят нам выстраивать логические цепочки рассуждений.
Отметим, что в рамках данной работы под термином «нестандартные методы» подразумеваются те, которые в настоящее время не являются широко распространенными в школьной литературе и не используются в школьной практике. Эти методы позволяют найти ответ быстрее, чем традиционные.
При изучении неравенств (в частности, иррациональных) и поиске их решений часто применяют неравенство Коши: A ≥ C, где A – среднее арифметическое, C – среднее геометрическое неотрицательных величин. Это позволяет значительно упростить процесс решения. В общем случае можно перейти как к среднему арифметическому, так и к среднему геометрическому. Известное неравенство Коши
,
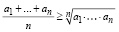которое справедливо для неотрицательных значений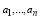 
, будем использовать в записи:
.
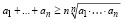Его часто используют для решения уравнений, доказательства неравенств и систем методом оценок. Задания с его применением встречаются в олимпиадах и на ЕГЭ; редко олимпиада обходится без задач, где требуется доказать определенное неравенство.
При доказательстве неравенств можно использовать различные методы и приемы. Иногда для получения нужного результата достаточно обратиться к определению неравенства, то есть рассмотреть разницу между левой и правой его частями. Также полезно использовать уже известные неравенства или оценивать обе части доказываемого неравенства. В некоторых случаях удается доказать неравенство, сведя его с помощью равносильных преобразований к очевидному (верному) неравенству.
Рассмотрим примеры, которые демонстрируют применение неравенства Коши.
Пример 1. Доказать, что
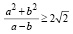, если ab = 1 и a – b > 0.
Доказательство. После выделения полного квадрата и выполнения ряда преобразований в левой части неравенства, учитывая условия ab = 1, a – b > 0, получим
.
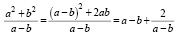Применив неравенство Коши для значения n = 2, получим
.
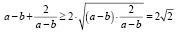Таким образом, неравенство доказано.
Пример 2. Доказать неравенство
,
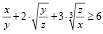где x > 0, y > 0 и z > 0.
Решение. Применим неравенство Коши для значения n = 6. Тогда получим
.
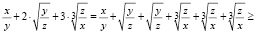
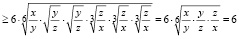Отметим, что доказанное неравенство можно обобщить на случай, когда его левая часть содержит n слагаемых. В такой ситуации имеет место
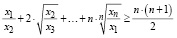, где n ≥ 1.
При значениях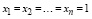 
в этом неравенстве достигается равенство.
Пример 3. Решите неравенство
.
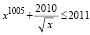Решение. Представив второе слагаемое левой части неравенства как сумму 2010 дробей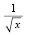 
, получим сумму из 2011 слагаемых. Полученную сумму, согласно неравенству Коши, заменим средним геометрическим:
.
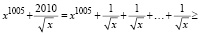
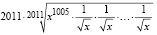В итоге приходим к следующему равносильному неравенству:
, 
, 
, 
.
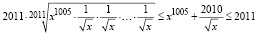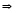
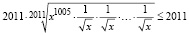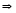
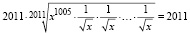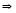
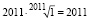Поскольку равенство среднего арифметического и среднего геометрического возможно только в случае, когда входящие в них элементы равны, то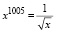 
, 
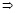x = 1.
Это решение является единственным, поскольку во всех других случаях, кроме x = 1, левая часть исходного неравенства будет больше правой.
Ответ. x = 1.
В инженерных задачах часто возникает необходимость сравнивать алгебраические выражения. Мощным инструментом, позволяющим находить оптимальные решения для таких задач, является использование неравенства Бернулли: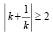 
.
Пример 4. Сравните значения
2 и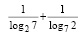 
.
Решение. По свойству логарифма, учитывая, что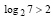 
, получим
.
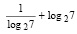Тогда согласно неравенству Бернулли:
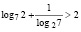, то есть 
.
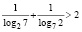Ответ.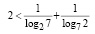 
.
Пример 5. Проверьте, выполняется ли неравенство:
.
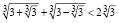Решение. Преобразуя левую часть неравенства, получим
.
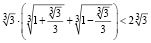Разделив на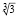 
обе части неравенства, имеем 
.
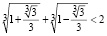Теперь применим неравенство Бернулли к левой части:
.
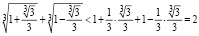Таким образом, исходное неравенство становится очевидным и выполняется.
Помимо «классического» неравенства Бернулли существует и менее известная формулировка этого математического соотношения:
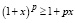, если p < 0 или p > 1;
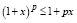, если 0 < p < 1.
Проиллюстрируем на примерах.
Пример 6. Сравните числа
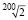и 1,006.
Решение. Возводя обе части формального неравенства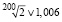 
в 200 степень, xполучим: 
.
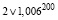Используя неравенство Бернулли, оценим правую часть:
.
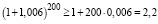То есть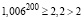 
.
Отсюда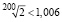 
.
Ответ.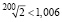 
.
Пример 7. Решить неравенство
.
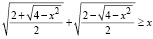Решение. ОДЗ в неравенстве являются –2 ≤ x ≤ 2. Так как неравенство выполняется при x = 0, то рассмотрим случай 0 < |x| ≤ 2.
Преобразуем неравенство в более удобную для сравнения форму:
.
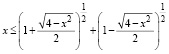Если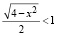 
, то 0 < |x| ≤ 2.
Применяя неравенство Бернулли к правой части равносильного неравенства, получим
.
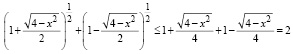Из этого вытекает неравенство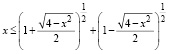 
. Получим x ≤ 2.
Таким образом, неравенство справедливо на всей ОДЗ, то есть решением данного неравенства являются –2 ≤ x ≤ 2.
Неравенство Бернулли также может быть использовано при решении уравнений, доказательстве тригонометрических неравенств и нахождении наибольшего значения функции.
Исследование показало, что для решения сложных задач не всегда возможно использовать стандартные методы. Поэтому важно уметь применять и нестандартные. Приступая к выполнению задания (после проведенных занятий), подавляющее большинство учащихся, нашедших путь решения, верно доводит его до конца, что указывает на рост математической культуры. Практическое решение неравенств нестандартными методами способствует развитию интуиции и улучшению логического мышления.
Заключение
Владение нестандартными способами решения задач позволяет значительно сократить время, необходимое для выполнения задания. В некоторых случаях это может быть единственным верным решением, что особенно важно при подготовке к ЕГЭ.
Таким образом, для целого ряда задач применение классических неравенств Коши и Бернулли позволяет с помощью несложных выкладок получить достаточно простые и доступные решения.