Введение
В последние годы процесс информатизации образования набирает все большие обороты, стимулируя создание новых технологий и методических систем обучения, направленных на развитие интеллектуального потенциала обучаемых [1]. В сфере математического образования активно внедряются электронные обучающие платформы и цифровые среды [2]. Одна из таких сред – информационно-образовательная среда Nomotex – была разработана на кафедре вычислительной математики и математической физики МГТУ им. Н.Э. Баумана и с 2016 года внедрена в учебный процесс для математической подготовки инженеров [3]. Цифровая среда Nomotex уже зарекомендовала себя в учебном процессе по различным математическим дисциплинам. В частности, на ее основе реализованы интерактивные курсы по дифференциальным уравнениям [1], аналитической геометрии и линейной алгебре [4], основам теории систем [2]. ИОС Nomotex обеспечивает генерацию заданий для контрольных и лабораторных работ, автоматическую проверку введенных студентами решений и детализированную обратную связь по результатам [4; 5].
Математическая статистика является дисциплиной, вызывающей у студентов определенные трудности восприятия, особенно без достаточной практики на реальных данных. По данным исследований, изучение статистики нередко воспринимается учащимися как сложное, а традиционные методы обучения могут быть малоэффективны, если студенты остаются пассивными [6]. Современные исследования подчеркивают, что непосредственная обратная связь и интерактивные цифровые инструменты способны существенно повысить успеваемость и мотивацию при изучении математических дисциплин [7; 8]. Так, систематический обзор показал, что почти в 2/3 исследований автоматизированная обратная связь приводила к улучшению результатов обучения студентов, не уступая по эффективности традиционной ручной проверке [7]. Особенно высокое влияние оказывает пошаговая интерактивная обратная связь, которая направляет обучаемого к верному решению задачи через серию подсказок или проверок после неудачных попыток. Такой формат способствует активному усвоению материала: студент получает указание на конкретный этап, где допущена ошибка, и может сразу скорректировать свое решение, что превращает процесс оценки в часть обучения. В результате возрастает вовлеченность учащихся и их стремление улучшить результат, а положительное влияние наиболее заметно у студентов с начальными трудностями [9].
Целью исследования было разработать и внедрить в ИОС Nomotex систему цифрового сопровождения лабораторных работ по математической статистике.
Материалы и методы исследования
Основная идея – автоматизировать проверку ключевых результатов, которые студенты получают в ходе выполнения лабораторной работы на компьютере, с использованием Mathcad, Python или других средств, и обеспечить мгновенную обратную связь по каждой контрольной точке решения. Контрольные точки были выделены на основе структуры задачи и включают такие результаты, как основные статистические показатели выборки, параметры распределения, значения статистических критериев и т.д. Такой подход позволяет оценивать не только итоговый ответ, но и ход решения студента, аналогично методикам, примененным в других курсах на платформе Nomotex [4]. Ожидается, что пошаговая проверка с указанием неверных значений поможет студентам лучше понять материал и избежать накопления ошибок, а также снизит нагрузку на преподавателя при проверке работ. Базой для эксперимента послужила информационно-образовательная среда Nomotex. Лабораторные работы проводились в смешанном формате, часть расчетов студенты выполняли самостоятельно с помощью вычислительных средств (Mathcad, Python) и параллельно вводили ключевые результаты в электронные формы Nomotex для проверки и получения подсказок. Каждому студенту автоматически выдавался индивидуальный вариант задания с уникальными исходными данными. Курс математической статистики предусматривал выполнение двух связанных между собой лабораторных работ.
Лабораторная работа 1. Статистическое исследование выборки и проверка гипотезы о распределении. Студент получает выборку объема ~100 из неизвестного непрерывного распределения. Требуется:
• выполнить группировку данных, число интервалов определить по правилу Стерджесса, построить гистограмму относительных частот;
• найти эмпирическую функцию распределения (ЭФР) и построить ее график;
• вычислить выборочное среднее Х и выборочную дисперсию S2;
• по виду гистограммы выбрать предположительный вид закона распределения генеральной совокупности. Оценить неизвестные параметры этого распределения;
• проверить соответствие выборки выбранному закону распределения с помощью критерия Пирсона на заданном уровне значимости α, сделать вывод о принятии или отклонении нулевой гипотезы H0.
Лабораторная работа 2. Доверительные интервалы для параметров нормального распределения. Студент получает выборку объема ~100, которая сгенерирована из нормального распределения (неизвестного среднего a и дисперсии σ2). Требуется:
• разбить выборку на интервалы по правилу Стерджесса (как в зад. 1) и вычислить частоты, построить гистограмму;
• вычислить выборочные среднее Х и дисперсию S2;
• наложить на гистограмму график плотности нормального распределения с параметрам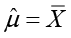и 
и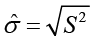 
(оценки по выборке);
• для доверительных уровней
1 – α = 0.90; 0.95; 0.99
определить доверительные интервалы: (a) для математического ожидания μ при неизвестной σ; (b) для среднего квадратического отклонения σ при неизвестном μ.
Каждая из этих лабораторных работ включала несколько этапов вычислений и построений. В традиционном формате проверка таких заданий отнимает значительное время у преподавателя, кроме того, студент не получает своевременной обратной связи о допущенных неточностях. Разработанный алгоритм цифрового сопровождения предназначен для преодоления этих ограничений.
Тестирование и внедрение разработанного алгоритма проводилось в течение второго семестра 2024-2025 года, а также в первом семестре 2025-2026 учебного года. В тестировании принимали участие студенты 8 групп Московского государственного технического университета имени Н.Э. Баумана факультета «Энергомашиностроение». В ходе тестирования были исправлены ошибки, связанные с неправильным ответом, указанным в системе для проверки, а также получена обратная связь от студентов и преподавателей, участвующих в тестировании.
Результаты исследования и их обсуждение
На платформе Nomotex для каждой лабораторной работы создан специальный модуль с пошаговыми интерактивными формами ввода. Решение студентом разделено на логические этапы, соответствующие пунктам методических указаний. После выполнения очередного шага студент вводит полученное значение в соответствующее поле в Nomotex. Система мгновенно проверяет введенное значение, сравнивая его с эталонным расчетным значением, вычисленным системой заранее или полученным из введенных ранее данных [7]. Если значение не совпадает, система выдает сообщение об ошибке с указанием, что значение рассчитано неверно, побуждая пересчитать его. Такая автоматическая проверка реализована для всех ключевых результатов: абсолютных частот, значений ЭФР в контрольных точках, выборочных статистик (Х, S2), оценок параметров распределения, теоретических частот, значения χ2 и т.д.
Nomotex берет на себя часть рутинных вычислений и построений, чтобы разгрузить студента от технической работы и позволить сосредоточиться на интерпретации результатов.
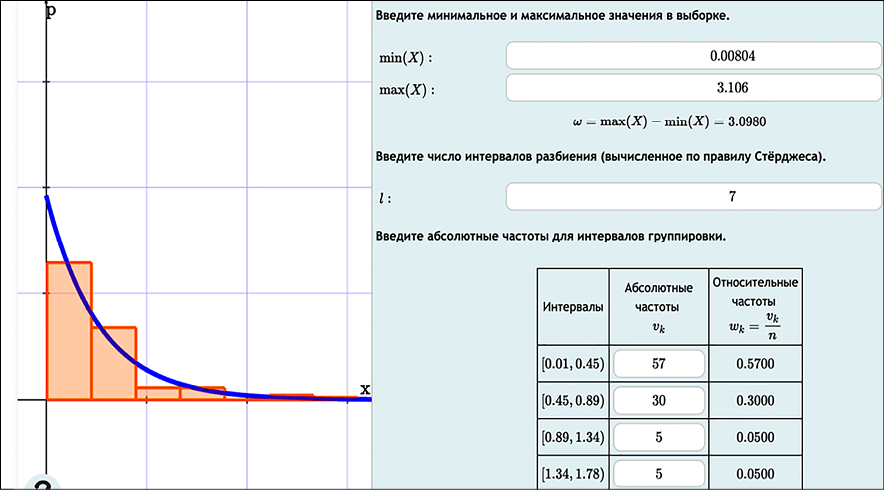
Интерфейс программного модуля для сопровождения лабораторных работ Примечание: составлено авторами
Например, студент вводит число интервалов m для группировки – система автоматически рассчитывает границы интервалов равной длины и отображает их. После того как студент введет абсолютные частоты по интервалам, Nomotex строит по ним гистограмму относительных частот (масштабируя частоты на единицу). Это избавляет от необходимости чертить гистограмму вручную и сразу дает корректное визуальное представление распределения данных. Аналогично, после ввода студентом оценок параметров предполагаемого закона распределения, Nomotex строит поверх гистограммы график плотности соответствующего распределения. Такая визуализация позволяет наглядно сопоставить эмпирическое распределение выборки с теоретической моделью и лучше понять характер отличий. На рисунке показан интерфейс разработанного программного модуля на платформе Nomotex, слева показана гистограмма, построенная по введённым значениям, справа – формы для ввода ключевых значений для лабораторной работы 1.
Как отмечают исследователи, гистограммы часто ошибочно воспринимаются студентами [10], поэтому интерактивные средства, позволяющие сразу увидеть эффект изменения параметров на форме плотности, чрезвычайно полезны в обучении.
Если на каком-либо шаге студент вводит неверное значение, система мгновенно сигнализирует об этом. Реализация сделана максимально простой: поля ввода имеют настройки допустимого диапазона и точности, а при несоответствии ответу выводится стандартное сообщение вроде «Введенное значение неверно, попробуйте еще раз». Однако даже такая простая индикация направляет студента к поиску ошибки. Например, если студент неправильно вычислил дисперсию S2, система сразу сообщит, что значение неверно – это заставит пересмотреть расчеты, вспомнить формулу. Это повышает качество усвоения, так как обратная связь приходит в момент выполнения задания, а не спустя долгое время после сдачи работы [8].
Внедрение разработанного алгоритма цифрового сопровождения позволило практически исключить случаи незавершенных или неверно выполненных лабораторных работ. Следует отметить, что особенно полезной оказалась визуализация гистограмм и наложенных плотностей. Многие студенты впервые строили гистограмму самостоятельно и без помощи системы могли допустить ошибки в масштабировании. Nomotex же автоматически масштабировала частоты в относительные величины, благодаря чему все гистограммы были построены правильно. Это, в свою очередь, позволило корректно подобрать вид распределения. По наблюдениям преподавателей, раньше часть студентов затруднялась по гистограмме отличить, например, равномерное распределение от нормального с большой дисперсией. Теперь же, когда поверх гистограммы сразу отображалась теоретическая кривая, выбор гипотезы значительно упростился. Студенты отмечали, что такой наглядный подход помог им лучше понять связь между выборочным распределением и теоретической моделью. Данное наблюдение согласуется с результатами обзора, указывающего на распространенные сложности в интерпретации гистограмм и важность наглядности для преодоления этих сложностей [10].
Анализ лог-файлов системы показал, что среднее число попыток ввода на один этап составляло 1.2–1.3, то есть в большинстве случаев студенты отвечали правильно с первой попытки, а если и ошибались, то быстро исправлялись. Важный качественный результат – практически все студенты воспользовались возможностью повторного ввода вместо того, чтобы останавливаться на неверном решении [11]. Иными словами, мгновенная обратная связь стимулировала их довести работу до правильного конца, вместо того чтобы сдавать работу с ошибками [12]. Это соответствует современным подходам к формативному оцениванию и адаптивному обучению, при которых система наставляет обучаемого в процессе решения задачи [9].
Применение Nomotex для сопровождения лабораторных работ существенно упростило контроль и оценивание. Преподавателю больше не требовалось вручную проверять каждое расчетное значение в тетрадях – система сделала это в автоматическом режиме. Объективность оценки при этом повысилась, критерии оценивания стали полностью прозрачны и единообразны, поскольку заложены в алгоритм [13]. Это аналогично практике в курсах высшей математики на Nomotex, где автоматическая проверка учитывает все возможные правильные варианты и оценивает не только ответ, но и ход решения, выделяя контрольные точки [4]. Более того, Nomotex накопила данные о попытках студентов, что позволило преподавателю проанализировать типичные затруднения и скорректировать объяснения на последующих занятиях. Например, увидев, что у значительной части группы возникли ошибки при определении числа степеней свободы для критерия χ2, преподаватель уделил этому вопросу дополнительное внимание на семинаре. Таким образом, цифровое сопровождение дало не только оперативную обратную связь студентам, но и ценную обратную связь преподавателю о том, какие темы вызывают сложности [11].
Полученный опыт соотносится с результатами других работ по цифровой трансформации математического образования [14]. Отмечается, что применение автоматизированных обучающих систем с интерактивной обратной связью ведет к росту успеваемости и не уступает традиционным методам при значительно большем охвате студентов [7]. Также немаловажно, что подобные системы повышают удовлетворенность студентов обучением и их доверие к онлайн-форматам обучения [15].
Заключение
Цифровое сопровождение лабораторных работ по математической статистике в среде Nomotex продемонстрировало высокую эффективность и целесообразность. Разработанный алгоритм обеспечивает автоматическую генерацию индивидуальных заданий, пошаговую проверку основных результатов расчетов и визуализацию данных, что в совокупности создает богатую интерактивную образовательную среду. Студенты получают возможность учиться на собственных ошибках в режиме реального времени и сразу видеть последствия тех или иных действий – будь то неправильный расчет или верный вывод. По итогам внедрения возросла точность и глубина проработки лабораторных заданий, все участники выполнили работы правильно, полностью реализовав заложенные цели обучения. Преподаватели, в свою очередь, смогли сократить время на проверку и уделить больше внимания анализу типичных затруднений и индивидуальному сопровождению отдельных студентов.
Важно подчеркнуть, что предлагаемая методика легко масштабируется и может быть перенесена на другие разделы курса статистики, а также на другие дисциплины, где лабораторные или практические работы включают расчетные задачи. В частности, планируется разработать аналогичные модули Nomotex для тем: проверка статистических гипотез, регрессионный анализ, элементы теории массового обслуживания и т.д. Кроме того, подобные принципы автоматизированной проверки можно использовать и в рамках регулярных практических занятий, внедряя элементы смарт-тетрадей или интерактивных рабочих листов прямо на лекциях или семинарах.