Тепловое воздействие волны H10 на широкую стенку прямоугольного волновода создает возможность измерения таких параметров как проходящая мощность, длина волны, коэффициент стоячей волны, коэффициент отражения посредством нахождения температуры, выделяемой при прохождении электромагнитной волны [1]. Для измерения всех этих параметров сверхвысокочастотных (СВЧ) трактов необходимо знать картину температурного поля на поверхности широкой стенки волновода, другими словами знать значение температуры в любой ее точке. Для создания более выраженной зависимости мощности, создаваемой электромагнитным полем внутри волновода, от температуры на его поверхности производится замена определенного участка волновода на участок линии передачи с потерями. Такой участок представляет отрезок волновода с фланцами, часть широкой стенки которого заменена на поглощающую стенку (ПС), которая обычно выполняется из материала с высоким удельным сопротивлением (например, константан или нихром).
Взаимосвязь картин температурного поля на поверхности ПС и электромагнитного поля внутри волновода, которая и позволяет выдвинуть предположение о возможности вышеописанных измерений, может быть получена аналитически путем решения уравнения теплопроводности для участка стенки линии передачи, нагреваемого внутренними источниками тепла, распределение которых определяется структурой электромагнитного поля. Это уравнение имеет вид:
(1)
где α - коэффициент теплообмена, K - коэффициент теплопроводности, 
- поверхностная плотность мощности на участке широкой стенки волновода.
Для решения уравнения (1) необходимо явно определить функцию . С учетом отражения от нагрузки и неоднородностей она имеет следующий вид [2]:
(2)
где
,
, 
В этих выражениях H0 - амплитуда магнитного поля; Г - модуль комплексного коэффициента отражения (φ0 - его фаза); kx, ky, k||, k† - волновые числа; σ - удельная проводимость ПС.
Существует ряд методов для решения данного уравнения, такие как метод Фурье, метод преобразования Лапласа, вариационный метод, численный метод и метод конечных интегральных преобразований. Важно отметить, что современное программное обеспечение (например, MATLAB) позволяет без труда решать уравнения данного вида.
На рис. 1 представлены картины распределения температуры и поверхностной плотности мощности по поверхности поглощающей стенки (ПС), полученные в результате решения уравнения теплопроводности численным методом для прямоугольного волновода 120×57 мм, при длине волны 16,5 см, мощности 1 кВт, поглощающей стенки из константана толщиной 20 мкм.
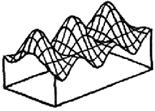
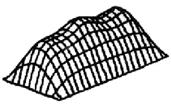
а) распределение плотности мощности б) распределение температуры
Рис. 1. Нагрев широкой стенки волновода волной 
Полученные результаты подтверждают, что температура на поверхности поглощающей стенки волновода однозначно характеризует распределение электромагнитного поля внутри него. Таким образом, появляются возможности создания измерительных устройств, работающих по принципу существующих измерительных линий, для исследования характеристик передаваемых сигналов в СВЧ волноводных трактах.
СПИСОК ЛИТЕРАТУРЫ:
- Гранкин А.С., Лисютченков С.Н., Кузнецов В.Н. Бесконтактный метод измерения параметров СВЧ-сигналов в прямоугольном волноводе, Тр. 5-й регион. конф. Старый Оскол: СТИ МИСиС, 2009. Т. 2.
- Волков В. М. Проектирование средств измерения проходящей мощности: Учеб. Пособие. - Харьков: ХТУРЭ, 2000. - 160 с. ISBN-969-95752-8-1.